高等数学

高等数学（理工科）与数学分析（数学系）实际上讲的是同一块内容。数学分析侧重讲思想与证明，高等数学侧重讲计算。高等数学里概念性的东西如果有疑问，可以去数学分析里找。

初等数学的研究对象基本是不变的量，高等数学的研究对象是变动的量。 而函数关系是变量之间的依赖关系，极限方法是研究变量的一种基本方法。

数学分析

数学分析（英语：mathematical analysis）区别于其他非数学类学生的高等数学内容，是分析学中最古老、最基本的分支，一般指以微积分学、无穷级数和解析函数等的一般理论为主要内容，并包括它们的理论基础（实数、函数、测度和极限的基本理论）的一个较为完整的数学学科。它也是大学数学专业的一门基础课程。[1]

数学分析研究的内容包括实数、复数、实函数及复变函数。数学分析是由微积分演进而来，在微积分发展至现代阶段中，从应用中的方法总结升华为一类综合性分析方法，且初等微积分中也包括许多数学分析的基础概念及技巧，可以认为这些应用方法是高等微积分生成的前提。数学分析的方式和其几何有关，不过只要任一数学空间有定义邻域（拓扑空间）或是有针对两物件距离的定义（度量空间），就可以用数学分析的方式进行分析。

数学分析又称高级微积分，分析学中最古老、最基本的分支。一般指以微积分学和无穷级数一般理论为主要内容，并包括它们的理论基础（实数、函数和极限的基本理论）的一个较为完整的数学学科。

它的发展由微积分开始，并扩展到函数的连续性、可微分及可积分等各种特性。

数学分析的主要内容是微积分学，微积分学的理论基础是极限理论，极限理论的理论基础是实数理论。

数学分析的研究对象是函数，它从局部和整体这两个方面研究函数的基本形态，从而形成微分学和积分学的基本内容。

数学分析的基本方法是极限的方法，或者说是无穷小分析。

数学分析分支领域

数学分析在当前被分为以下几个分支领域：

• 实分析是数学分析中，专门处理实数及实值函数的一个分支[5][6]。这包括对极限、微分、积分、幂级数和测度的研究。
• 复分析，是对从复平面到复平面的复数可微函数的研究，和复数的解析函数（或亚纯函数）有密切的关系。可以应用在许多不同的数学领域中，包括代数几何、数论、应用数学等，也广为应用在物理领域中，例如流体力学、热力学、机械工程、电机工程及量子场论。
• 泛函分析探讨函数空间及一些和向量空间相关的结构（例如内积、范数及拓扑空间）等，以及在作用在这些空间中的线性算子[7][8]，也会介绍例如巴拿赫空间以及希尔伯特空间的概念。
• 傅立叶分析研究如何将一个函数或者信号表达为基本波形的叠加，并扩展成傅立叶级数和傅立叶变换的概念。
• 微分方程是未知数为一变数或多变数的函数，且方程和函数其导数或高阶导数有关的方程[9][10][11]。微分方程在工程、物理、经济、生物学中都是重要的一部分。
• 数值分析是研究数学分析中相关问题（和离散数学不同）中有关数值近似（和符号运算不同）算法的研究。[12]。许多问题的解析解是很难求得的，数值分析不在意解析解，比较著重在可接受的误差范围内找到近似解。

学科代码：34 数学分析▪ 3410:微分学▪ 3420:积分学▪ 3430:级数论▪ 3499:数学分析其他学科

空间

参考：网易公开课：上海交通大学公开课：数学之旅：函数空间 参考：https://zhuanlan.zhihu.com/p/42381836 参考：https://www.jianshu.com/p/42593a412339 参考：https://www.bilibili.com/read/cv3843646/

数学空间

空间即为点的集合

在空间里 原点, 基 这两个东西最重要. 原点就是坐标完全为0的一个点, 基为定义这个空间最基础的“方向”。以二维平面直角坐标系为例，O就是原点, 而 i, j 就是这个空间的两个基。空间中的任意点都可以表示为\(P = a \boldsymbol i + b \boldsymbol j\)，所有可能的权重\((a,b)\)代入上述关系式中，可以得到关于a,b的点集\({a \boldsymbol i + b \boldsymbol j}\)

基其实不要求正交，但不能平行（平行的话相当于少了一条基）

假设有n个不平行的基\(\boldsymbol \varphi_n\)，那么这组基张成的空间中的任意一点为\(P = \Sigma_{i= 1}^n a_i \varphi_i\)。这个空间是里面所有点的点集。

实空间和复空间都是1维的，线性空间是n维的。

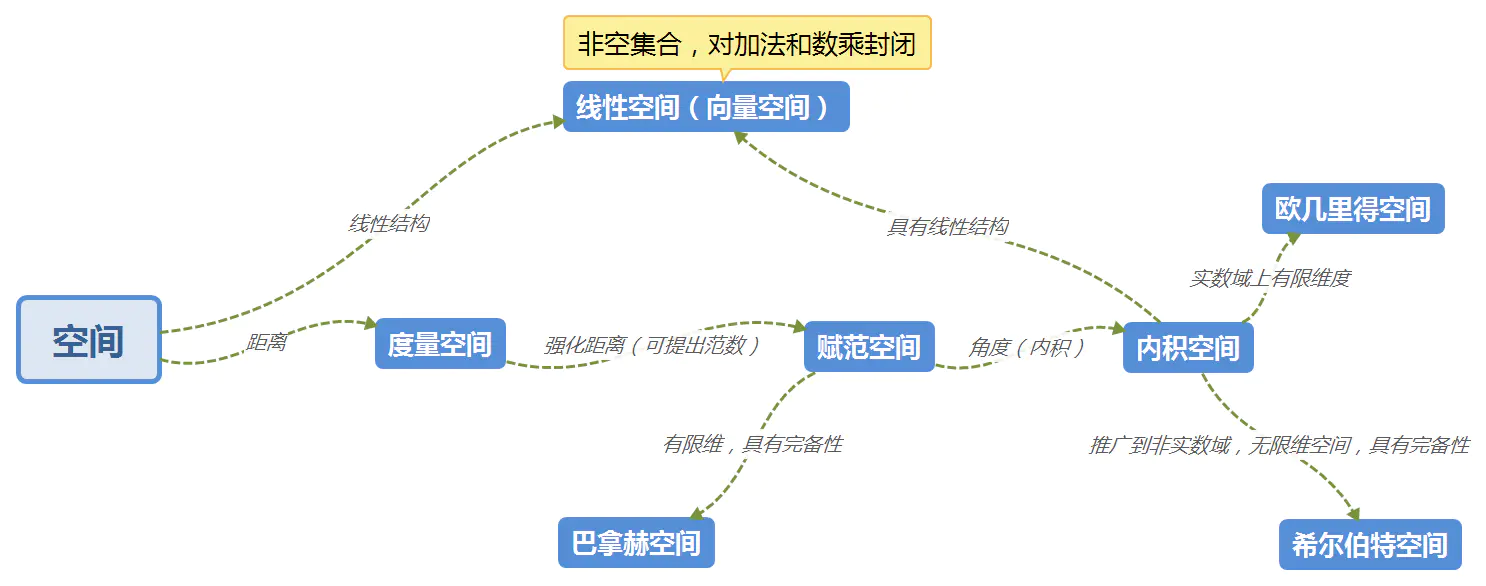
数学的空间：研究工作的对象（元素）和遵循的规则（结构）。 （线性结构：加法和数乘；拓扑结构：距离、范数、开集）

距离的定义：（抽象出必要的属性出来）： 非负、有对称性d(x,y)=d(y,x)、三角不等关系

线性结构的定义： 向量的加法、数乘 （内运算和外运算） 满足（八条规则）：加法的交换率、结合率、零元、负元；数乘的交换律、单位1；数乘与加法的结合率

函数集中的任意两点，有一个内运算、一个外运算，满足八条规则，这样的空间叫做线性空间（线性代数的内容）

范数的定义：（定义强化的距离） 线性空间中的任意两点，距离非负、\(||\alpha x|| = |\alpha|.||x||\)、三角不等关系

内积的定义：（比距离和范数有更深的内涵） 线性空间中的任意两点，有对称性、对第一变元的线性性、正定性（非负性）

拓扑空间：（范围更宽松：连续的概念不需要内积，甚至不需要距离） 用开集定义连续：对任意\(\forall \epsilon, \exist \delta, st. ...\)

函数空间

所谓的函数空间就是 “使用函数作为基的空间”

函数空间是函数的集合。数学上，函数空间指的是从集合 X 到集合 Y 的给定种类的函数的集合。

\(f(x)=\sum_{i=1}^n a_{n} \varphi_{n}(x)\)

函数空间的讨论，在泛函分析中。

注：泛函分析（英语：Functional Analysis）是现代数学分析的一个分支，隶属于分析学，其研究的主要对象是函数构成的函数空间。泛函分析历史根源是由对函数空间的研究和对函数的变换（如傅立叶变换等）的性质的研究。这种观点被证明是对微分方程和积分方程的研究中特别有用。