最优化问题总结
最优化问题总结
最优化问题概述
参考:https://zhuanlan.zhihu.com/p/22801652
最优化问题的引出
以下都是最优化问题的例子: 上班怎么选择乘车路线,才能舒服又快速的到达公司;旅游如何选择航班和宾馆,既省钱又能玩的开心; 跳槽应该选择哪家公司,钱多、事少、离家近,前台妹子颜值高;买房子应该选在哪里,交通发达有学区,生活便利升值快。
可以看出,上面所有的问题都面临无数的选择, 我们会根据自己的偏好对每个选择打一个不同的分数,再从所有的选择中找出最优的一个。这个寻求最优解的过程其实就是最优化问题。
我们要打的分数就称为目标函数。
最优化问题往往还要面临一定的约束条件,比如对旅行路线的选择,总花费和出发、到达时间就构成了约束条件,对买房子的选择,离公司的路程、总价也可能构成约束条件。我们选择的最优解也必须满足这些约束条件。
最优化问题的定义
最优化问题就可以定义为: 在给定的约束条件下, 选择最优的参数和方案,来使得目标函数最大化/最小化的问题。
最优化问题的数学形式是:

这里可以看到最优化问题的三个基本要素:
- 目标函数: 用来衡量结果的好坏
- 参数值:未知的因子,需要通过数据来确定。
- 约束条件:需要满足的限制条件
最优化问题的分类
按约束条件分类
根据约束条件的种类,最优化问题可以分成以下种类:
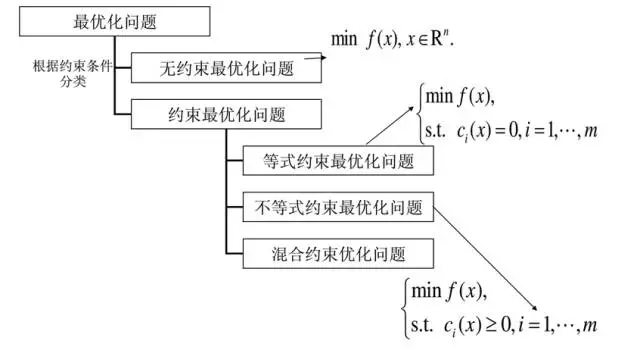
按目标函数分类
而根据目标函数的状态, 最优化问题又可以分成:

按解法分类(解法的选择)
在实际的工作中,我们如何来选择最优化问题的解法呢?
基本的依据有以下几点:
- 目标函数是否连续可导
- 目标函数的形式,是否为线性函数或者二次函数

对应上图:
- 离散最优化方法: 主要用于求解目标函数不连续或者不可导的情况,典型的解法有爬山法、模拟退火、遗传算法和蚁群算法等。
- 线性规划和二次规划:运筹学的重要研究内容,适用于目标函数是线性或二次函数的形式。
- 连续最优化方法: 适用于逻辑回归、SVM、神经网络等机器学习问题,主要方法包括梯度下降、牛顿法和拟牛顿法。
离散最优化
参考:百度百科:整数规划 参考:知乎:运筹学发展概况(上) 参考:知乎:运筹学发展概况(中)
最优化问题似乎自然地分成两类:一类是连续变量的问题,另一类是离散变量的问题。具有离散变量的问题,我们称它为组合的(和离散最优化、整数规划常常混用,实际上范围稍稍有点不同)。在连续变量的问题里,一般地是求一组实数,或者一个函数;在组合问题里,是从一个无限集或者可数无限集里寻找一个对象——典型地是一个整数,一个集合,一个排列,或者一个图。一般地,这两类问题有相当不同的特色,并且求解它们的方法也是很不同的。
整数优化
数规划是指规划中的变量(全部或部分)限制为整数
包括组合优化、0-1优化。。。
而组合最优化通常都可表述为整数规划问题。
组合优化
参考:组合优化百度百科 参考:知乎:离散/整数/组合/非凸优化概述及其在AI的应用
组合优化是20 世纪60 年代逐渐发展起来的一个交叉学科分支,它的研究对象是有限集合上的极值问题。
组合优化与图论、组合学、数理逻辑等有密切关系,在计算机科学、信息科学、管理科学和生命科学等学科有广泛的应用。
组合优化的一个理论基础是计算复杂性理论(NP-完备理论),据此组合优化可以分为两类:P-问题类和NP-难问题类;属于前者的问题有多项式时间算法,属于后者的问题一般认为不存在多项式时间算法,通常采用穷举法、启发式算法和近似算法等方法求解。
通俗的讲,我把组合优化理解为,在组合优化种可能性里找出最优的方案。组合优化是整数规划的子集。的确,绝大多数组合优化问题都可以被建模成(混合)整数规划模型来求解。但是似乎学术圈更多地把组合优化与图(Graph)优化以及网络流(Network Flow)优化联系在一起,并且最终目标不在精确解,而是近似解。
一个组合优化问题由3 部分构成:已知条件的输入,可行解的描述,目标函数的定义。
经典的组合优化问题包括网络流、旅行商、排序、装箱、着色、覆盖、最短网络等等。
NP-完备理论
参考:https://www.ixueshu.com/download/f21b7d05519c59112c66aded1d019c63318947a18e7f9386.html 参考:https://zhuanlan.zhihu.com/p/143003261 参考:https://blog.csdn.net/weixin_42528077/article/details/82779896
计算复杂性理论,又称NP-完备理论。
在计算机领域,组合优化就是要找到适用于计算机的计算方法,这样的方法就是算法。
在数值计算理论可知,当变量的个数增加时,多项式函数比指数函数增加的速度慢很多。基于这个事实,人们认为只有计算复杂性是多项式函数的(精确的)算法才是有效的算法。
在理论计算机科学中,人们把具有有效算法的问题称为P类问题(polynomial)。
P 问题(easy to find)
all problems solvable, deterministically, in polynomial time 译:多项式时间内可解决的问题(当然在多项式时间是可验证的)
NP 问题(esay to check)
non-deterministic Polynomial time 译:非确定性多项式时间可解决的问题
举几个例子来加深印象:
计算1-1000的连续整数之和:这个问题就比较简单,无论是编程还是使用高斯求和公式都可以在有限可接受的时间内完成,这种算是P类问题。
计算地球上所有原子个数之和:这个问题就很困难甚至无解,但是现在有个答案是300个,显然是错的,所以很容易验证但不容易求解,这种算NP类问题。
看到这里我们get了一个非常重要的概念(敲黑板划重点):P类问题是可以在多项式时间内解决并验证的一类问题,NP类问题是可以多项式时间验证但是不确定能否在多项式时间内解决的一类问题。
多项式时间
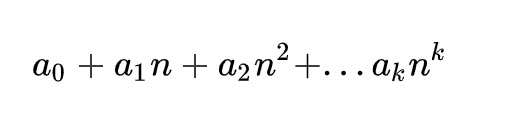
“约化”的概念
- 问题A可以约化为问题B:可以采用解决问题B的方法解决问题A;或者说,问题A可以转化为问题B。(如:一元二次方程的解法可以用来解一元一次方程,只要令二次项系数a=0即可)
- 问题A可以约化为问题B 的直观意义:B的时间复杂度高于或者等于A的时间复杂度。也就是说,问题A不比问题B难。
- 约化具有传递性:如果问题A可约化为问题B,问题B可约化为问题C,则问题A一定可约化为问题C。
- 约化的标准概念:如果能找到这样一个变化法则(要求该变化法则为至多多项式时间复杂度),对任意一个程序A的输入,都能按这个法则变换成程序B的输入,使两程序的输出相同,那么我们说,问题A可约化为问题B。
NP-完全问题(NPC问题)
一个问题约化为另一个问题,时间复杂度增加了,问题的应用范围也增大了。通过对某些问题的不断约化,我们能够不断寻找复杂度更高,但应用范围更广的算法来代替复杂度虽然低,但只能用于很小的一类问题的算法。
如果从某一个NP问题开始不断向上约化,不断找到能“通吃”若干小NP问题的一个稍复杂的大NP问题,那么最后是否有可能找到一个时间复杂度最高,并且能“通吃”所有的 NP问题的这样一个超级NP问题?
NPC问题:存在这样一个NP问题,所有的NP问题都可以约化成它。这种问题不只一个,它有很多个,它是一类问题。这一类问题就是NPC 问题。
NPC问题的定义:同时满足下面两个条件的问题就是NPC问题:首先,它得是一个NP问题;然后,所有的NP问题都可以约化到它。
NPC问题的证明:先证明它至少是一个NP问题,再证明其中一个已知的NPC问题能约化到它(由约化的传递性,则NPC问题定义的第二条也得以满足)
NP-hard问题
NP-hard问题满足NPC问题定义的第二条而不满足第一条。NP-hard问题的范围比NP问题要广。
NP-hard问题同样难以找到多项式时间复杂度的算法,但它也不一定是NP问题(只是所有的NP问题都可以约化到它)。