概率论与数理统计-数理统计-假设检验

除了对总体的参数的估计外，统计推断的另一类重要问题是假设检验问题。 在总体的1）分布函数完全未知或2）只知其形式、但不知其参数的情况，为了推断总体的某些未知特性，提出某些关于总体的假设。 例如，提出总体服从泊松分布的假设，又如，对于正态总体提出数学期望等于\(\mu_{0}\)的假设等。 我们要根据样本对所提出的假设作出是接受，还是拒绝的决策，假设检验是作出这一决策的过程。这里，先结合例子来说明假设检验的基本思想和做法。

假设检验

假设检验的引入

例子

例 1 某车间用一台包装机包装葡萄糖. 袋装糖的净重是一个随机变量,它 服从正态分布. 当机器正常时,其均值为 0.5 kg,标准差为 0.015 kg. 某日开工后为检验包装机是否正常,随机地抽取它所包装的糖 9 袋,称得净重为 \((\mathrm{kg})\)： \(\begin{array}{llllllll}0.497 & 0.506 & 0.518 & 0.524 & 0.498 & 0.511 & 0.520 & 0.515 & 0.512\end{array}\) 问机器是否正常?

也就是问，根据抽取的样本，可不可以判断正态总体\(X \sim N\left(\mu, \sigma^{2}\right)\) 的分布为\(X\sim N(0.5,0.015^2)\)? 这里以 \(\mu, \sigma\) 分别表示这一天袋装糖的净重总体 \(X\) 的均值和标准差. 由于长期实践表明标准差比较稳定,我们就设 \(\sigma=0.015 .\) （也就是作了简化，只检验均值）。 于是 \(X \sim N\left(\mu, 0.015^{2}\right),\) 这里 \(\mu\) 未 知. 问题是根据样本值来判断 \(\mu=0.5\) 还是 \(\mu \neq 0.5 .\) 为此,我们提出两个相互对立的假设\(H_{0}: \mu=\mu_{0}=0.5\)和\(H_{1}: \mu \neq \mu_{0}\) 然后,我们给出一个合理的法则，根据这一法则，利用已知样本作出决策： 是接受假设 \(H_{0}\) (即拒绝假设 \(H_{1}\) ) ,还是拒绝假设 \(H_{0}\) (即接受假设 \(H_{1}\) ). 如果作出的决策是接受 \(H_{0},\) 则认为 \(\mu=\mu_{0}\), 即认为机器工作是正常的,否则，则认为是不正常的.

检验法则的推导过程： 由于要检验的假设涉及总体均值 \(\mu\),故首先想到是否可借助样本均值 \(\bar{X}\) 这 一统计量来进行判断. 我们知道, \(\bar{X}\) 是 \(\mu\) 的无偏估计, \(\bar{X}\) 的观察值 \(\bar{x}\) 的大小在一 定程度上反映 \(\mu\) 的大小. 因此,如果假设 \(H_{0}\) 为真,则观察值 \(\bar{x}\) 与 \(\mu_{0}\) 的偏差 \(\left|\bar{x}-\mu_{0}\right|\) 一般不应太大. 若 \(\left|\bar{x}-\mu_{0}\right|\) 过分大,我们就怀疑假设 \(H_{0}\) 的正确性而拒绝 \(H_{0}\)。 考虑到当 \(H_{0}\) 为真时 \(\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}} \sim N(0,1) .\) 而衡量 \(\left|\bar{x}-\mu_{0}\right|\) 的大小可归结为衡量\(\frac{\left|\bar{x}-\mu_{0}\right|}{\sigma / \sqrt{n}}\) 的大小. 基于上面的想法,我们可适当选定一正数 \(k,\) 使当观察值 \(\bar{x}\) 满足\(\frac{\left|\bar{x}-\mu_{0}\right|}{\sigma / \sqrt{n}} \geqslant k\) 时就拒绝假设 \(H_{0},\) 反之,若 \(\frac{\left|\bar{x}-\mu_{0}\right|}{\sigma / \sqrt{n}}<k,\) 就接受假设 \(H_{0} .\)

然而,由于作出决策的依据是一个样本,当实际上 \(H_{0}\) 为真时仍可能作出拒绝 \(H_{0}\) 的决策(这种可能性是无法消除的)，这是一种错误（弃真错误）,犯这种错误的概率记为 \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\} \quad\) 或 \(\quad P_{\mu_{0}}\left\{\right.\) 拒绝 \(\left.H_{0}\right\} \quad\) 或 \(\quad P_{\mu \in H_{0}}\left\{\right.\) 拒绝 \(\left.H_{0}\right\}\) 或 \(P\left\{\right.\) 拒绝\(H_0\) | 当 \(H_{0}\) 为真时 \(\left.\right\} \quad\)

我们无法排除犯这类错误的可能性,因此自然希望将犯这类错误的概率控制在一定限度之内,即给出一个较小的数 \(\alpha \quad(0<\alpha<1)\),使犯 这类错误的概率不超过 \(\alpha\), 即使得：\(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\} \leqslant \alpha .\)

为了确定常数 \(k,\) 我们考虑统计量 \(\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}} .\) 由于只允许犯这类错误的概率最大为 \(\alpha\),令上面不等式右端取等号,即令： \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\}=P_{\mu_{0}}\left\{\left|\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant k\right\}=\alpha\) 由于当 \(H_{0}\) 为真时 \(, Z=\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}} \sim N(0,1),\) 由标准正态分布分位点的定义得\(k=z_{\alpha / 2}\) 因而,若 \(Z\) 的观察值满足\(|z|=\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant k=z_{a / 2}\)则拒绝 \(H_{0},\) 而若\(|z|=\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right|<k=z_{\alpha / 2}\)则接受 \(H_{0}\).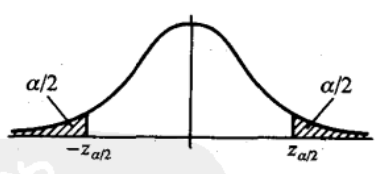

实际推断原理（小概率事件原理）与反证法思想

小概率事件原理：认为概率很小的事件在一次试验中时不会发生的。由此，如果小概率事件发生了，我们就认为发生了不合理的现象。

上例中所采用的检验法则是符合实际推断原理的. 因通常 \(\alpha\) 总是取得较小，一般取 \(\alpha=0.01,0.05 .\) 因而若 \(H_{0}\) 为真, 即当 \(\mu=\mu_{0}\) 时 \(,\left\{\left|\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant z_{\alpha / 2}\right\}\) 是一个小概率事件, 根据实际推断原理,就可以认为,如果 \(H_{0}\) 为真,则由一次试验得到 的观察值 \(\bar{x},\) 满足不等式 \(\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant z_{a / 2}\) 几乎是不会发生的. 现在在一次观察中竟然出现了满足 \(\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant z_{\alpha / 2}\) 的 \(\bar{x},\) 则我们有理由怀疑原来的假设 \(H_{0}\) 的正确性，因而拒绝 \(H_{0} .\) （也运用反证法的思想） 若出现的观察值 \(\bar{x}\) 满足 \(\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right|<z_{\alpha / 2},\) 此时没有理由拒绝假设\(H_{0},\) 因此只能接受假设 \(H_{0} .\)

假设检验问题

前面的检验问题通常叙述成: 在显著性水平 \(\alpha\) 下,检验假设\(H_{0}: \mu=\mu_{0}, \quad H_{1}: \mu \neq \mu_{0}\) 也常说成 “在显著性水平 \(\alpha\) 下,针对 \(H_{1}\) 检验 \(H_{0}\)” . \(H_{0}\) 称为原假设或零假设 \(, H_{1}\) 称为备择假设(意指在原假设被拒绝后可供选择的假设).

开始=>start: 开始
结束=>end: 结束
提出假设=>operation: 提出假设 H0,H1
取定显著性水平=>operation: 取定显著性水平α
选取检验统计量=>operation: 选取检验统计量（分布）
检验（检验法则）=>subroutine: 检验（检验法则）
开始->提出假设->取定显著性水平->选取检验统计量->检验（检验法则）->结束

substart=>start: 检验开始（检验法则）
subend=>end: 结束检验
检验统计量的值在拒绝域=>condition: 检验统计量的值在显著性水平α确定的拒绝域？
拒绝H0（接受H1）=>operation: 拒绝H0（接受H1）
拒绝H1（接受H0）=>operation: 拒绝H1（接受H0）
substart->检验统计量的值在拒绝域(yes)->拒绝H0（接受H1）->subend
substart->检验统计量的值在拒绝域(no)->拒绝H1（接受H0）->subend

显著性水平\(\alpha\)

在前面的例子中，我们看到当样本容量固定时,选定 \(\alpha\) 后,数 \(k\) 就可以确定， 然后按照统计量 \(Z=\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}}\) 的观察值的绝对值 \(|z|\) 大于等于 \(k\) 还是小于 \(k\) 来作出决策. 数 \(k\) 是检验上述假设的一个门槛值. 如果 \(|z|=\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant k,\) 则称 \(\bar{x}\) 与 \(\mu_{0}\)的差异是显著的,这时拒绝 \(H_{0}\); 反之, 如果 \(|z|=\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right|<k,\) 则称 \(\bar{x}\) 与 \(\mu_{0}\) 的差异是不显著的,这时接受 \(H_{0}\). 数 \(\alpha\) 称为（差异的）显著性水平,上面关于 \(\bar{x}\) 与 \(\mu_{0}\) 有无显著差异的判断是在显著性水平 \(\alpha\) 之下作出的.

检验统计量

统计量 \(Z=\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}}\) 称为检验统计量.

假设检验的类别

形如\(H_{0}: \mu=\mu_{0}, \quad H_{1}: \mu \neq \mu_{0}\)中的备择假设 \(H_{1},\) 表示 \(\mu\) 可能大于 \(\mu_{0},\) 也可能小于 \(\mu_{0}\),称为双边备择假设,而称形如\(H_{0}: \mu=\mu_{0}, \quad H_{1}: \mu \neq \mu_{0}\)的假设检验为双边假设检验.

有时,我们只关心总体均值是否增大,例如,试验新工艺以提高材料的强度. 这时,所考虑的总体的均值应该越大越好. 如果我们能判断在新工艺下总体均值 较以往正常生产的大,则可考虑采用新工艺. 此时，我们需要检验（右边）假设\(H_{0}: \mu \leqslant \mu_{0}, \quad H_{1}: \mu>\mu_{0}\)，这样的假设检验,称为右边检验.

类似的，有时候我们需要检验（左边）假设\(H_{0}: \mu \geqslant \mu_{0}, \quad H_{1}: \mu<\mu_{0}\)，这样的假设检验,称为左边检验.

拒绝域

在前面的例子中，是在假设\(H_{0}: \mu=\mu_{0}=0.5\)和\(H_{1}: \mu \neq \mu_{0}\)下的假设检验， 若 \(Z\) 的观察值满足\(|z|=\left|\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}}\right| \geqslant k=z_{a / 2}\)则拒绝 \(H_{0},\) 即\(\bar{x} \geqslant \mu_{0}+\frac{\sigma}{\sqrt{n}} z_{\alpha/2}\)或\(\bar{x} \leqslant \mu_{0}-\frac{\sigma}{\sqrt{n}} z_{\alpha/2}\) 这两个区间称为拒绝域。（双边假设检验的拒绝域）

还可以讨论单边假设检验的拒绝域： 设总体 \(X \sim N\left(\mu, \sigma^{2}\right), \mu\) 未知、 \(\sigma\) 为已知 \(, X_{1}, X_{2}, \cdots, X_{n}\) 是来自 \(X\) 的样本. 给 定显著性水平 \(\alpha .\) 我们来求检验问题 \(H_{0}: \mu \leqslant \mu_{0}, \quad H_{1}: \mu>\mu_{0}\)的拒绝域。 因 \(H_{0}\) 中的全部 \(\mu\) 都比 \(H_{1}\) 中的 \(\mu\) 要小,当 \(H_{1}\) 为真时,观察值 \(\bar{x}\) 往往偏大， 因此,拒绝域的形式为\(\bar{x} \geqslant k \quad(k\) 是某一正常数 \() .\) 下面来确定常数 \(k\) ， \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\}=P_{\mu \in H_{0}}\{\bar{X} \geqslant k\}\) \[ \begin{array}{l} =P_{\mu \leqslant \mu_{0}}\left\{\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}} \geqslant \frac{k-\mu_{0}}{\sigma / \sqrt{n}}\right\} \\ \leqslant P_{\mu \leqslant \mu_{0}}\left\{\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \geqslant \frac{k-\mu_{0}}{\sigma / \sqrt{n}}\right\} \end{array} \] \(\left(\right.\) 上式不等号成立是由于 \(\mu \leqslant \mu_{0}, \frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \geqslant \frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}},\) 事件 \(\left\{\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}} \geqslant \frac{k-\mu_{0}}{\sigma / \sqrt{n}}\right\} \subset\left\{\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \geqslant\right.\)\(\left.\left.\frac{k-\mu_{0}}{\sigma / \sqrt{n}}\right\}\right) .\) \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\} \leqslant \alpha,\) 只需令\(P_{\mu \leqslant \mu_{0}}\left\{\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \geqslant \frac{k-\mu_{0}}{\sigma / \sqrt{n}}\right\}=\alpha\)， 又由于 \(\frac{\bar{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1)\)， \(\frac{k-\mu_{0}}{\sigma / \sqrt{n}}=\)\(\boldsymbol{z}_{\boldsymbol{\alpha}}\)，\(k=\mu_{0}+\frac{\sigma}{\sqrt{n}} z_{a}\)， 即得此右边检验的拒绝域为\(\bar{x} \geqslant \mu_{0}+\frac{\sigma}{\sqrt{n}} z_{a}\) 即\(z=\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}} \geqslant z_{\alpha}\)

同理可得左边检验问题\(H_{0}: \mu \geqslant \mu_{0}, \quad H_{1}: \mu<\mu_{0}\)的拒绝域为\(z=\frac{\bar{x}-\mu_{0}}{\sigma / \sqrt{n}} \leqslant-z_{\alpha}\)

显著性检验

在确定检验法则时,我们应尽可能使犯两类错误的概率都较小.但是， 进一步讨论可知,一般来说,当样本容量固定时,若减少犯一类错误的概率,则犯 另一类错误的概率往往增大. 若要使犯两类错误的概率都减小,除非增加样本容 量.

在给定样本容量的情况下，一般来说,我们总是控制犯第 I 类错误的概率,使 它不大于 \(\alpha .\) 即\(P\left\{\text{当}H_{0}\text{为真时拒绝}H_{0}\right\} =\) \(P_{\mu \in H_{0}}\left\{\text{拒绝}H_{0}\right\} \leqslant \alpha\) \(\alpha\) 的大小视具体情况而定，通常 \(\alpha\) 取 0.1,0.05,0.01,0.005 等值. 这种只对犯第 I 类错误的概率加以控制，而不考虑犯第 II 类错误的概率的检验,称 为显著性检验.

在进行显著性检验时,犯第 I 类错误的概率是由我们控制的. \(\alpha\) 取得小,则概率 \(P\left\{\right.\) 当 \(H_{0}\)为真拒绝 \(\left.H_{0}\right\}\) 就小,这保证了当 \(H_{0}\) 为真时错误地拒绝 \(H_{0}\) 的可能性很小. 这意味着 \(H_{0}\) 是受到保护的,也表明 \(H_{0}, H_{1}\) 的地位不是对等的.于是,在一对对立假设中,选哪一个作为 \(H_{0}\) 需要小心・ 例如,考虑某种药品是否为真,这里可能犯两种错误 : （1）将假药误作为真药，冒着伤害病人的健康甚至生命的风险； （2）将真药误作为假药，则冒着造成经济损失的风险. 显然,犯错误( 1 ) 比犯 错误 (2) 的后果严重, 因此,我们选取“ \(H_{0}\) : 药品为假, \(H_{1}\) : 药品为 真”,即是使得犯第 I 类错误“当药品为假时错判药品为真”的概率\(\leqslant \alpha\). 就是说，选择 \(H_{0}, H_{1}\)使得两类错误中后果严重的错误成为第 I 类错误. 这是选择 \(H_{0}, H_{1}\) 的一个原则 \(.\)

如果在两类错误中,没有一类错误的后果严重更需要避免时,常常取 \(\mathrm{H}_{0}\) 为维持现状, 即取 \(H_{0}\) 为“无效益”、无改进”、无价值”等等・ 例如，取 \(H_{0}\) :新技术未提高效益， \(H_{1}\) :新技术提高效益. 实际上,我们感兴趣的是 \(H_{1}\) “提高效益”,但对采用新技术应持慎重态度. 选取 \(H_{0}\) 为“新技术未提高效益”,一旦 \(H_{0}\) 被拒绝了,表示有较强的理由去采用新技术

在实际问题中,情况比较复杂，如何选取 \(H_{0} 、 H_{1}\) 只能在实践中积累经验,根据实际情况去判断了.

检验（检验方法/检验法则）

选取合适的检验统计量，将样本与假设的偏差归结为一个常见的标准化分布。 取定合适的（错误）显著性水平，若检验统计量的值落到了显著性水平确定的拒绝域之内，就拒绝原假设，否则接受原假设。

我们要进行的工作是， 根据样本,按上述检验方法作出决策在 \(H_{0}\) 与 \(H_{1}\) 两者之间接受其一.

决策（接受或拒绝）

根据样本,按上述检验方法作出决策在 \(H_{0}\) 与 \(H_{1}\) 两者之间接受其一：接受\(H_0\)（同时拒绝\(H_1\)），或者接受\(H_1\)（同时拒绝\(H_0\)）

当检验统计量取某个区域 \(C\) 中的值时,我们拒绝原假设 \(H_{0}\),则称区域 \(C\) 为 拒绝域,拒绝域的边界点称为临界点. 如在上例中拒绝域为 \(|z| \geqslant z_{\alpha / 2},\) 而 \(z=\) \(-z_{a / 2}, z=z_{\alpha / 2}\) 为临界点.

错误决策

由于检验法则是根据样本作出的,总有可能作出错误的决策.

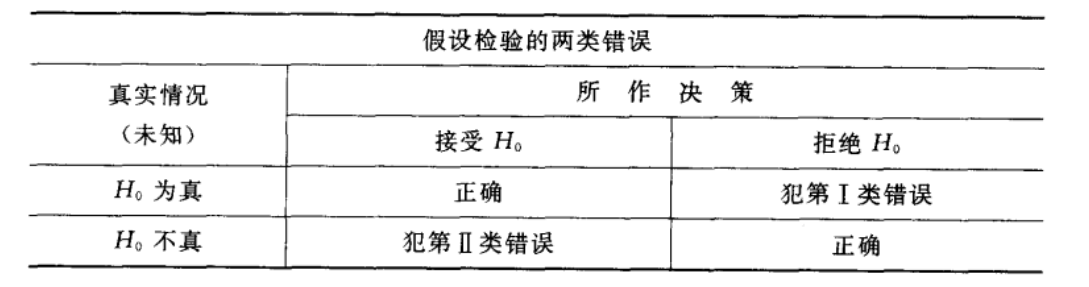
如上面所说的那样,在假设 \(H_{0}\) 实际上为真时,我们可能犯拒绝 \(H_{0}\) 的错误,称这类“弃真”的 错误为第 I 类错误. 又当 \(H_{0}\) 实际上不真时,我们也有可能接受 \(H_{0} .\) 称这类“取伪”的错误为第 II 类错误. 犯第 I 类错误的概率记为\(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\} \quad\) 或 \(\quad P_{\mu_{0}}\left\{\right.\) 拒绝 \(\left.H_{0}\right\} \quad\) 或 \(\quad P_{\mu \in H_{0}}\left\{\right.\) 拒绝 \(\left.H_{0}\right\}\) 或 \(P\left\{\right.\) 拒绝\(H_0\) | 当 \(H_{0}\) 为真时 \(\left.\right\} \quad\) 犯第 II 类错误的概率记为\(P\left\{ H_{0}\right.\) 不真接受 \(\left.H_{0}\right\} \quad\) 或 \(\quad P_{\mu \in H_{1}}\left\{\right.\) 接受 \(\left.H_{0}\right\} .\)

正态总体的均值的假设检验

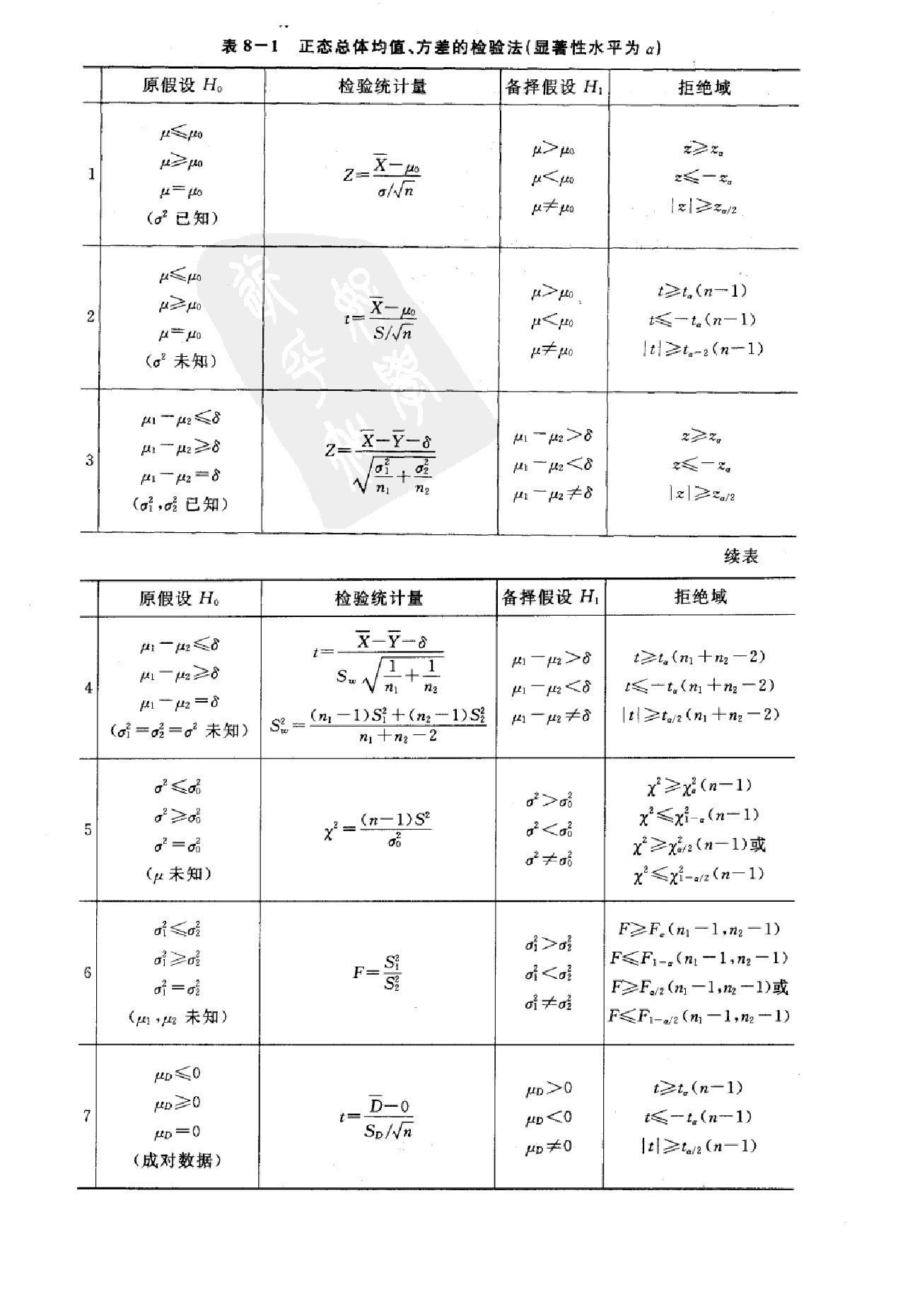
单个总体 \(N\left(\mu, \sigma^{2}\right)\) 均值 \(\mu\) 的检验

\(\sigma^{2}\) 已知,关于 \(\mu\) 的检验 \((Z\) 检验 \()\)

前面的例子（假设检验的引入）中已讨论过正态总体 \(N\left(\mu, \sigma^{2}\right)\) 当 \(\sigma^{2}\) 已知时关于 \(\mu\) 的检验问题, 在这些检验问题中.我们都是利用统计量 \(Z=\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}}\) 来确定拒绝域的. 这种检验法常称为 \(Z\) 检验法.

\(\sigma^{2}\) 未知,关于 \(\mu\) 的检验 \((t\) 检验 \()\)

设总体 \(X \sim N\left(\mu, \sigma^{2}\right),\) 其中 \(\mu, \sigma^{2}\) 未知,我们来求（双边）检验问题\(H_{0}: \mu=\mu_{0}, \quad H_{1}: \mu \neq \mu_{0}\)的拒绝域(显著性水平为 \(\alpha\) ). 设 \(X_{1}, X_{2}, \cdots, X_{n}\) 是来自总体 \(X\) 的样本. 由于 \(\sigma^{2}\) 未知,现在不能利用 \(\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}}\)来确定拒绝域了. 注意到 \(S^{2}\) 是 \(\sigma^{2}\) 的无偏估计,我们用 \(S\) 来代替 \(\sigma,\) 采用\(t=\frac{\bar{X}-\mu_{0}}{S / \sqrt{n}}\)作为检验统计量. 当观察值 \(|t|=\left|\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}\right|\) 过分大时就拒绝 \(H_{0},\) 拒绝域的形式为\(|t|=\left|\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}\right| \geqslant k\) 根据统计量的抽样分布章节介绍的性质，当 \(H_{0}\) 为真时, \(\frac{\bar{X}-\mu_{0}}{S / \sqrt{n}} \sim t(n-1),\) 故由\(P\left\{\text { 当 }H_{0}\right.\) 为真拒绝 \(\left.H_{0}\right\}=P_{\mu_{0}}\left\{\left|\frac{\bar{X}-\mu_{0}}{S / \sqrt{n}}\right| \geqslant k\right\}=\alpha\)，得\(k=t_{a / 2}(n-1),\) 即得拒绝域为\(|t|=\left|\frac{\bar{x}-\mu_{0}}{s / \sqrt{n}}\right| \geqslant t_{a / 2}(n-1)\)

对于正态总体 \(N\left(\mu, \sigma^{2}\right),\) 当 \(\sigma^{2}\) 未知时,关于 \(\mu\) 的单边检验的拒绝域在后面附表中给出。

上述利用 \(t\) 统计量得出的检验法称为 \(t\) 检验法. 在实际中,正态总体的方差常为未知,所以我们常用 \(t\) 检验法来检验关于正 态总体均值的检验问题.

两个正态总体均值差的检验( \(t\) 检验)

两正态总体具有相同方差时

我们还可以用 \(t\) 检验法检验具有相同方差的两正态总体均值差的假设. （一般要先完成两总体的方差相同的假设检验） 设 \(X_{1}, X_{2}, \cdots, X_{n_{1}}\) 是来自正态总体 \(N\left(\mu_{1}, \sigma^{2}\right)\) 的样本 \(, Y_{1}, Y_{2}, \cdots, Y_{n_{2}}\) 是来自正态总体 \(N\left(\mu_{2}, \sigma^{2}\right)\) 的样本,且设两样本独立. 又分别记它们的样本均值为 \(\bar{X}, \bar{Y},\) 记样本 方差为 \(S_{1}^{2}, S_{2}^{2} .\) 设 \(\mu_{1}, \mu_{2}, \sigma^{2}\) 均为未知,要特别引起注意的是,在这里假设两总体 的方差是相等的. 现在来求检验问题:\(H_{0}: \mu_{1}-\mu_{2}=\delta, \quad H_{1}: \mu_{1}-\mu_{2} \neq \delta\)的拒绝域 \((\delta\) 为已知常数) . 取显著性水平为 \(\alpha\).

引用下述 \(t\) 统计量作为检验统计量： \(t=\frac{(\bar{X}-\bar{Y})-\delta}{S_{w} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}}\) 其中\(S_{w}^{2}=\frac{\left(n_{1}-1\right) S_{1}^{2}+\left(n_{2}-1\right) S_{2}^{2}}{n_{1}+n_{2}-2}, S_{w}=\sqrt{S_{w}^{2}}\) 当 \(H_{0}\) 为真时，由统计量的抽样分布章节介绍的性质，有\(t \sim t\left(n_{1}+n_{2}-2\right) .\) 与单个总体的 \(t\) 检验法相仿,其拒绝域的形式为\(\left|\frac{(\bar{x}-\bar{y})-\delta}{s_{w} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}}\right| \geqslant k\) 由\(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\}=P_{\mu_{1}-\mu_{2}=\delta}\left\{\left|\frac{(\bar{X}-\bar{Y})-\delta}{S_{w} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}}\right| \geqslant k\right\}=\alpha\)， 可得可得 \(k=t_{a / 2}\left(n_{1}+n_{2}-2\right) .\) 于是得拒绝域为\(|t|=\frac{|(\bar{x}-\bar{y})-\delta|}{s_{w} \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}} \geqslant t_{a / 2}\left(n_{1}+n_{2}-2\right)\)

两正态总体方差已知时

当两个正态总体的方差均为已知(不一定相等)时,我们可用 \(Z\) 检验法来检验两正态总体均值差的假设问题,见后面附表。

基于成对数据的检验 \((t\text{检验})\)

有时为了比较两种产品、两种仪器、两种方法等的差异,我们常在相同的条 件下做对比试验,得到一批成对的观察值. 然后分析观察数据作出推断. 这种方法常称为逐对比较法.

例子 有两台光谱仪 \(I_{x}, I_{y}\), 用来测量材料中某种金属的含量,为鉴定它们 的测量结果有无显著的差异,制备了 9 件试块(它们的成分、金属含量、均匀性等 均各不相同)，现在分别用这两台仪器对每一试块测量一次,得到 9 对观察值： 问能否认为这两台仪器的测量结果有显著的差异(取 \(\alpha=0.01\) ) ?

本题中的数据是成对的,即对同一试块测出一对数据. 我们看到一对与另一对之间的差异是由各种因素,如材料成分、金属含量、均匀性等因素引起的. 由于各试块的特性有广泛的差别,就不能将仪器 \(I_{x}\) 对 9 个试块的测量结果 (即 表中第一行)看成是同分布随机变量的观察值 . 因而表中第一行不能看成是一个样本的样本值 . 同样,表中第二行也不能看成是一个样本的样本值 . 再者,对 于每一对数据而言,它们是同一试块用不同仪器 \(I_{x}, I_{y}\) 测得的结果,因此,它们不是两个独立的随机变量的观察值。 综上所述,我们不能用前面介绍的两个正态总体均值差的检验( \(t\) 检验)来作检验。而同一对中两个数据的差异则可看成是仅由这两台仪器性能 的差异所引起的,这样,局限于各对中两个数据来比较就能排除种种其他因素， 而只考虑单独由仪器的性能所产生的影响. 从而能比较这两台仪器的测量结果 是否有显著的差异。

一般,设有 \(n\) 对相互独立的观察结果 \(:\left(X_{1}, Y_{1}\right),\left(X_{2}, Y_{2}\right), \cdots,\left(X_{n}, Y_{n}\right),\) 令\(D_{1}=X_{1}-Y_{1}, D_{2}=X_{2}-Y_{2}, \cdots, D_{n}=X_{n}-Y_{n},\) 则 \(D_{1}, D_{2}, \cdots, D_{n}\) 相互独立. 由于 \(D_{1}, D_{2}, \cdots, D_{n}\) 是由同一因素所引起的,可认为它们服从同一分布。 今假设\(D_{i} \sim N\left(\mu_{D}, \sigma_{D}^{2}\right), i=1,2, \cdots, n .\) 这就是说 \(D_{1}, D_{2}, \cdots, D_{n}\) 构成正态总体 \(N\left(\mu_{D}, \sigma_{D}^{2}\right)\)的一个样本,其中 \(\mu_{D}, \sigma_{D}^{2}\) 未知 \(.\) 我们需要基于这一样本检验假设: (1) \(\quad H_{0}: \mu_{D}=0, \quad H_{1}: \mu_{D} \neq 0\) (2) \(H_{0}: \mu_{D} \leqslant 0, \quad H_{1}: \mu_{D}>0\) (3) \(\quad H_{0}: \mu_{D} \geqslant 0, \quad H_{1}: \mu_{D}<0\) 分别记 \(D_{1}, D_{2}, \cdots, D_{n}\) 的样本均值和样本方差的观察值为 \(\bar{d}, s_{D}^{2},\) 按单个正态总体均值的 \(t\) 检验・知检验问题 (1),(2),(3) 的拒绝域分别 为（显著性水平为 \(\alpha\) ) : \(|t|=\left|\frac{\bar{d}}{s_{D} / \sqrt{n}}\right| \geqslant t_{a / 2}(n-1)\) \(t=\frac{\bar{d}}{s_{D} / \sqrt{n}} \geqslant t_{a}(n-1)\) \(t=\frac{\bar{d}}{s_{D} / \sqrt{n}} \leqslant-t_{a}(n-1)\)

正态总体方差的假设检验

单个总体的情况

设总体 \(X \sim N\left(\mu, \sigma^{2}\right), \mu, \sigma^{2}\) 均未知 \(, X_{1}, X_{2}, \cdots, X_{n}\) 是来自 \(X\) 的样本. 要求（双边）检验假设(显著性水平为 \(\alpha\) ): \(H_{0}: \sigma^{2}=\sigma_{0}^{2}, \quad H_{1}: \sigma^{2} \neq \sigma_{0}^{2}\), 其中\(\sigma_{0}^{2}\) 为已知常数. 由于 \(S^{2}\) 是 \(\sigma^{2}\) 的无偏估计,当 \(H_{0}\) 为真时,观察值 \(s^{2}\) 与 \(\sigma_{0}^{2}\) 的比值 \(\frac{s^{2}}{\sigma_{0}^{2}}\) 般来说 应在 1 附近摆动,而不应过分大于 1 或过分小于 \(1 .\) 由统计量的抽样分布章节介绍的性质，当 \(H_{0}\) 为真时，有\(\frac{(n-1) S^{2}}{\sigma_{0}^{2}} \sim \chi^{2}(n-1)\)。 取\(\chi^{2}=\frac{(n-1) S^{2}}{\sigma_{0}^{2}}\)作为检验统计量, 如上所说知道上述检验问题的拒绝域具有以下的形式： \(\frac{(n-1) s^{2}}{\sigma_{0}^{2}} \leqslant k_{1} \quad\) 或 \(\quad \frac{(n-1) s^{2}}{\sigma_{0}^{2}} \geqslant k_{2}\) 此处 \(k_{1}, k_{2}\) 的值由下式确定 : \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\}\) \(=P_{o_{0}^{2}}\left\{\left(\frac{(n-1) S^{2}}{\sigma_{0}^{2}} \leqslant k_{1}\right) \cup\left(\frac{(n-1) S^{2}}{\sigma_{0}^{2}} \geqslant k_{2}\right)\right\}=\alpha\) 为计算方便起见，习惯上取： \(P_{a_{0}^{2}}\left\{\frac{(n-1) S^{2}}{\sigma_{0}^{2}} \leqslant k_{1}\right\}=\frac{\alpha}{2}, P_{o_{0}^{2}}\left\{\frac{(n-1) S^{2}}{\sigma_{0}^{2}} \geqslant k_{2}\right\}=\frac{\alpha}{2}\) 故得 \(k_{1}=\chi_{1^{-} \alpha / 2}^{2}(n-1), k_{2}=\chi_{\alpha / 2}^{2}(n-1) .\) 于是得拒绝域为\(\frac{(n-1) s^{2}}{\sigma_{0}^{2}} \leqslant \chi_{1-a / 2}^{2}(n-1) \quad\) 或 \(\quad \frac{(n-1) s^{2}}{\sigma_{0}^{2}} \geqslant \chi_{\alpha / 2}^{2}(n-1)\)

下面求右边检验问题（显著性水平为 \(\alpha\) )：\(H_{0}: \sigma^{2} \leqslant \sigma_{0}^{2}, \quad H_{1}: \sigma^{2}>\sigma_{0}^{2}\)的拒绝域。 因 \(H_{0}\) 中的全部 \(\sigma^{2}\) 都比 \(H_{1}\) 中的 \(\sigma^{2}\) 要小,当 \(H_{1}\) 为真时, \(S^{2}\) 的观察值 \(s^{2}\) 往往偏大,因此拒绝域的形式为\(s^{2} \geqslant k\) 下面来确定常数 \(k\). \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\}=P_{o^{2} \leqslant_{o}^{2}}\left\{S^{2} \geqslant k\right\}\) \(=P_{o^{2} \leqslant\sigma_{0}^{2}}\left\{\frac{(n-1) S^{2}}{\sigma_{0}^{2}} \geqslant \frac{(n-1) k}{\sigma_{0}^{2}}\right\}\) \(\leqslant P_{\sigma^{2} \leqslant \sigma_{0}^{2}}\left\{\frac{(n-1) S^{2}}{\sigma^{2}} \geqslant \frac{(n-1) k}{\sigma_{0}^{2}}\right\} \quad\left(\right.\) 因为 \(\left.\sigma^{2} \leqslant \sigma_{0}^{2}\right)\) 要控制 \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\} \leqslant \alpha,\) 只需令\(P_{a^{2} \leqslant o_{0}^{2}}\left\{\frac{(n-1) S^{2}}{\sigma^{2}} \geqslant \frac{(n-1) k}{\sigma_{0}^{2}}\right\}=\alpha\) 又因 \(\frac{(n-1) S^{2}}{\sigma^{2}} \sim \chi^{2}(n-1),\) 得 \(\frac{(n-1) k}{\sigma_{0}^{2}}\)\(=\chi_{\alpha}^{2}(n-1)\) 。 于是 \(k=\frac{\sigma_{0}^{2}}{n-1} \chi_{a}^{2}(n-1),\) 得此单边检验问题的拒绝域为 \(s^{2} \geqslant\) \(\frac{\sigma_{0}^{2}}{n-1} \chi_{\sigma}^{2}(n-1),\) 即\(\chi^{2}=\frac{(n-1) s^{2}}{\sigma_{0}^{2}} \geqslant \chi_{a}^{2}(n-1)\)

类似地，可得左边检验问题：\(H_{0}: \sigma^{2} \geqslant \sigma_{0}^{2}, \quad H_{1}: \sigma^{2}<\sigma_{0}^{2}\)的拒绝域： \(\chi^{2}=\frac{(n-1) s^{2}}{\sigma_{0}^{2}} \leqslant \chi_{1-\alpha}^{2}(n-1)\)

以上检验法称为\(\chi^{2}\) 检验法

两个总体的情况

设 \(X_{1}, X_{2}, \cdots, X_{n_{1}}\) 是来自总体 \(N\left(\mu_{1}, \sigma_{1}^{2}\right)\) 的样本 \(, Y_{1}, Y_{2}, \cdots, Y_{n_{2}}\) 是来自总体\(N\left(\mu_{2}, \sigma_{2}^{2}\right)\) 的样本,且两样本独立. 其样本方差分别为 \(S_{1}^{2}, S_{2}^{2} .\) 且设 \(\mu_{1}, \mu_{2}, \sigma_{1}^{2}, \sigma_{2}^{2}\) 均为未知. 现在需要检验假设(显著性水平为 \(\alpha\) )：\(H_{0}: \sigma_{1}^{2} \leqslant \sigma_{2}^{2}, \quad H_{1}: \sigma_{1}^{2}>\sigma_{2}^{2}\)

当 \(H_{0}\) 为真时 \(, E\left(S_{1}^{2}\right)=\sigma_{1}^{2} \leqslant \sigma_{2}^{2}=E\left(S_{2}^{2}\right),\) 当 \(H_{1}\) 为真时 \(E\left(S_{1}^{2}\right)=\sigma_{1}^{2}>\sigma_{2}^{2}=E\left(S_{2}^{2}\right)\). 当 \(H_{1}\) 为真时,观察值 \(\frac{S_{1}^{2}}{S_{2}^{2}}\) 有偏大的趋势,故拒绝域具有形式：\(\frac{s_{1}^{2}}{s_{2}^{2}} \geqslant k\)

常数 \(k\) 确定如下： \(P\left\{\underline{y} H_{0}\right.\) 为真拒绝 \(\left.H_{0}\right\}=P_{o_{1}^{2} \leqslant \sigma_{2}^{2}}\left\{\frac{S_{1}^{2}}{S_{2}^{2}} \geqslant k\right\}\) \(\leqslant P_{o_{1}^{2} \leqslant \sigma_{2}^{2}}\left\{\frac{S_{1}^{2} / S_{2}^{2}}{\sigma_{1}^{2} / \sigma_{2}^{2}} \geqslant k\right\} \quad\left(\right.\) 因为 \(\left.\sigma_{1}^{2} / \sigma_{2}^{2} \leqslant 1\right)\) 要控制 \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\} \leqslant \alpha,\) 只需令\(P_{o_{1}^{2} \leqslant \sigma_{2}^{2}}\left\{\frac{S_{1}^{2} / S_{2}^{2}}{\sigma_{1}^{2} / \sigma_{2}^{2}} \geqslant k\right\}=\alpha\) 再由统计量的抽样分布章节介绍的性质，知 \(\frac{S_{1}^{2} / S_{2}^{2}}{\sigma_{1}^{2} / \sigma_{2}^{2}} \sim F\left(n_{1}-1, n_{2}-1\right),\) 得 \(k=F_{\alpha}\left(n_{1}-1, n_{2}- 1\right)\). 即得检验问题的拒绝域为\(F=\frac{s_{1}^{2}}{s_{2}^{2}} \geqslant F_{a}\left(n_{1}-1, n_{2}-1\right)\)

上述检验法称为 \(F\) 检验法. 关于 \(\sigma_{1}^{2}, \sigma_{2}^{2}\) 的另外两个检验问题的拒绝域在后面附表中给出.

正态总体均值和方差的假设检验汇总

置信区间域假设检验的关系

置信区间与假设检验之间有明显的联系, 先考察置信区间与双边检验之间的对应关系. 设 \(X_{1}, \cdots, X_{n}\) 是一个来自总体的样本 \(, x_{1}, \cdots, x_{n}\) 是相应的样本值, \(\Theta\) 是参数 \(\theta\) 的可能取值范围。 设 \(\left(\underline{\theta}\left(X_{1}, \cdots, X_{n}\right), \bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right)\) 是参数 \(\theta\) 的一个置信水平为 \(1-\alpha\) 的置信区间,则对于任意 \(\theta \in \Theta\),有\(P_{\theta}\left\{\theta\left(X_{1}, \cdots, X_{n}\right)<\theta<\bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right\} \geqslant 1-\alpha\)， 即有\(P_{\theta_{0}}\left\{\left(\theta_{0} \leqslant \theta\left(X_{1}, \cdots, X_{n}\right)\right) \cup\left(\theta_{0} \geqslant \bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right)\right\} \leqslant \alpha\)，

考虑显著性水平为 \(\alpha\) 的双边检验：\(H_{0}: \theta=\theta_{0}, \quad H_{1}: \theta \neq \theta_{0}\)， 按显著性水平为 \(\alpha\) 的假设检验的拒绝域的定义, 双边检验：\(H_{0}: \theta=\theta_{0}, \quad H_{1}: \theta \neq \theta_{0}\)的拒绝域为\(\theta_{0} \leqslant \underline\theta\left(x_{1}, \cdots, x_{n}\right) \quad\) 或 \(\quad \theta_{0} \geqslant \bar{\theta}\left(x_{1}, \cdots, x_{n}\right)\) 接受域为\(\underline\theta\left(x_{1}, \cdots, x_{n}\right)<\theta_{0}<\bar{\theta}\left(x_{1}, \cdots, x_{n}\right)\).

这就是说,当我们要检验假设：\(H_{0}: \theta=\theta_{0}, \quad H_{1}: \theta \neq \theta_{0}\)时,先求出 \(\theta\) 的置信水平为 \(1-\alpha\) 的置信 区间 \((\underline\theta, \bar{\theta}),\) 然后考察区间 \((\theta, \bar{\theta})\) 是否包含 \(\theta_{0},\) 若 \(\theta_{0} \in(\underline\theta, \bar{\theta})\) 则接受 \(H_{0},\) 若 \(\theta_{0} \notin(\underline{\theta},\bar{\theta}),\) 则拒绝 \(H_{0} .\)

反之,对于任意 \(\theta_{0} \in \Theta,\) 考虑显著性水平为 \(\alpha\) 的假设检验问题: \(H_{0}: \theta=\theta_{0}, \quad H_{1}: \theta \neq \theta_{0}\), 假设它的接受域为\(\underline\theta\left(x_{1}, \cdots, x_{n}\right)<\theta_{0}<\bar{\theta}\left(x_{1}, \cdots, x_{n}\right)\) 即有\(P_{\theta_{0}}\left\{\underline\theta\left(X_{1}, \cdots, X_{n}\right)<\theta_{0}<\bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right\} \geqslant 1-\alpha\) 由 \(\theta_{0}\) 的任意性,由上式知对于任意 \(\theta \in \Theta\),有\(P_{\theta}\left\{\underline\theta\left(X_{1}, \cdots, X_{n}\right)<\theta<\bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right\} \geqslant 1-\alpha\), 因此 \(\left(\theta\left(X_{1}, \cdots, X_{n}\right), \bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right)\) 是参数 \(\theta\) 的一个置信水平为 \(1-\alpha\) 的置信区间.

这就是说,为要求出参数 \(\theta\) 的置信水平为 \(1-\alpha\) 的置信区间， 我们先求出显著性水平为 \(\alpha\) 的假设检验问题 \(: H_{0}: \theta=\theta_{0}, H_{1}: \theta \neq \theta_{0}\) 的接受域 \(\underline{\theta}\left(x_{1}, \cdots, x_{n}\right)<\theta_{0}\)\(<\bar{\theta}\left(x_{1}, \cdots, x_{n}\right),\) 那么 \(,\left(\underline{\theta}\left(X_{1}, \cdots, X_{n}\right), \bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right)\) 就是 \(\theta\) 的置信水平为 \(1-\alpha\)的置信区间

还可验证,置信水平为 \(1-\alpha\) 的单侧置信区间 \(\left(-\infty, \bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right)\) 与显著性水平为 \(\alpha\) 的左边检验问题 \(H_{0}: \theta \geqslant \theta_{0}, H_{1}: \theta<\theta_{0}\) 有类似的对应关系. 即若已求得单侧置信区间 \(\left(-\infty, \bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right),\) 则当 \(\theta_{0} \in\left(-\infty, \bar{\theta}\left(x_{1}, \cdots, x_{n}\right)\right)\) 时接受\(H_{0},\) 当 \(\theta_{0} \notin\left(-\infty, \bar{\theta}\left(x_{1}, \cdots, x_{n}\right)\right)\) 时拒绝 \(H_{0} .\) 反之,若已求得检验问题 \(H_{0}: \theta \geqslant \theta_{0},\)\(H_{1}: \theta<\theta_{0}\) 的接受域为 \(-\infty<\theta_{0} \leqslant \bar{\theta}\left(x_{1}, \cdots, x_{n}\right),\) 则可得 \(\theta\) 的一个单侧置信区间\(\left(-\infty, \bar{\theta}\left(X_{1}, \cdots, X_{n}\right)\right)\)

置信水平为 \(1-\alpha\) 的单侧置信区间 \(\left(\theta\left(X_{1}, \cdots, X_{n}\right), \infty\right)\) 与显著性水平为 \(\alpha\) 的右边检验问题 \(H_{0}: \theta \leqslant \theta_{0}, H_{1}: \theta>\theta_{0}\) 也有类似的对应关系. 即若已求得单侧置信区间 \(\left(\theta\left(X_{1}, \cdots, X_{n}\right), \infty\right) .\) 则 当 \(\theta_{0} \in\left(\theta\left(x_{1}, \cdots, x_{n}\right), \infty\right)\) 时接 受 \(H_{0},\) 当 \(\theta_{0} \notin\)\(\left(\theta\left(x_{1}, \cdots, x_{n}\right), \infty\right)\) 时拒绝 \(H_{0} .\) 反之,若已求得检验问题 \(H_{0}: \theta \leqslant \theta_{0}, H_{1}: \theta>\theta_{0}\) 的接受域为 \(\theta\left(x_{1}, \cdots, x_{n}\right) \leqslant \theta_{0}<\infty,\) 则可得 \(\theta\) 的一个单侧置信区间 \(\left(\theta\left(X_{1}, \cdots, X_{n}\right)\right.\),\(\infty)\)

样本容量的选取

以上我们在进行假设检验时，总是根据问题的要求，预先给出显著性水平以控制犯第Ⅰ类错误的概率，而犯第Ⅱ类错误的概率则依赖于样本容量的选择。 在些实际问题中，我们除了希望控制犯第Ⅰ类错误的概率外，往往还希望控制犯第Ⅱ类错误的概率。在这一节，我们将阐明如何选取样本的容量使得犯第Ⅱ类错误的概率控制在预先给定的限度之内。为此，我们引入施行特征函数

//TODO 施行特征函数

分布拟合检验

上面介绍的各种检验法都是在总体分布形式为已知的前提下进行讨论的。 但在实际问题中,有时不能知道总体服从什么类型的分布,这时就需要根据样本来检验关于分布的假设. 本节介绍 \(\chi^{2}\) 拟合检验法. 它可以用来检验总体是否具 有某一个指定的分布或属于某一个分布族,还介绍专用于检验分布是否为正态的“偏度、峰度检验法”

单个分布的 \(\chi^{2}\) 拟合检验法

设总体 \(X\) 的分布未知 \(, x_{1}, x_{2}, \cdots, x_{n}\) 是来自 \(X\) 的样本值. 我们来检验假设: \(H_{0}:\) 总体 \(X\) 的分布函数为 \(F(x) .\) \(H_{1}:\) 总体 \(X\) 的分布函数不是 \(F(x)\) 其中设 \(F(x)\) 不含未知参数. (也常以分布律或概率密度代替 \(F(x))\).

下面来定义检验统计量. 将在 \(H_{0}\) 下 \(X\) 可能取值的全体 \(\Omega\) 分成互不相交的 子集 \(A_{1}, A_{2}, \cdots, A_{k},\) 以 \(f_{i} \quad(i=1,2, \cdots, k)\) 记样本观察值 \(x_{1}, x_{2}, \cdots, x_{n}\) 中落在 \(A_{i}\)的个数,这表示事件 \(A_{i}=\left\{X\right.\) 的值落在子集 \(A_{i}\) 内 \(\}\) 在 \(n\) 次独立试验中发生 \(f_{i}\) 次,于是在这 \(n\) 次试验中事件 \(A_{i}\) 发生的频率为 \(f_{i} / n .\) 另一方面, 当 \(H_{0}\) 为真时， 我们可以根据 \(H_{0}\) 中所假设的 \(X\) 的分布函数来计算事件 \(A_{i}\) 的概率,得到 \(p_{i}=\)\(P\left(A_{i}\right), i=1,2, \cdots, k .\) 频率 \(f_{i} / n\) 与概率 \(p_{i}\) 会有差异,但一般来说,当 \(H_{0}\) 为真,且试验的次数又甚多时,这种差异不应太大,因此 \(\left(\frac{f_{i}}{n}-p_{i}\right)^{2}\)不应太大. 我们采用形如\(\sum_{i=1}^{k} C_{i}\left(\frac{f_{i}}{n}-p_{i}\right)^{2}\)的统计量来度量样本与 \(H_{0}\) 中所假设的分布的吻合程度, 其中 \(C_{i} \quad(i=1,2, \cdots,k)\) 为给定的常数. 皮尔逊证明,如果选取 \(C_{i}=n / p_{i} \quad(i=1,2, \cdots, k),\) 即\(\chi^{2}=\sum_{i=1}^{k} \frac{n}{p_{i}}\left(\frac{f_{i}}{n}-p_{i}\right)^{2}=\sum_{i=1}^{k} \frac{\left(f_{i}-n p_{i}\right)^{2}}{n p_{i}}=\sum_{i=1}^{n} \frac{f_{i}^{2}}{n p_{i}}-n\), 则统计量\(\chi^{2}=\sum_{i=1}^{n} \frac{f_{i}^{2}}{n p_{i}}-n\)具有下述定理中所述的简单性质. 于是我们就采用其作为检验统计量。

定理：若 \(n\) 充分大 \((n \geqslant 50),\) 则当 \(H_{0}\) 为真时统计量近似服\(\chi^{2}=\sum_{i=1}^{n} \frac{f_{i}^{2}}{n p_{i}}-n\)从 \(\chi^{2}(k-1)\)分布.（证略）

据以上的讨论,当 \(H_{0}\) 为真时,\(\chi^{2}=\sum_{i=1}^{n} \frac{f_{i}^{2}}{n p_{i}}-n\)中的 \(\chi^{2}\) 不应太大,如 \(\chi^{2}\) 过分大就拒绝 \(H_{0}\), 拒绝域的形式为\(\chi^{2} \geqslant G \quad(G\) 为正常数 \() .\) 对于给定的显著性水平 \(\alpha,\) 确定 \(G\) 使： \(P\left\{\right.\) 当 \(H_{0}\) 为真时拒绝 \(\left.H_{0}\right\}=P_{H_{0}}\left\{\chi^{2} \geqslant G\right\}=\alpha\). 由上述定理得 \(G=\chi_{\alpha}^{2}(k-1) .\) 即当样本观察值使\(\chi^{2}=\sum_{i=1}^{n} \frac{f_{i}^{2}}{n p_{i}}-n\)式中的 \(\chi^{2}\) 的值有\(\chi^{2} \geqslant \chi_{\alpha}^{2}(k-1)\)， 则在显著性水平 \(\alpha\) 下拒绝 \(H_{0}\);否则就接受 \(H_{0}\). 这就是单个分布的 \(\chi^{2}\) 拟合检验法.

注意：\(\chi^{2}\) 拟合检验法是基于上述定理得到的,所以使用时必须注意 \(n\) 不能小于 \(50 .\) 另 外 \(n p_{i}\) 不能太小,应有 \(n p_{i} \geqslant 5\),否则应适当合并 \(A_{i}\),以满足这个要求。

分布族的 \(\chi^{2}\) 拟合检验

在上面要检验的原假设是 \(H_{0}:\) 总体 \(X\) 的分布函数是 \(F(x),\) 其中 \(F(x)\) 是 已知的,这种情况是不多的.

我们经常遇到的所需检验的原假设是： \(H_{0}:\) 总体 \(X\) 的分布函数是 \(F\left(x ; \theta_{1}, \cdots, \theta_{r}\right),\)其中 \(F\) 的形式已知,而 \(\boldsymbol{\theta}=\left(\theta_{1}, \theta_{2}, \cdots, \theta_{r}\right)\) 是未知参数，它们在某一个范围取值. 在 \(F\left(x ; \theta_{1}, \theta_{2}, \cdots, \theta_{r}\right)\) 中当参数 \(\theta_{1}, \theta_{2}, \cdots, \theta_{r}\) 取不同的值时,就得到不同的分布，因而 \(F\left(x ; \theta_{1}, \theta_{2}, \cdots, \theta_{r}\right)\) 代表一族分布. \(H_{0}\) 表示总体 \(X\) 的分布属于分布族 \(F\left(x ; \theta_{1}, \theta_{2}, \cdots, \theta_{r}\right)\)。 采用类似单个分布的 \(\chi^{2}\) 拟合检验中的方法来定义检验统计量,将在 \(H_{0}\) 下\(X\) 可能取值的全体 \(\Omega\) 分成 \(k \quad(k>r+1)\) 个互不相交的子集 \(A_{1}, A_{2}, \cdots, A_{k},\) 以\(f_{i} \quad(i=1,2, \cdots, k)\) 记样本观察值 \(x_{1}, x_{2}, \cdots, x_{n}\) 落在 \(A_{i}\) 的个数 \(,\) 则事件 \(A_{i}=\{X\)的值落在 \(A_{i}\) 内 \(\}\) 的频率为 \(f_{i} / n .\) 另一方面,当 \(H_{0}\) 为真时,由 \(H_{0}\) 所假设的分布 函数来计算 \(P\left(A_{i}\right),\) 得到\(P\left(A_{i}\right)=p_{i}\left(\theta_{1}, \theta_{2}, \cdots, \theta_{r}\right)=p_{i}(\boldsymbol{\theta})=p_{i} .\) 此时,需先利用样本求出未知参数的最大似然估计 (在 \(H_{0}\) 下 )，以估计值作为参数值,求出 \(p_{i}\)的估计值 \(\hat{p}_{i}=\hat{P}\left(A_{i}\right),\) 在\(\chi^{2}=\sum_{i=1}^{n} \frac{f_{i}^{2}}{n p_{i}}-n\)中以 \(\hat{p}_{i}\) 代替 \(p_{i},\) 取\(\chi^{2}=\sum_{i=1}^{k} \frac{f_{i}^{2}}{n \hat{p}_{i}}-n\)作为检验假设 \(H_{0}\) 的统计量. 可以证明,在某些条件下,在 \(H_{0}\) 为真时近似地有\(\chi^{2}=\sum_{i=1}^{k} \frac{f_{\hat{p}}^{2}}{n \hat{p}_{i}}-n \sim \chi^{2}(k-r-1)\)， 与在单个分布的 \(\chi^{2}\) 拟合检验中中一样， 可得假设检验问题\(H_{0}:\) 总体 \(X\) 的分布函数是 \(F\left(x ; \theta_{1}, \cdots, \theta_{r}\right)\)的拒绝域为\(\chi^{2} \geqslant \chi_{\alpha}^{2}(k-r-1)\)， \(\alpha\) 为显著性水平. 以上就是用来检验分布族的 \(\chi^{2}\) 拟合检验法.

偏度、峰度检验

根据关于中心极限定理的论述知道,正态分布随机变量是较广泛地存在的,因此,当研究一连续型总体时,人们往往先考察它是否服从正态分布. 上面介绍的 \(\chi^{2}\) 拟合检验法虽然是检验总体分布的较一般的方法,但用它来检验总体的正态性时,犯第 II 类错误的概率往往较大. 为此,统计学家们对检验正态总体的种种方法进行了比较,根据奥野忠一等人在 20 世纪 70 年代进行的大量模 拟计的结果,认为正态性检验方法中,总的来说,以“偏度、峰度检验法”及“夏 皮罗一威尔克法”较为有效. 在这里我们仅介绍偏度、峰度检验法.

随机变量 \(X\) 的偏度和峰度指的是 \(X\) 的标准化变量 \([X-E(X)] / \sqrt{D(X)}\) 的 三阶矩和四阶矩: \(\nu_{1}=E\left[\left(\frac{X-E(X)}{\sqrt{D(X)}}\right)^{3}\right]=\frac{E\left[(X-E(X))^{3}\right]}{(D(X))^{3 / 2}}\) \(\nu_{2}=E\left[\left(\frac{X-E(X)}{\sqrt{D(X)}}\right)^{4}\right]=\frac{E\left[(X-E(X))^{4}\right]}{(D(X))^{2}}\)

当随机变量 \(X\) 服从正态分布时 \(, \nu_{1}=0\) 且 \(\nu_{2}=3\).

设 \(X_{1}, X_{2}, \cdots, X_{n}\) 是来自总体 \(X\) 的样本,则 \(\nu_{1}, \nu_{2}\) 的矩估计量分别是\(G_{1}=B_{3} / B_{2}^{3 / 2}, \quad G_{2}=B_{4} / B_{2}^{2}\)

若总体 \(X\) 为正态变量,则可证当 \(n\) 充分大时,近似地有： \(G_{1} \sim N\left(0, \frac{6(n-2)}{(n+1)(n+3)}\right)\) \(G_{2} \sim N\left(3-\frac{6}{n+1}, \frac{24 n(n-2)(n-3)}{(n+1)^{2}(n+3)(n+5)}\right)\)

设 \(X_{1}, X_{2}, \cdots, X_{n}\) 是来自总体 \(X\) 的样本,现在来检验假设： \(H_{0}: X\) 为正态总体.

记\(\sigma_{1}=\sqrt{\frac{6(n-2)}{(n+1)(n+3)}}, \quad \sigma_{2}=\sqrt{\frac{24 n(n-2)(n-3)}{(n+1)^{2}(n+3)(n+5)}}\) \(\mu_{2}=3-\frac{6}{n+1}, U_{1}=G_{1} / \sigma_{1}, U_{2}=\left(G_{2}-\mu_{2}\right) / \sigma_{2} .\) 当 \(H_{0}\) 为真且 \(n\) 充分大时,近似地有\(U_{1} \sim N(0,1), \quad U_{2} \sim N(0,1)\)

可以证明样本偏度 \(G_{1}\) 、样本峰度 \(G_{2}\) 分别依概率收豆于总体偏度 \(\nu_{1}\) 和总体峰度 \(\nu_{2} .\) 因此当 \(H_{0}\) 为真且 \(n\) 充分大时,一般来说 \(, G_{1}\) 与 \(\nu_{1}=0\) 的偏离不应太大,而 \(G_{2}\) 与 \(\nu_{2}=3\) 的偏离不应太大. 故从直观来看当 \(\left|U_{1}\right|\) 的观察值 \(\left|u_{1}\right|\) 或 \(\left|U_{2}\right|\) 的观察值 \(\left|u_{2}\right|\) 过大时就拒绝 \(H_{0} .\) 取显著性水平为 \(\alpha, H_{0}\) 的拒绝域为\(\left|u_{1}\right| \geqslant k_{1} \quad\) 或 \(\quad\left|u_{2}\right| \geqslant k_{2}\) 其中 \(k_{1}, k_{2}\) 由以下两式确定： \(P_{H_{0}}\left\{\left|U_{1}\right| \geqslant k_{1}\right\}=\frac{\alpha}{2}, \quad P_{H_{0}}\left\{\left|U_{2}\right| \geqslant k_{2}\right\}=\frac{\alpha}{2}\) 这里记号 \(P_{H_{0}}\{\bullet\}\) 表示当 \(H_{0}\) 为真时事件 \(\{\bullet\}\) 的概率,即有 \(k_{1}=z_{\alpha / 4}, k_{2}=z_{\alpha / 4} .\) 于是得拒绝域为\(\left|u_{1}\right| \geqslant z_{\alpha / 4} \quad\) 或 \(\quad\left|u_{2}\right| \geqslant z_{\alpha / 4}\)

下面来验证当 \(n\) 充分大时上述检验法近似地满足显著性水平为 \(\alpha\) 的要求. 事实上当 \(n\) 充分大时有： \(P\left\{\right.\) 当 \(H_{0}\) 为真拒绝 \(\left.H_{0}\right\}\) \(=P_{H_{0}}\left\{\left(\left|U_{1}\right| \geqslant z_{\alpha / 4}\right) \cup\left(\left|U_{2}\right| \geqslant z_{\alpha / 4}\right)\right\}\) \(\leqslant P_{H_{0}}\left\{\left|U_{1}\right| \geqslant z_{\alpha / 4}\right\}+P_{H_{0}}\left\{\left|U_{2}\right| \geqslant z_{\alpha / 4}\right\}=\frac{\alpha}{2}+\frac{\alpha}{2}=\alpha\)

秩和检验

//TODO 秩和检验

假设检验问题的 \(p\) 值检验法

以上讨论的假设检验方法称为临界值法. 本节介绍另一种被称为 \(p\) 值检验法的检验方法. 先从一个例题讲起.

例子： 设总体 \(X \sim N\left(\mu, \sigma^{2}\right), \mu\) 未知 \(, \sigma^{2}=100,\) 现有样本 \(x_{1}, x_{2}, \cdots, x_{52},\) 算得\(\bar{x}=62.75 .\) 现在来检验假设\(H_{0}: \mu=\mu_{0}=60, \quad H_{1}: \mu>60\)

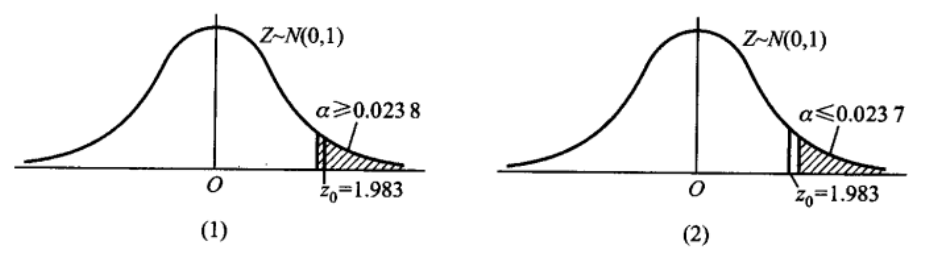
采用 \(Z\) 检验法,检验统计量为\(Z=\frac{\bar{X}-\mu_{0}}{\sigma / \sqrt{n}}\) 以数据代人,得 \(Z\) 的观察值为\(z_{0}=\frac{62.75-60}{10 / \sqrt{52}}=1.983\)

概率\(P\left\{Z \geqslant z_{0}\right\}=P\{Z \geqslant 1.983\}=1-\Phi(1.983)=0.0238\) 此即为标准正态曲线下-位于 \(z_{0}\) 右边的尾部面积.

此概率称为 \(Z\) 检验法的右边检验的 \(p\) 值. 记为\(P\left\{Z \geqslant z_{0}\right\}=p\) 值 \((这里=0.0237)\)

若显著性水平 \(\alpha \geqslant p=0.0238\),（如上图（1）），则对应的临界值 \(z_{\alpha} \leqslant 1.983\), 这表示观察值 \(z_{0}=1.983\) 落在拒绝域内，因而拒绝 \(H_{0}\); 又若显著性水平 \(\alpha<p=\) 0.0238 ,（如上图（2）），则对应的临界值 \(z_{\alpha}>1.983\), 这表示观察值 \(z_{0}=1.983\) 不落在拒绝域内 ， 因而接受 \(H_{0}\). 据此 \(, p\) 值 \(=P\left\{Z \geqslant z_{0}\right\}=0.0238\) 是原假设 \(H_{0}\) 可被拒绝的最小显著性水平。

一般, \(p\) 值的定义是 : 定义：假设检验问题的 \(p\) 值（probability value )是由检验统计量的样本观察值得出的原假设可被拒绝的最小显著性水平.

任一检验问题的 \(p\) 值可以根据检验统计量的样本观察值以及检验统计量 在 \(H_{0}\) 下一个特定的参数值(一般是 \(H_{0}\) 与 \(H_{1}\) 所规定的参数的分界点)对应的分布求出. 例如在正态总体 \(N\left(\mu, \sigma^{2}\right)\) 均值的检验中,当 \(\sigma\) 未知时,可采用检验统计量 \(t=\frac{\bar{X}-\mu_{0}}{S / \sqrt{n}},\) 在以下三个检验问题中,当 \(\mu=\mu_{0}\) 时 \(t \sim t(n-1) .\) 如果由样本求得统计量 \(t\) 的观察值为 \(t_{0}\),那么在检验问题 \(H_{0}: \mu \leqslant \mu_{0}, H_{1}: \mu>\mu_{0}\) 中, \(p\) 值 \(=P_{\mu_{0}}\left\{t \geqslant t_{0}\right\}=t_{0}\) 右侧尾部面积; \(H_{0}: \mu \geqslant \mu_{0}, H_{1}: \mu<\mu_{0}\) 中, \(p\) 值 \(=P_{\mu_{0}}\left\{t \leqslant t_{0}\right\}=t_{0}\) 左侧尾部面积; 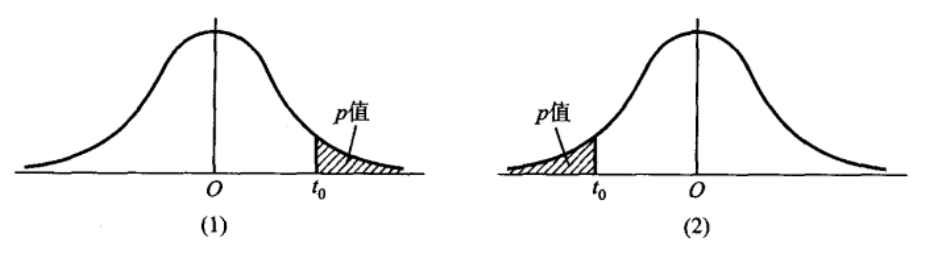\(H_{0}: \mu=\mu_{0}, H_{1}: \mu \neq \mu_{0}\) 中, (i) 当 \(t_{0}>0\) 时, \(p \text { 值 }=P_{\mu_{0}}\left\{|t| \geqslant t_{0}\right\}=P_{\mu_{0}}\left\{\left(t \leqslant-t_{0}\right) \cup\left(t \geqslant t_{0}\right)\right\}\)\(=2 \times\left(t_{0}\right.\) 右侧尾部面积) (ii) 当 \(t_{0}<0\) 时, \(p \text { 值 }=P_{\mu_{0}}\left\{|t| \geqslant-t_{0}\right\}=P_{\mu_{0}}\left\{\left(t \leqslant t_{0}\right) \cup\left(t \geqslant-t_{0}\right)\right\}\)\(=2 \times\left(t_{0}\right.\) 左侧尾部面积 \()\) 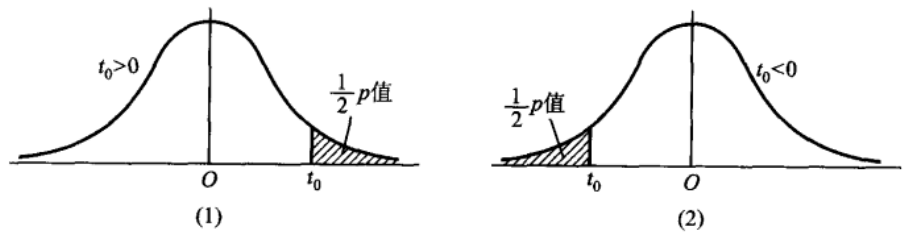上述各图中的曲线均为 \(t(n-1)\) 分布的概率密度曲线.

在现代计算机统计软件中,一般都给出检验问题的 \(p\) 值. 按 \(p\) 值的定义,对于任意指定的显著性水平 \(\alpha\),就有 (1) 若 \(p\) 值 \(\leqslant \alpha\),则在显著性水平 \(\alpha\) 下拒绝 \(H_{0}\). (2) 若 \(p\) 值 \(>\alpha\),则在显著性水平 \(\alpha\) 下接受 \(H_{0}\).

有了这两条结论就能方便地确定 \(H_{0}\) 的拒绝域. 这种利用 \(p\) 值来确定检验 拒绝域的方法,称为 \(p\) 值检验法.

用临界值法来确定 \(H_{0}\) 的拒绝域时,例如当取 \(\alpha=0.05\) 时知道要拒绝 \(H_{0}\), 再取 \(\alpha=0.01\) 也要拒绝 \(H_{0}\),但不能知道将 \(\alpha\) 再降低一些是否也要拒绝 \(H_{0} .\) 而 \(p\) 值法给出了拒绝 \(H_{0}\) 的最小显著性水平. 因此 \(p\) 值法比临界值法给出了有关拒绝域的更多的信息.

\(p\) 值表示反对原假设 \(H_{0}\) 的依据的强度, \(p\) 值越小,反对 \(H_{0}\) 的依据越强、越 充分 (端如对于某个检验问题的检验统计量的观察值的 \(p\) 值 \(=0.0009, p\) 值如 此的小,以至于几乎不可能在 \(H_{0}\) 为真时出现目前的观察值,这说明拒绝 \(H_{0}\) 的 理由很强,我们就拒绝 \(H_{0}\) ).

一般,若 \(p\) 值\(\leqslant 0.01\),称推断拒绝 \(H_{0}\) 的依据很强或称检验是高度显著的; 若 \(0.01<p\) 值 \(\leqslant 0.05\) ,称推断拒绝 \(H_{0}\) 的依据是强的或称检验是显著的; 若 0.05 \(<p\) 值\(\leqslant 0.1\) ,称推断拒绝 \(H_{0}\) 的理由是弱的,检验是不显著的; 若 \(p\) 值 \(>0.1\) 一 般来说没有理由拒绝 \(H_{0} .\) 基于 \(p\) 值,研究者可以使用任意希望的显著性水平来作计算。在杂志上或在一些技术报告中，许多研究者在讲述假设检验的结果时，常不明显地论及显著性水平以及临界值，代之以简单地引用假设检验的p值，利用或让读者利用它来评价反对原假设的依据的强度，作出推断.