线性代数-相似矩阵与二次型习题

线性代数-相似矩阵与二次型习题

内积,正交的概念

内积的概念

例1
image-20201012145035553
image-20201012145106438

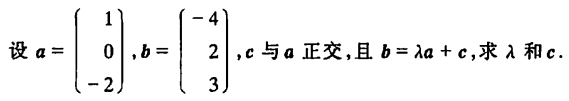
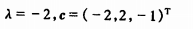
正交矩阵的判定与证明

可用正交矩阵的定义\(A^T A = E\)判断, 也可用\(A^T=A^{-1}\)判断, 也可用构成A向量组的向量是否都两两正交,且向量都是单位向量来判断

例1
image-20201012151808714
image-20201012151832177
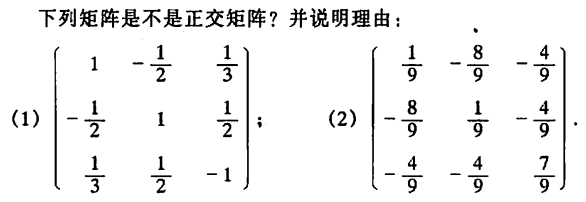
例2
image-20201012153113164

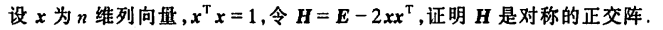
略

例3
image-20201012161359690

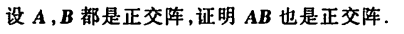
证明： A、B是正交矩阵，根据定义知道AA’=A’A=E, BB’=B’B=E, 那么(AB)(AB)‘=(AB)(B’A’)=ABB’A’=A(BB’)A=AEA’=AA’=E

线性无关向量组的正交化(施密特正交化)

例1
image-20201012150738793
image-20201012150855741

特征值与特征向量

求特征值与特征向量

例1
image-20201013105735880
image-20201013105806041

特征值的证明

特征值相同的证明

一般根据\(Ax=\lambda x, x\neq 0\)的定义,化为齐次方程组\((A-\lambda E)x = 0, x\neq 0\), 利用齐次方程组有非零解的条件求特征值, 即用\(|A-\lambda E|=0\)来证明特征值相等.

也有习题是从\(Ax=\lambda x, x\neq 0\)的定义,直接入手,用矩阵乘法等来做.

例1
image-20201013110513743
例2
image-20201018023250370

image-20201018023455602 参考:https://blog.csdn.net/qq_37430422/article/details/106255194

特征值是给定值的证明

方法一:直接求 方法二:用特征值的性质求

例1
image-20201014113240513

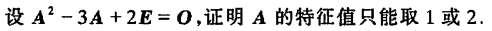
方法一:

img

方法二: 首先，（A-2E）（A-E）=0。也就是说A-E的每一列都在A-2E的解空间之内，所以R(A-2E)+R(A-E)<=n。 （这个也可以直接由Sylvester不等式得到。对于任意两个n阶矩阵A和B，必有r(A)+r(B)<=r(AB)+n） 假如R(A-2E)+R(A-E)<n，那就是说A-2E的解空间和A-E的解空间必定有非零交集。也就是说存在列向量x使得（A-2E）x=0且（A-E）x=0，两式相减，就发现Ex=0，所以x只能等于0，矛盾。 所以只能有R(A-2E)+R(A-E)=n

例2
image-20201014114439288

方法一: 当\(\lambda=-1\)时, \(|A-\lambda E| = |A+E|\), 又A正交(即\(AA^T=E\), \(|A|=-1\)), 则\(|A+E|=|A+AA^T| = |A(E+A^T)| = |A|\cdot |E+A^T| = - |E+A|\) 即\(|A+E|=-|A+E|\) 则\(|A+E|=0\) 即当\(\lambda=-1\)是A的特征值

方法二: 符号||既能代表向量（n×1阶）的模，又能代表方阵（n×n阶）的行列式，两个概念不能混淆。 |x|代表向量的模，一般不能直接与|A|这个行列式值相乘得到Ax的模。常数k的话，倒是可以相乘的，即kx的模等于k的模乘向量x的模。 正交矩阵的性质是Ax的模和x的模相等，即|Ax|=|x|（这是因为|Ax|2=(Ax)‘(Ax)=x’A’Ax=x’(A’A)x=x’Ix=x’x=|x|2）。由Ax=lamdax，两边取模|x|=|lamda||x|，因为|x|非零，因此可以推出|lamda|=1，即正交矩阵的特征值的模是1（包括复数的模）。 这道题的一个正确做法是：A的特征多项式的根即A的特征值，前面已经证明了他们的模都是1，而且复数特征值都是成对共轭地出现（代数基本定理，实系数多项式的复数根都是共轭成对出现），因为行列式等于特征值的乘积，所以 lamda(1)lamda(2)…*lamda(n)=|A|=-1， 如果lamda里没有-1，那个A的实特征值只能有+1，而且共轭模1的特征值的成对乘积都是+1，所以|A|就应该是+1，而不是-1，这就矛盾了。 https://zhidao.baidu.com/question/513861568.html

例3 !!!!
image-20201019183352818
image-20201019190938858

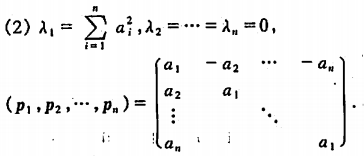
a=(a1,a2,…,an)T,a1≠0，A=aaT, 所以R(A)<=R(a)<=1 又a1≠0，所以R(A)=1 故A有n-1重0特征值，其非零特征值为a12+a22+…+an^2 https://zhidao.baidu.com/question/496459585060051324.html?&mzl=qb_xg_0&word=

注: R(AB)<=R(A) \(\lambda_1+\lambda_2+...+\lambda_n = a_{11}+a_{22}+...+a_{nn}\)

有一个特征值是a12+a2+…+an^2.他的特征向量怎么求: Aα =ααTα = α(αTα) = α(a12+a2+…+an^2) = (a12+a2+…+an^2)α

注意到 \(a a^T x=0\) 与 \(ax=0\) 同解

所以属于特征值0的特征向量即与向量a正交的非零向量. 不妨设a1≠0, 则ax=0的基础解系为 (-a2/a1, 1,0,0,…,0)^T, (-a3/a1,0,1,…,0)^T, … , (-an/a1,0,0,…,1)^T \(A=a a^T\)的属于特征值0的特征向量即为上述基础解系的非零线性组合 https://zhidao.baidu.com/question/543883728.html

有相同特征向量的证明

实际上就是齐次方程组的公共解问题

例1
image-20201013113109156
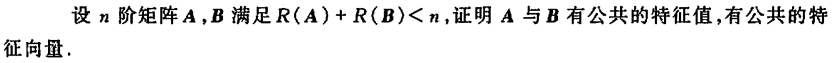
  1. rank(A)<=rank(A)+rank(B)<n，所以A不是满秩的，所以存在x≠0使得Ax=0，即0是A的一个特征值。同理可证0也是B的一个特征值。所以A与B有公共的特征值0。
  2. 只需证明存在x≠0使得Ax=0且Bx=0，则x同时是A与B对应于特征值0的特征向量。 方法一：Ker(A)={x≠0|Ax=0}和Ker(B)={x≠0|Bx=0}都是Rn的线性子空间，且dimKer(A)=n-rank(A),dimKer(B)=n-rank(B)，所以dimKer(A)+dimKer(B)=2n-(rank(A)+rank(B))>2n-n=n=dimRn。所以dim(Ker(A)∩Ker(B))>=dimKer(A)+dimKer(B)-dimR^n>0。再任取Ker(A)∩Ker(B)中的非零元x即可。 方法二：Ax=0且Bx=0当且仅当(A|B)x=0，其中(A|B)为A和B拼成的矩阵。注意到A的列向量空间中的一组基和B的列向量空间中的一组基的并可以组成(A|B)的列向量空间中的一组生成元（未必是基），所以(A|B)的列秩不大于A和B的列秩的和。从而rank(A|B)<=rank(A)+rank(B)<n，得dimKer(A|B)=n-rank(A|B)>0。再任取Ker(A|B)中的非零元x即可。
img

参考:https://zhidao.baidu.com/question/149727470.html

矩阵相似

证明矩阵相似

例1
image-20201018032601047

证明: 因为A可逆, 则有\(A^{-1} AB A = BA\) 即AB与BA相似.

矩阵相似对角化

矩阵可相似对角化的判断

例1
image-20201019121208151
image-20201019121221653

解: (1)用\(Ap = \lambda p\)来求a,b,\(\lambda\) (2)A是3阶方阵,需要判断是否有3个线性无关的特征向量. 先\(|A-\lambda E| = 0\)求特征值,然后求每个特征值对应的解向量,判断每个解空间的秩是否等于特征值的重数.

利用相似对角化求矩阵的幂,多项式及其行列式

例1
image-20201018030139496

解: 3阶矩阵A有三个不同的特征值,则A有3个互相线性无关的特征向量,则A的秩为3,A可逆. \(|A^3-5A^2+7A|\\=|P^{-1} (\Lambda^3-5\Lambda^2+7\Lambda) P|\\=|P^{-1}|\cdot |(\Lambda^3-5\Lambda^2+7\Lambda)|\cdot |P|\\=|(\Lambda^3-5\Lambda^2+7\Lambda)|=18\)

例2
image-20201018031651293

答案:25

例3
image-20201019134757419
image-20201019134809739

解:求特征值,特征向量,拼成\(\Lambda\)对角阵和\(P^{-1}A P = \Lambda\)中的P矩阵

例4
image-20201019144145816

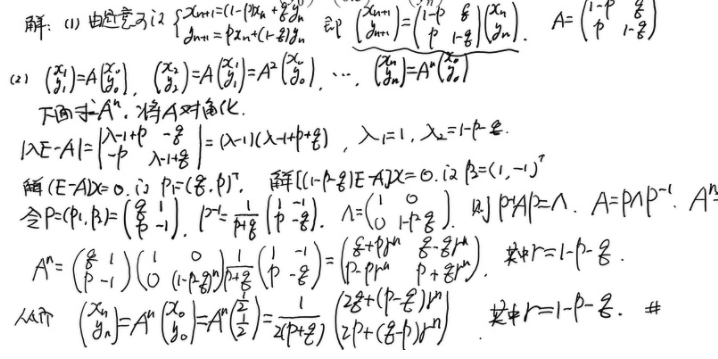image-20201019144201944 参考:http://www.math110.com/Teaching/MathHome/ExerciseShow?guid=BC2310EA-B16A-4AE6-B196-E21B5BBFE24A&&cguid=20F57A7D-31E7-4B96-B292-922F189144FE&&cname=%E7%BA%BF%E6%80%A7%E4%BB%A3%E6%95%B0

例5
image-20201019183706785
image-20201019183746271

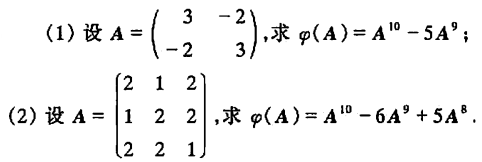
根据特征值与特征向量求矩阵

根据特征值与特征向量求一般矩阵
例1
image-20201019160305450
image-20201019160316025
image-20201019160328944

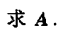
解:根据矩阵可相似对角化的充要条件:有n个现象无关的特征向量,可知A一定可相似对角化 \(P^{-1}AP = \Lambda\),则\(A= P \Lambda P^{-1}\)

根据特征值与特征向量求对称矩阵
例1
image-20201019162958112
image-20201019160316025
image-20201019163022790
解:根据对称矩阵的性质:对称阵A特征值\(\lambda_1 \neq \lambda_2\)\(\Rightarrow\)特征向量\(p_1,p_2\)正交 设\(\lambda_3\)对应的特征向量为\(p_3 = (x_1,x_2,x_3)^T\),则\(p_1^T p_3 = 0, p_2^T p_3=0\) 则有\(\left(\begin{array}{cc}p_1 \\ p_2\end{array}\right) p_3 = O\) 即$( \[\begin{array}{ccc}1 & 2 & 2 \\ 2 & 1 & -2\end{array}\] )( \[\begin{array}{cc}x_1 \\ x_2\\ x_3\end{array}\] ) = ( \[\begin{array}{cc}0 \\ 0\end{array}\]

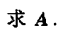
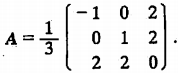
) $ 解此方程组,得通解 \(x=k\left(\begin{array}{cc}2 \\ -2\\ -1\end{array}\right)\),要作为特征向量时,\(k \neq 0\) 可取\(p_3 = \left(\begin{array}{cc}2 \\ -2\\ -1\end{array}\right)\)

接下来:

对称矩阵一定可以相似对角化

\(P^{-1}AP = \Lambda\),则\(A= P \Lambda P^{-1}\)

…

例2
image-20201019174356855
image-20201019174406107

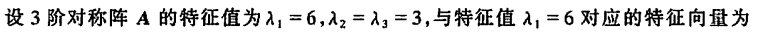
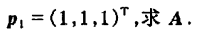
image-20201019174431648 https://zhidao.baidu.com/question/2075815010174660988.html?qbl=relate_question_1 https://zhidao.baidu.com/question/2272849277510279468.html?qbl=relate_question_0 https://zhidao.baidu.com/question/2075815010174660988.html

根据可相似对角化求矩阵参数

例1
image-20201018181209472

n阶方阵A可对角化等价于方阵有n个线性无关的特征向量，由于不同特征值对应的特征向量必然不相关，故只需要其特征值的k重根有k个线性无关的特征向量。 A的特征值分别为1,1,6，故 R(E - A) = 1，带入可知 x = 3

例2
image-20201019154724021

对称矩阵相似对角化/正交化

先求特征值,特征向量,用作出与矩阵相似的对角矩阵\(\Lambda\), 对各特征向量施密特正交化,然后用正交的特征向量拼成对应的可逆矩阵Q,则\(Q^{-1} A Q = \Lambda\)

例1
image-20201019151545448
image-20201019154818931
例2
image-20201019154724021

二次型及其矩阵

二次型的矩阵

例1
image-20201020110244825
image-20201020110312617
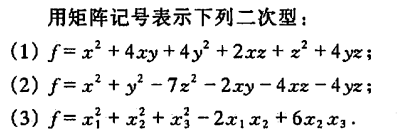
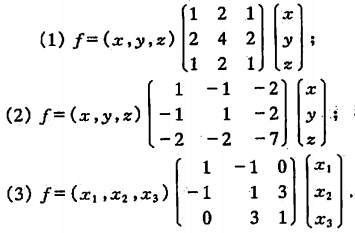
例2
image-20201020110345941
image-20201020110400927

二次型化为标准型或规范型

正交变换法化为标准型或规范型

例1
image-20201020112736516
image-20201020112752438
image-20201020112807180
例2
image-20201020113338112
image-20201020113351116
image-20201020113537971

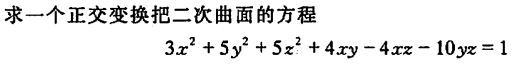
用配方法化为标准型或规范型

例1
image-20201020193837408
image-20201020193846165
image-20201020193857267
image-20201020193911644

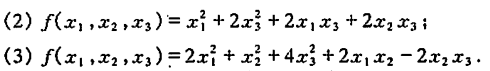
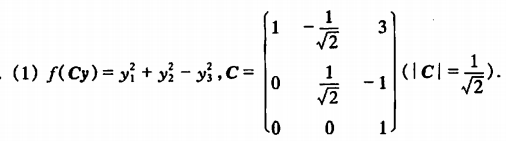
二次型的最大值

例1
image-20201020164357986

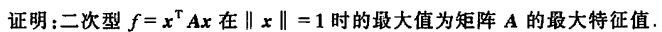
证明:

二次型\(f=x^T A x\)的矩阵A是对称阵,必可正交对角化: \(C^T A C=C^{-1}A C = \left(\begin{array}{cccc}\lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots & \\ & & & \lambda_{n}\end{array}\right)=\Lambda\),其中\(|C| \neq 0\),且C是正交阵 即二次型\(f=x^T A x= y^T \Lambda y\)对应的变换为\(x=Cy\) 又根据\(\|x\|=1\),有\(\|\boldsymbol{x}\|=\sqrt{\boldsymbol{x}^{\mathrm{T}} \boldsymbol{x}}=\sqrt{\boldsymbol{y}^{\mathrm{T}} \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C x}}=\sqrt{\boldsymbol{y}^{\mathrm{T}} \boldsymbol{y}}=\|\boldsymbol{y}\|=1\), 即\(\sqrt{y_{1}^{2}+y_{2}^{2}+\cdots+y_{n}^{2}}=1\),即\(y_{1}^{2}+y_{2}^{2}+\cdots+y_{n}^{2}=1\). 不妨设\(\Lambda\)中最大的特征值为\(\lambda_1\) 则$f=y^T y=({1} y{1}{2}++{n} y{n}{2}) $ \(\leqslant \lambda_1(y_{1}^{2}+y_{2}^{2}+\cdots+y_{n}^{2})=\lambda_1\)

正定二次型

已知正定求参数范围

正定二次型的矩阵,各阶主子式全为正, 负定二次型的矩阵,奇数阶主子式全为负,偶数阶主子式全为正

例1
image-20201020200925531
image-20201020200934070
image-20201020201003327

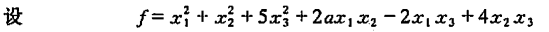
判定二次型是否正定或负定

二次型正定,是指二次型的结果必大于0,

实际上,一般利用二次型正定的充分必要条件:特征值全为正.来判断 这就化为标准型,根据标准型来看

例1
image-20201020201219788
image-20201020201535522

二次型充要条件的证明

例1
image-20201020201958651

可参考如下定理的证明: \(n\) 元二次型 \(f=x^{\mathrm{T}} A x\) 为正定的\(\Leftrightarrow\)它的标准型的n个系数全为正\(\Leftrightarrow\)它的规范型的n个系数都为1\(\Leftrightarrow\)它的正惯性系数等于n

证明 设存在可逆变换\(x=C y\) 使\(f(x)=f(C y)=\sum_{i=1}^{n} k_{i} y_{i}^{2}\)

充分性: 设 \(k_{i}>0(i=1, \cdots, n) .\) 任给 \(x \neq 0,\) 则 \(y=C^{-1} x \neq 0,\) 故\(f(x)=\sum_{i=1}^{n} k_{i} y_{i}^{2}>0\)

必要性: 用反证法. 假设$ k_s $, 则当 \(y = e_s\) (单位坐标向置)时, \(f(x)=f(Cy)=f\left(C e_{s}\right)=k_{t} \leqslant 0\) 这与二次型正定矛盾.故\(k_s>0\) 则\(k_1,\cdots,k_n\)都可用反证法证明大于0