线性代数-矩阵1习题

矩阵的基本运算

主要涉及矩阵加法、数乘、乘法、转置。

矩阵的乘法

矩阵乘法的计算

例1

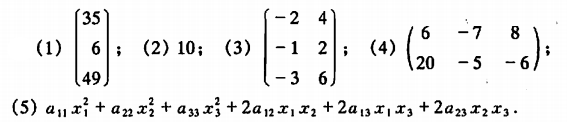
例2

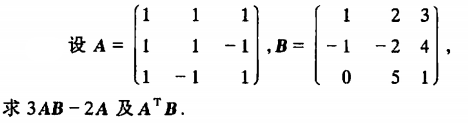
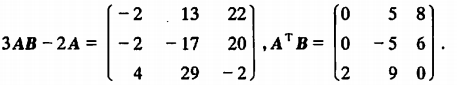
例3

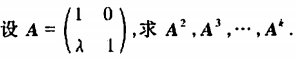
例4 这题没做出来

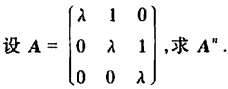
例5

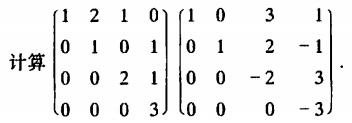
矩阵乘法的性质

例1 一般矩阵乘法不可交换

例2 基本消元不成立

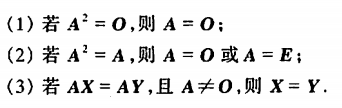
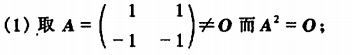
求逆矩阵

直接求逆矩阵

二阶：逆矩阵为：行列式分之伴随

高阶：\((A|E) \rightarrow (E | A^-1)\)

例1

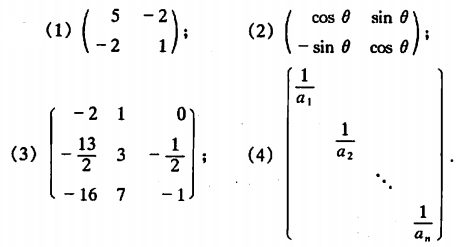
例2

例3

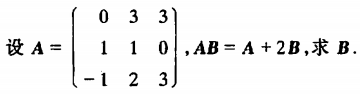
例4

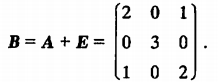
例5

例6

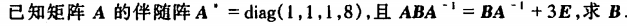
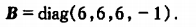
解矩阵方程

线性变换可以表示为矩阵方程。线性变化与矩阵方程一一对应。

例1

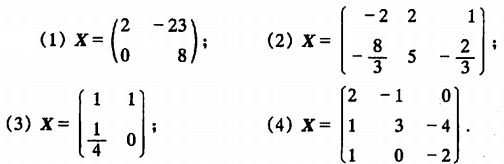
例2

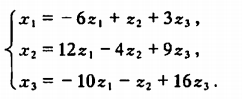
例3

例4

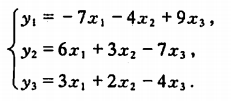
可对角化矩阵多项式求解

例1

例2

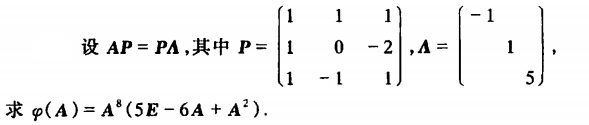
分块矩阵

例1

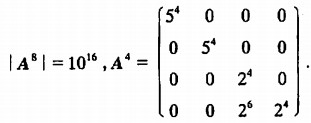
例2 不会证

\(\left(\begin{array}{ll}O & A \\ B & O\end{array}\right)^{-1} = \left(\begin{array}{cc} O & B^{-1} \\ A^{-1} & O \end{array}\right)\)

\(\left(\begin{array}{ll}A & O \\ C & B\end{array}\right)^{-1} = \left(\begin{array}{cc} A^{-1} & 0 \\ -B^{-1} C A^{-1} & B^{-1} \end{array}\right)\)

例3

矩阵的证明

证明矩阵是对称矩阵

例1

\(\boldsymbol{B}^{T} \boldsymbol{A} \boldsymbol{B} = ((AB)^T B)^T = (B^T A^T B)^T\) 又A是对称阵，即\(A^T = A\) 则$(B^T A^T B)^T = (B^T A B)^T $

所以$^{T} = (B^T A B)^T \(，即\)B^T A B$是对称阵。

例2

注：写出元素，用定义证明。

逆矩阵的证明

例1

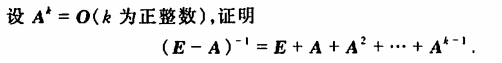
证明:因为 A^k = 0 所以 (E-A)(E+A+A^2+…+A(k-1)) = E+A+A^2+…+A(k-1) -A-A^2-…-A(k-1)-A^k = E - A^k = E 所以 E-A 可逆,且 (E-A)^-1 = E+A+A^2+…+A(k-1)

例2

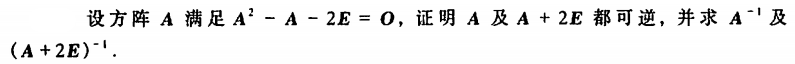
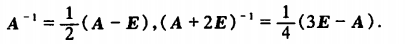
例3

AA＝|A|E，AA^-1＝E .所以A＝|A|A^-1.既A*可逆。接下来就好做了。。。

伴随矩阵的证明

例1

（1）证明: 假设\(|a^*|≠0\) 由\(a^*\)可逆 因为\(aa^*=|a|a=0\) 等式两边右乘\((a^*)^-1\)则得 \(a=0\) 故\(a^*=0\) 所以\(|a^*|=0\) 与假设矛盾.

（2）略