线性代数-矩阵初等变换与线性方程组习题
线性代数-矩阵初等变换与线性方程组习题
矩阵初等变换
变换成最简型
例1


求初等变换矩阵
初等行变换\(A \rightarrow E\) 即\(PA = E\) 又\(PE = P\) 则\((P|E) \rightarrow (E|P)\)
例1


例2 A不是方阵时,可逆矩阵可能不唯一


我用初等行变换的方法做第二问,得到的答案是: \(Q=\left(\begin{array}{rrr}1 & 2 & 0 \\ -1 & -2 & 1 \\ -4 & -7 & 1\end{array}\right)\) 与标准答案不同。 参考网上的意思是:当\(A^T\)(或\(A\))不是方阵时,Q不唯一。 https://zhidao.baidu.com/question/1695810374576283988.html?qbl=relate_question_4 https://m.iask.sina.com.cn/b/20287408.html
求逆矩阵
例1


例2


例3


矩阵的秩
初等变换前后的矩阵是同型矩阵。
初等变换不改变矩阵的秩,即同型矩阵的秩相等。
秩的概念与证明
例1


例2


例3 用到后面向量的线性无关概念


找线性无关的向量: https://zhidao.baidu.com/question/265408643.html
例4 证明等价矩阵的秩相等

1)先证明:若 A 经一次初等行变换变为 B,则 \(R(A) \leqslant R(B)\) 设 \(R(\boldsymbol{A})=r,\) 且 \(\boldsymbol{A}\) 的某个 \(r\) 阶子式 \(D \neq 0\)。设进行一次初等行变换后,与 D 相对应的 r 阶子式为 \(D_1\). 1.1)当对A进行的是行置换或倍乘变换时,\(D_{1}=\pm D\) 或 \(D_{1}=k D,\) 因此 \(D_{1} \neq 0,\) 从而 \(R(\boldsymbol{B}) \geqslant r\) 1.2)当对A进行的是行倍加变换时,可假设是在第一行与第二行进行倍加(其他行的情形可通过行置换变到第一二行)。需要分为两种情况来讨论: 1.2.1)若A 的 r 阶非零子式 D 不包含 A 的第 1 行,这时 D 也是 B 的 r 阶非零子式,故 \(R(B) \geqslant r\); 1.2.2)若\(D\) 包含 A 的第 1 行,这时把 B 中与 D 对应的 r 阶子式 \(D_1\), 记作\(D_{1}=\left|\begin{array}{c}r_{1}+k r_{2} \\ r_{p} \\ \vdots \\ r_{q}\end{array}\right|=\left|\begin{array}{c}r_{1} \\ r_{p} \\ \vdots \\ r_{q}\end{array}\right|+k\left|\begin{array}{c}r_{2} \\ r_{p} \\ \vdots \\ r_{q}\end{array}\right|=D+k D_{2}\) 若 \(p=2,\) 则 \(D_{1}=D \neq 0 ;\) 若 \(p \neq 2,\) 则 \(D_{2}\) 也是 \(\mathbf{B}\) 的 \(r\) 阶子式。由 \(D_{1}-k D_{2}=D \neq 0,\) 知 \(D_{1}\) 与\(D_{2}\)不同时为0.总之, B 中存在 \(r\) 阶非零子式 \(D_{1}\) 或 \(D_{2},\) 故 \(R(\boldsymbol{B}) \geqslant r\)
以上证明了若 A 经一次初等行变换变为 B,则 \(R(A) \leqslant R(B)\)
2)由于B也可通过一次行变换变为 A ,故也有 \(R(\boldsymbol{B}) \leqslant R(\boldsymbol{A}) .\) 因此经过一次初等行变换从A变换到B,有 \(R(\boldsymbol{A})=R(\boldsymbol{B})\)
3)经过有限次初等行变换从A变换到B,有 \(R(\boldsymbol{A})=R(\boldsymbol{B})\)
4)设 A 经 初 等 列 变 换 变 为 B,则 \(A^T\) 经 初 等 行 变 换 变 为 \(\mathbf{B}^{\mathrm{T}}\), 由 上 段 证 明 知 \(R\left(A^{\top}\right)=R\left(B^{\top}\right),\) 又 \(R(A)=R\left(A^{\top}\right), R(B)=R\left(B^{\top}\right),\) 因此 \(R(A)=R(B)\)
例5
证明r(A)=1的充分必要条件是存在非零列向量a及非零行向量\(b^T\),使\(A=ab^T\)
证: 必要性. 因为bai R(A)=1 所以 A有一个非零行du, 且其余行都是此行的倍数 设此行为zhi b^T 则 A = k1b^T … b^T knb^T 令 a = (k1,…,1,…,kn)^T 则 A=ab^T 充分性dao. 因为存在非零列向量a及非零行向量bT,使A=abT 所以A≠0. 所以 R(A)>=1. 又 R(A)=R(ab^T)<=R(a)=1 所以 R(A)=1. https://zhidao.baidu.com/question/299102973.html
例6
设A为列满秩矩阵,AB=C,证明Bx=0与Cx=0同解
首先, 若X是baiBX = 0的解du, 则CX = ABX = 0, 即X也是CX = 0的解. 反之, 若X是CX = 0的解, 有ABX = CX = 0, 即Y = BX是AY = 0的解. 而由A列满秩, AY = 0只有零zhi解, 故BX = Y = 0, 即X也是BX = 0的解. 综合两dao方面, BX = 0与CX = 0同解. 还有一种方法: 由A列满秩可得r(B) ≥ r(AB) ≥ r(A)+r(B)-n = r(B) (n表示A的列数), 故r(C) = r(AB) = r(B). 因此BX = 0与CX = 0解空间维数相等. 又易见前者的解空间包含于后者, 因此二者解空间相同. https://zhidao.baidu.com/question/304276864816318884.html
例7
设A为m×n矩阵,证明方程AX=Em有解的充分必要条件为r(A)=m
充分性:当r(A)=m时,bai则A是行满秩的,A多添任一列向du量组成的zhi增光矩阵还是行满秩的,即有r(A ei)=m,其中daoei是单位阵的第i列,于是方程Ax=ei有解bi,令X=【b1 b2 … bm】,则AX=E。 必要性:若AX=E有解,则m=r(Em)=r(AX)<=r(A)<=m,于是r(A)=m https://zhidao.baidu.com/question/371476936.html
求矩阵的秩
直接计算矩阵的秩
初等变换变为标准型可以求矩阵的秩
例1


讨论矩阵的秩
矩阵中有参数存在,矩阵的秩需要讨论。
例1


解线性方程组
解齐次线性方程组
例1

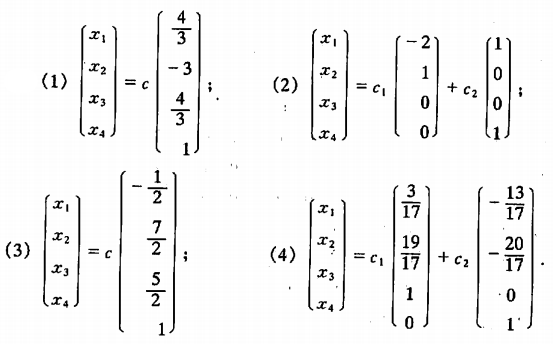
例2


解非齐次线性方程组
例1



方程组解的讨论
其实还是解线性方程组的流程,只是需要讨论参数。
例1

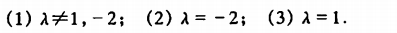
例2


(注意:这里很容易漏掉其中一种情况)
例3

