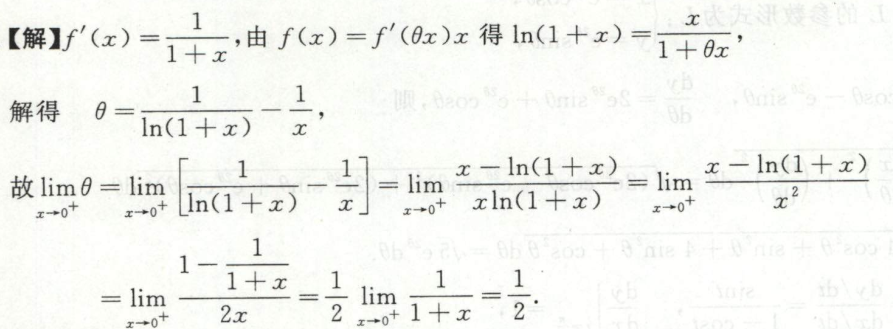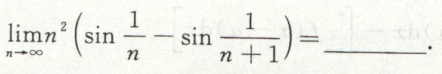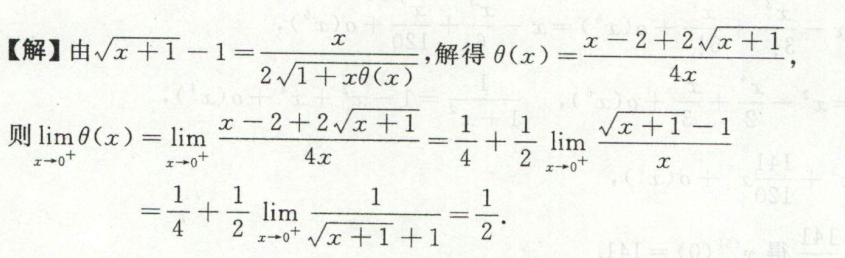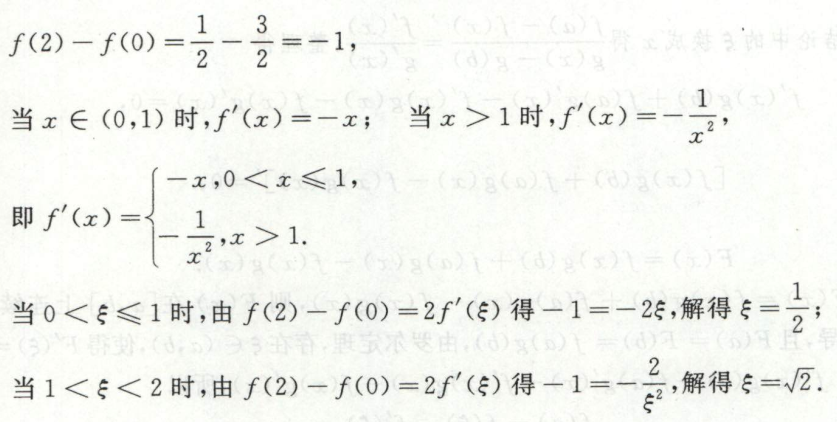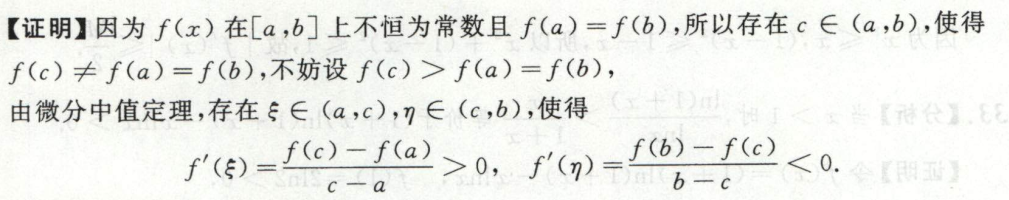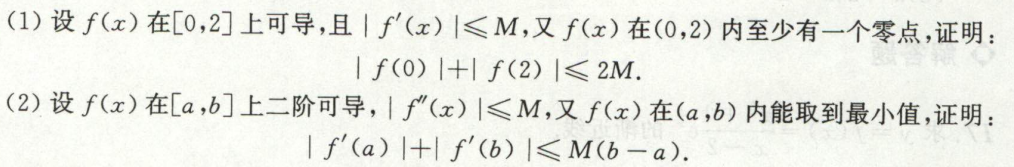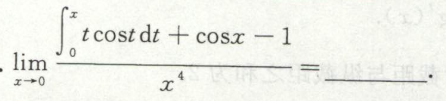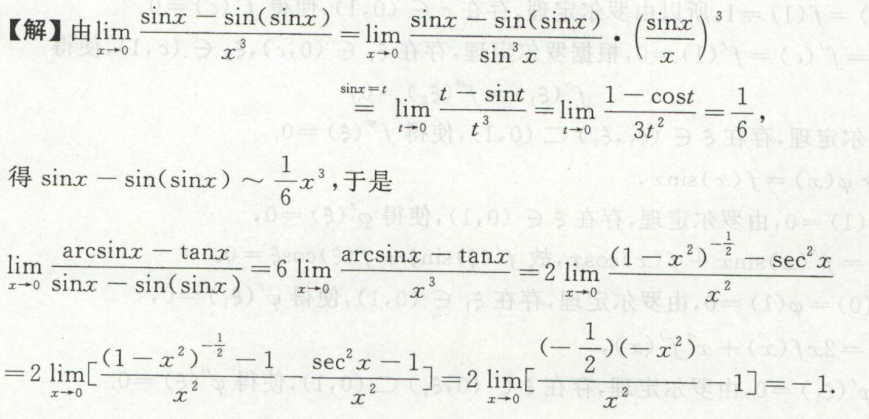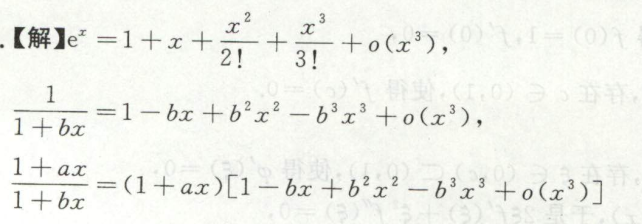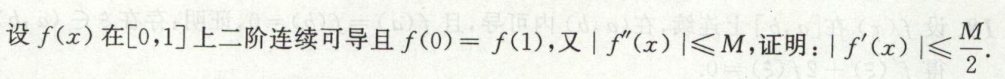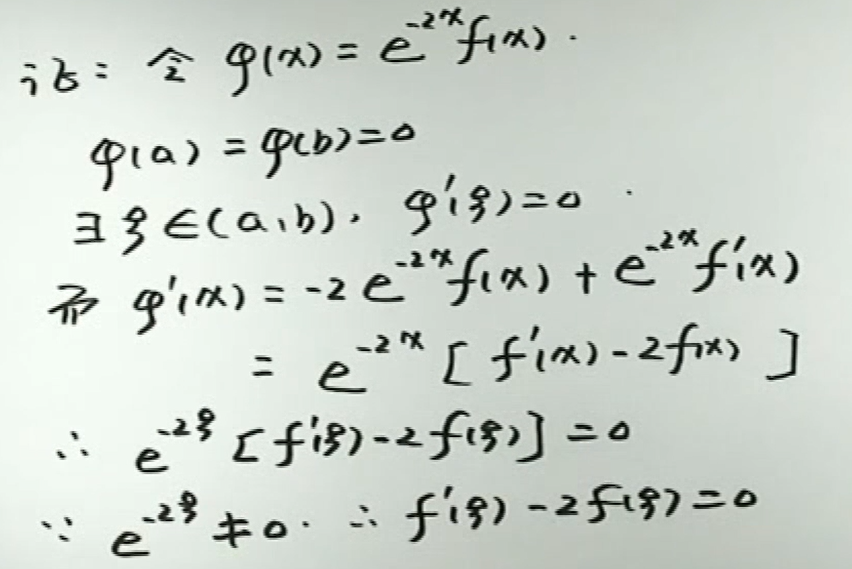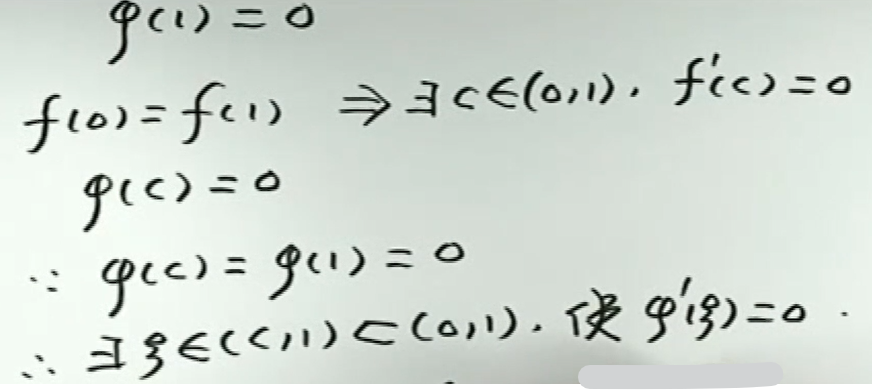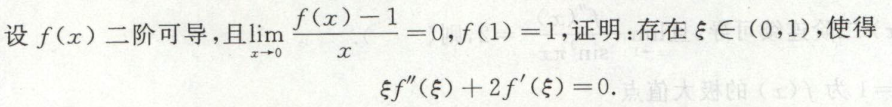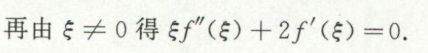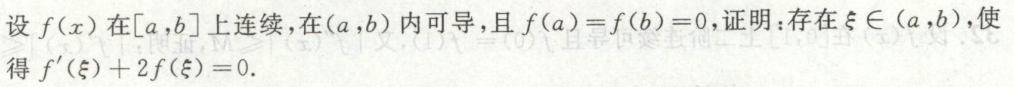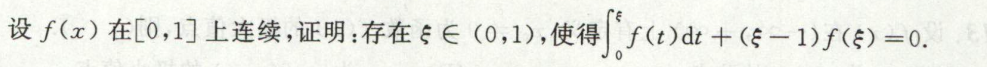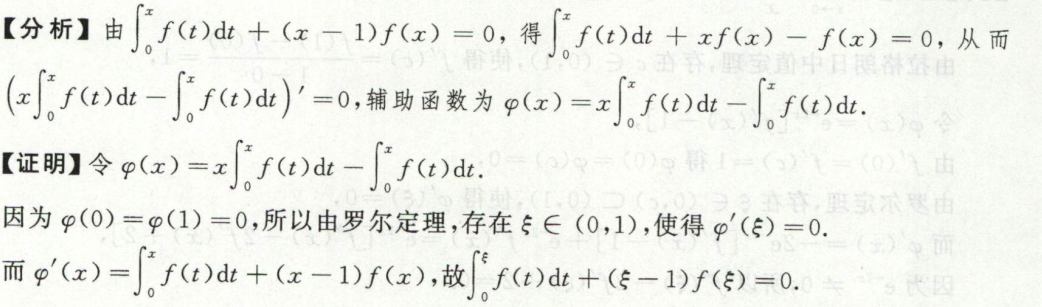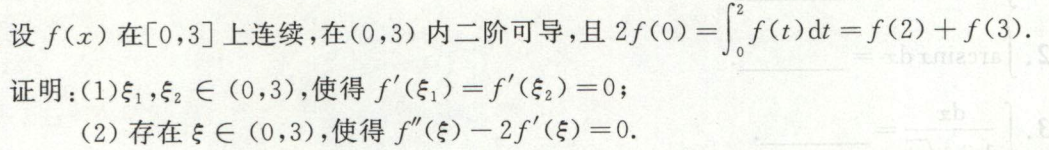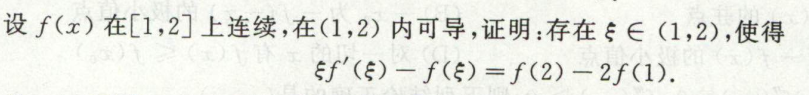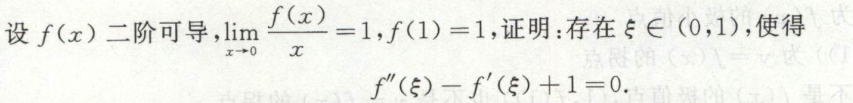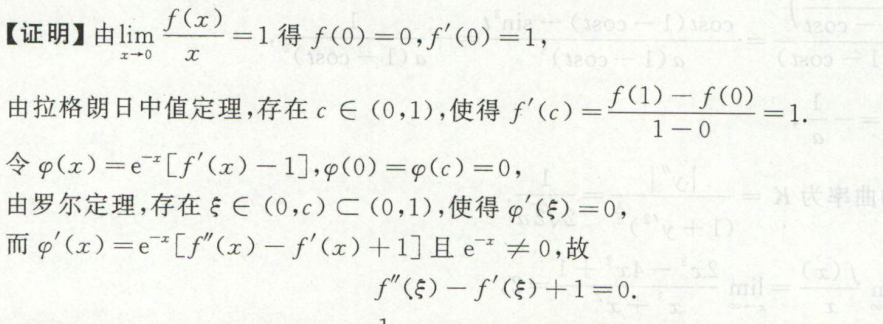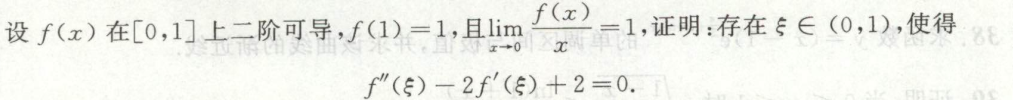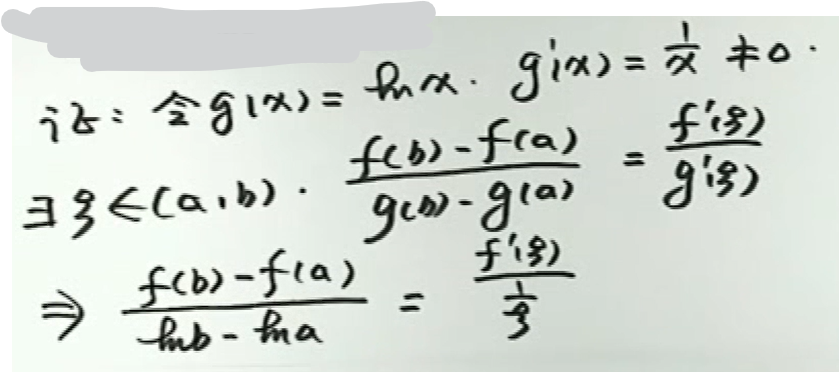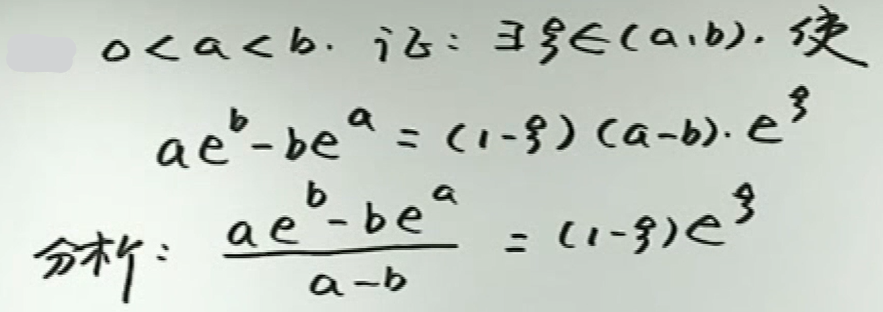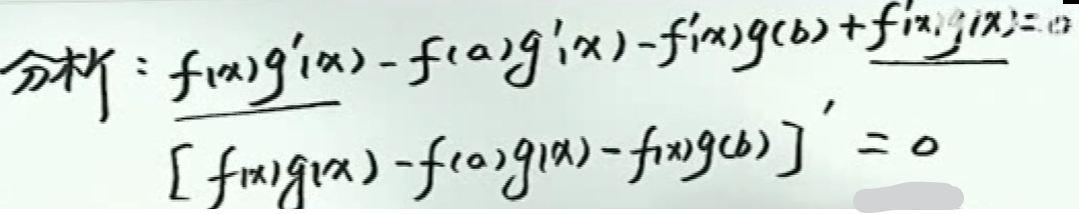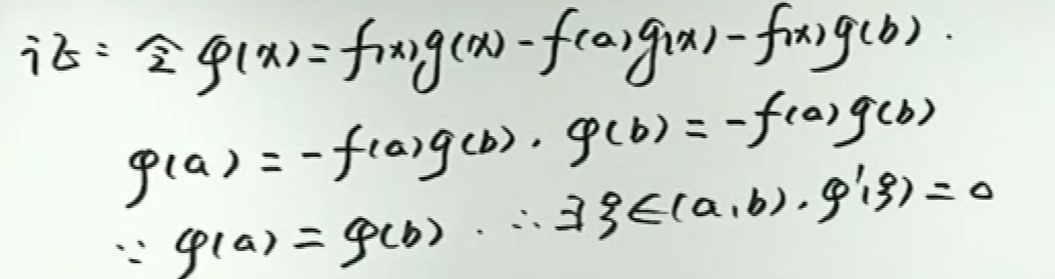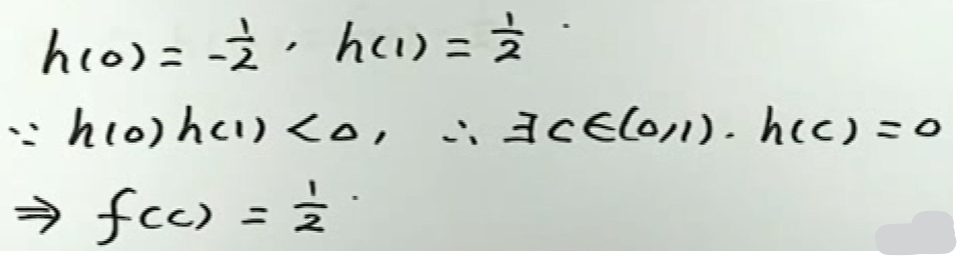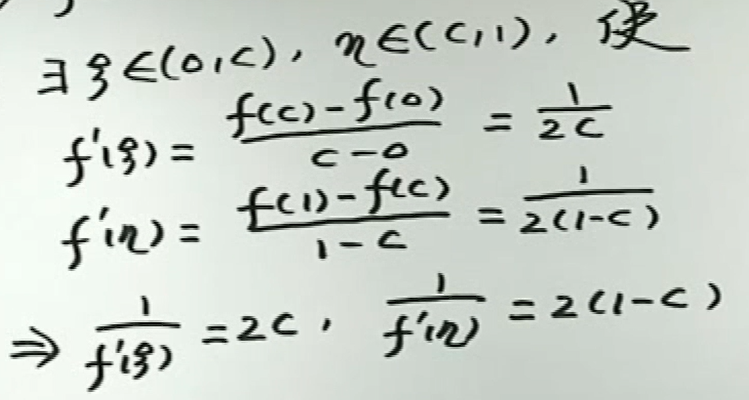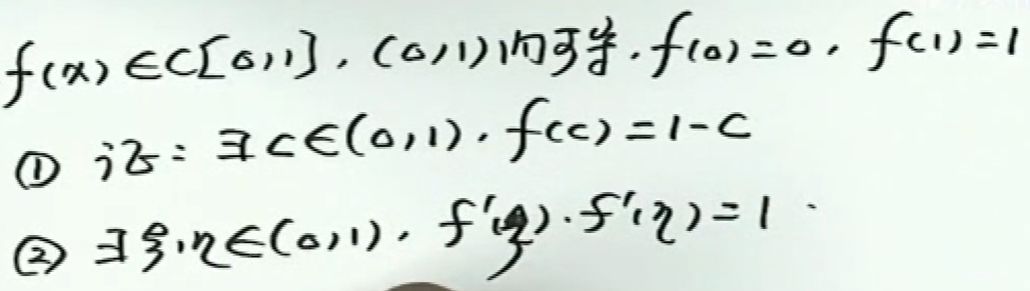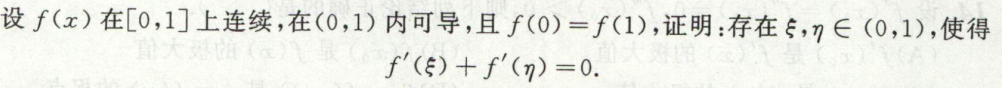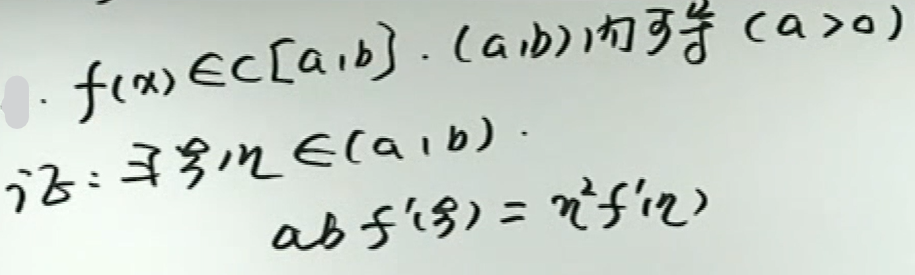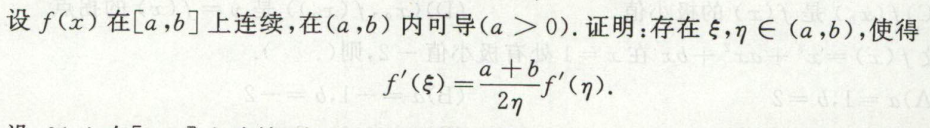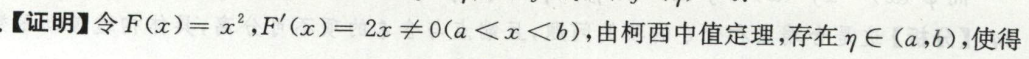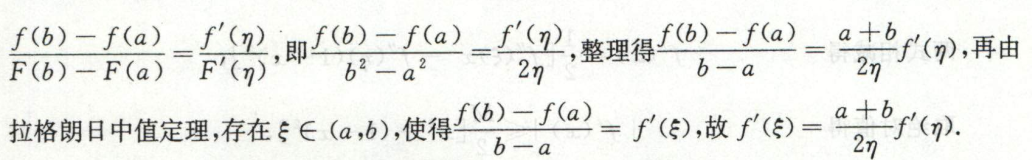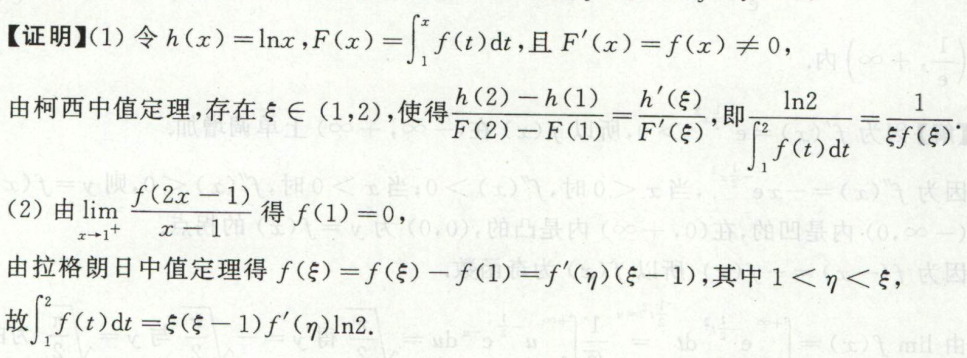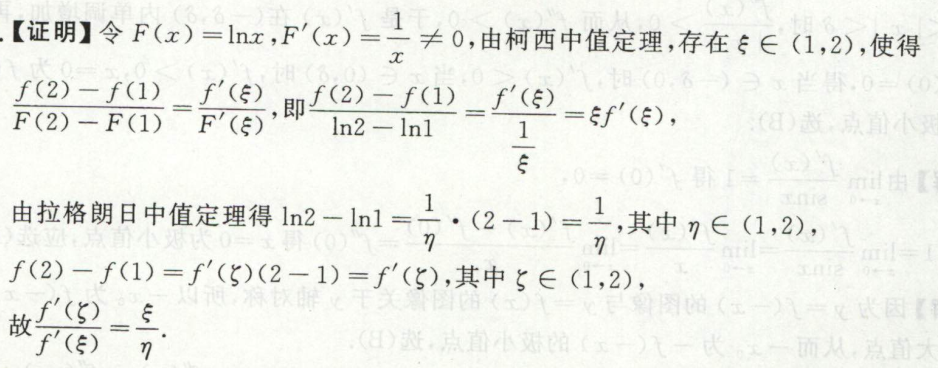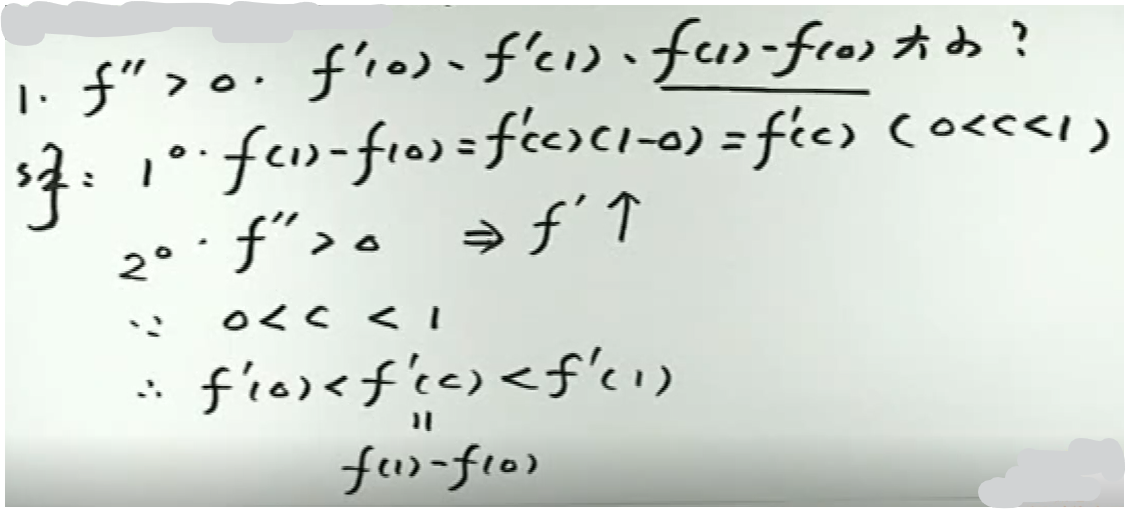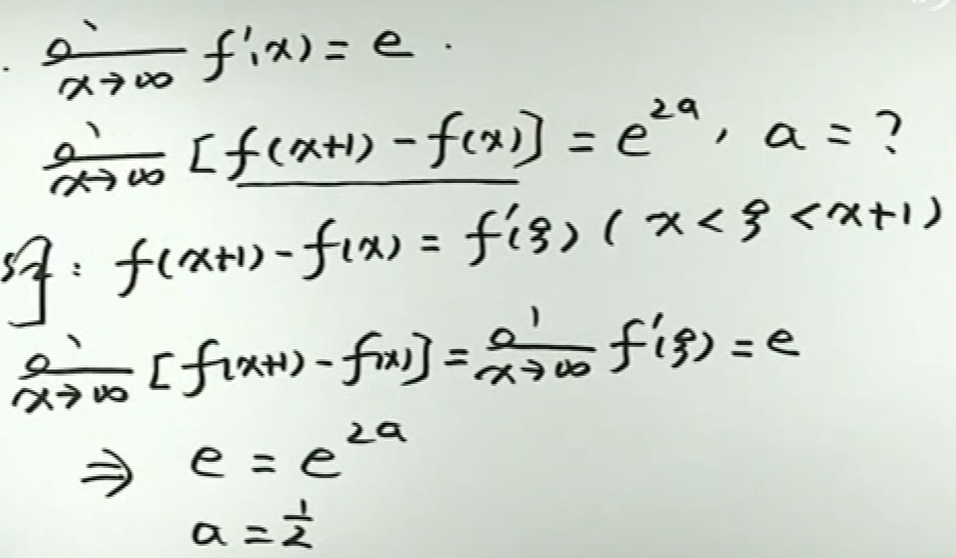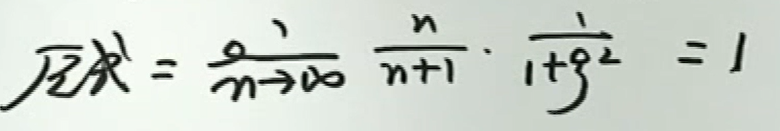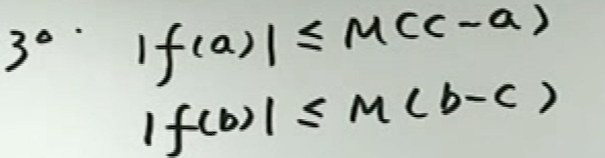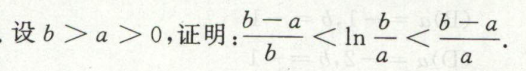高等数学-一元微分学-可导函数的中值定理习题
考察中值定理的定义
考察罗尔定理的定义
例1
image-20200419191223856
image-20200419191114818考察拉格朗日中值定理定义
例1
image-20200419194020246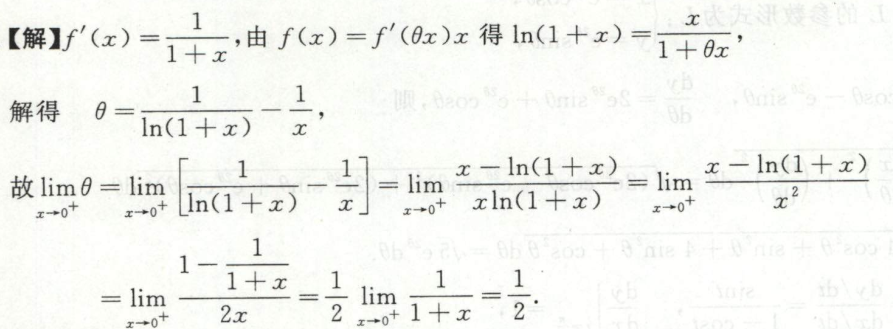
image-20200419194350114例2
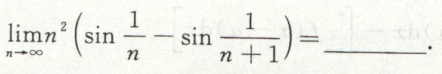image-20200419195057298
image-20200419195136725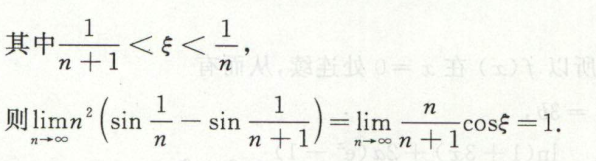
image-20200419195152638例3
image-20200420195449158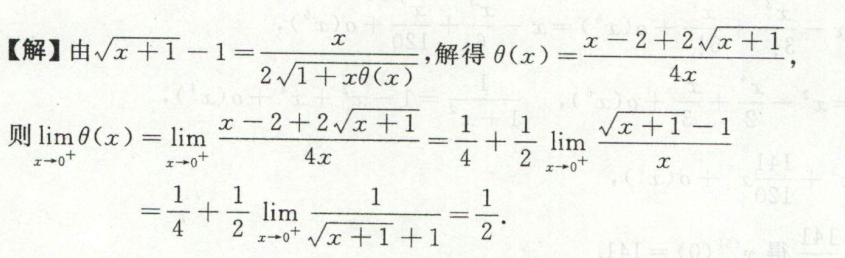
image-20200420195433746其实这道题就是求极限，没考察中值定理
例4
image-20200420224321957
image-20200420224306297例5
image-20200421151721709
image-20200421151648390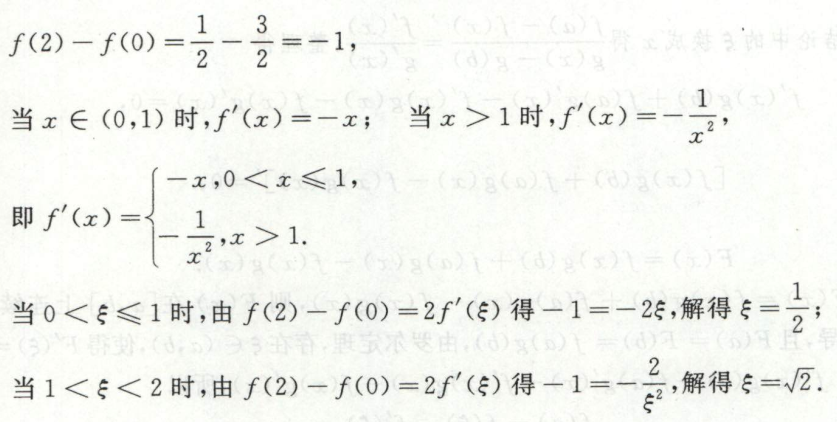
image-20200421151707394例6
image-20200421194140003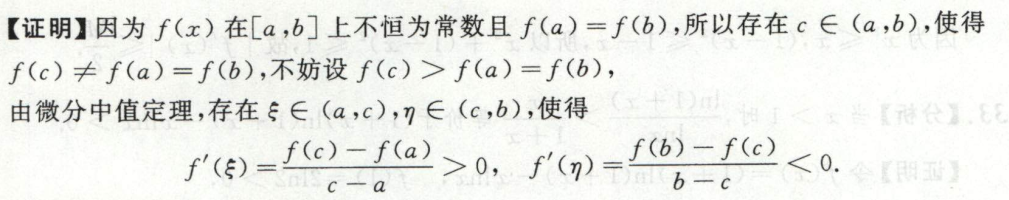
image-20200421194123394例7
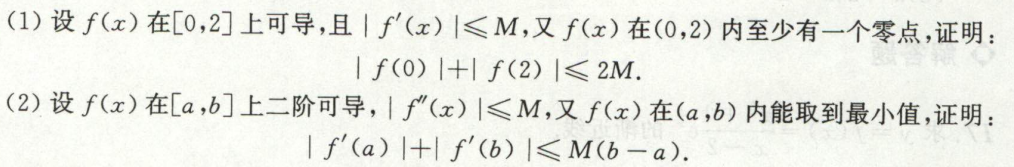image-20200421210050736
image-20200421210034865考察泰勒定理
例1
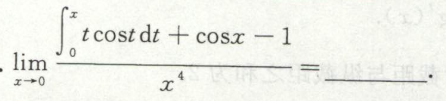image-20200419200751777
image-20200419200728386例2
image-20200420110500021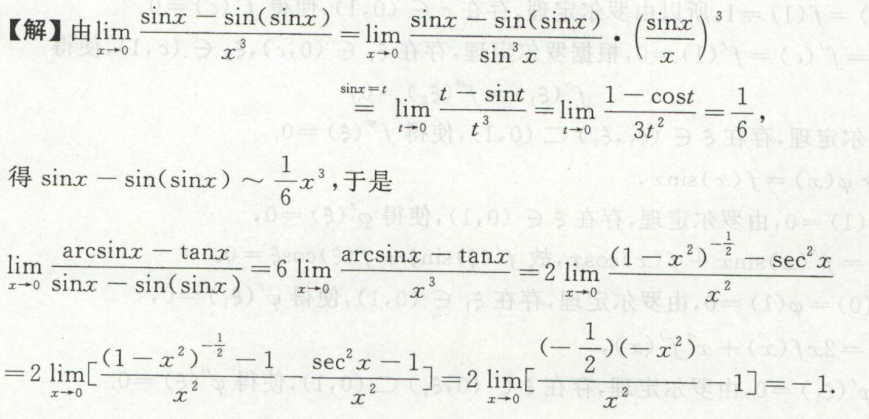
image-20200420110442108分母也可使用泰勒展开替换
例3
image-20200420111856720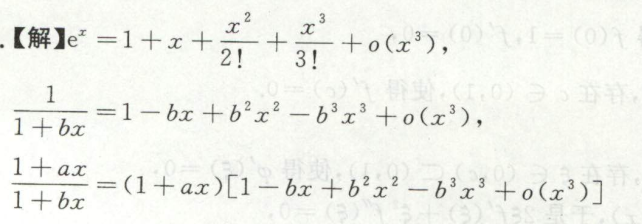
image-20200420111915216
image-20200420111931538其实此题不用泰勒展开，多次使用洛必达法则，也可求出a和b，而且更简单
例4
image-20200420115526420
image-20200420115505603例5
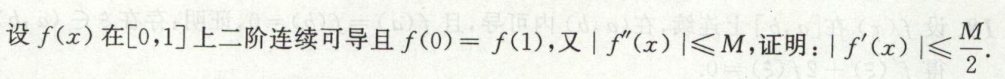image-20200421210709905
image-20200421210619877
image-20200421210647408求证存在\(\xi\)使等式成立
求证\(f^{(n)}(\xi)=0\)
一般会用到罗尔定理
找多个相同值点，多次使用罗尔定理
例1
image-20200417134624096
image-20200417134756621本题使用2次零点定理+罗尔定理证明
例2
image-20200417135300981
image-20200417140421456
image-20200417140650913
image-20200417141636783介值定理+罗尔定理得两个等值点，再用一次罗尔定理证明 函数值相加要想到用介值定理
例3
image-20200417150456153
image-20200417150429213例4
image-20200419225623647
image-20200419225701750例5
image-20200420095404906
image-20200420095349655求证仅含\(\xi\)的等式
即求证仅包含\(\xi\)不包含其他字母的等式
一般方法包括积分还原法和微分方程法
微分中值定理证明题中构造辅助函数的方法
积分还原法求证仅\(\xi\)的等式
左侧可化为\(\frac{f^{\prime}(x)}{f(x)}=[\ln f(x)]^{\prime}\)的式子
一般要求要证的式子包含一个函数及其导数（差一阶），有些可以变换到求证\(\frac{f^{\prime}(x)}{f(x)}=\cdot \cdot \cdot\)的形式，我们可以将左右都看作是函数的导数。
而\(\frac{f^{\prime}(x)}{f(x)}=[\ln f(x)]^{\prime}\)，即证\([\ln f(x)]^{\prime}-[balabala]^{\prime}=0\), 即证\(\{\ln [f(x) \cdot balabala] \}^{\prime}=0\)。
则我们一般可以取辅助函数\(\phi (x) = \ln [f(x) \cdot balabala\)来求证。
例1
image-20200417173651484
image-20200417173758475
image-20200417173938459例2
image-20200417195732919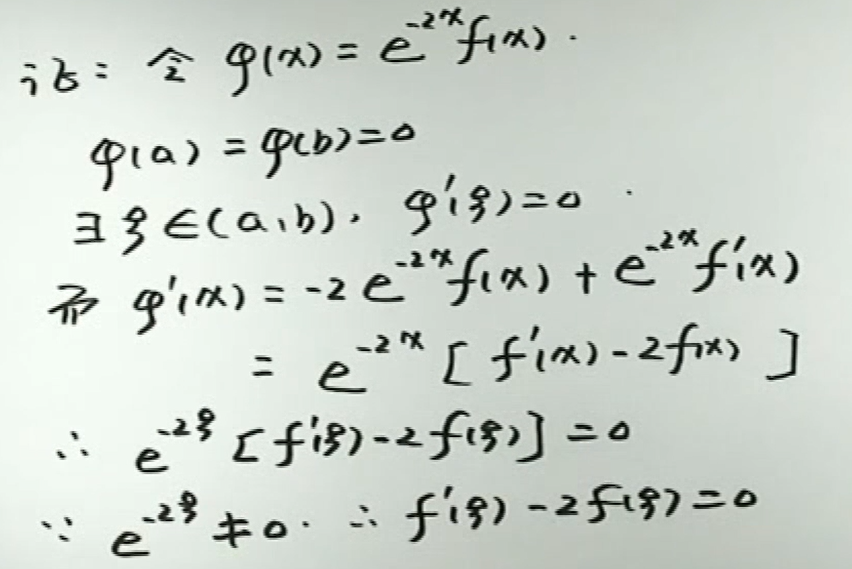
image-20200417195827982例3
image-20200417200632830
image-20200417200930439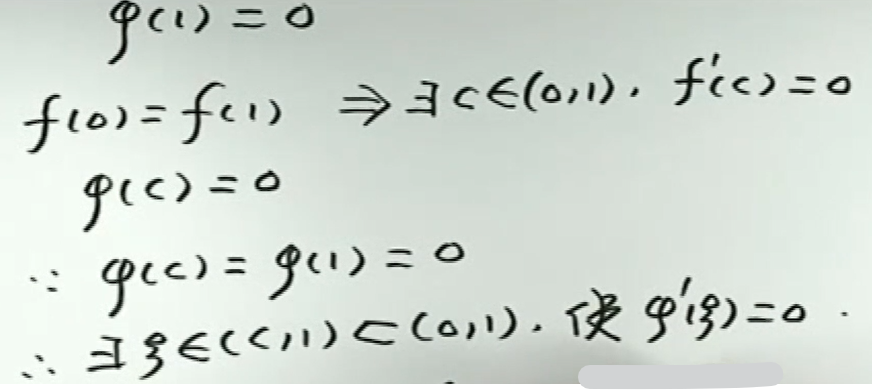
image-20200417201031243
image-20200417201129388例4
image-20200420091719475
image-20200420091737995例5
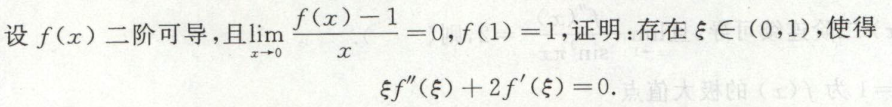image-20200420100144941
image-20200420100203236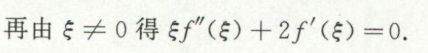
image-20200420100219163例6
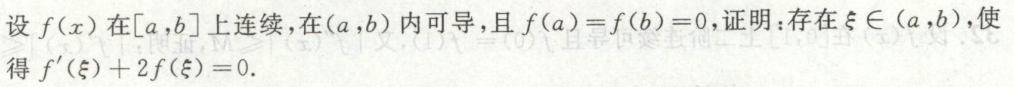image-20200421120216621
image-20200421120237517例7
image-20200421162121240
image-20200421162134466
image-20200421162101282例8
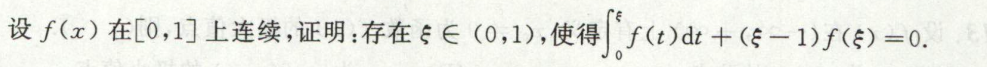image-20200421163921890
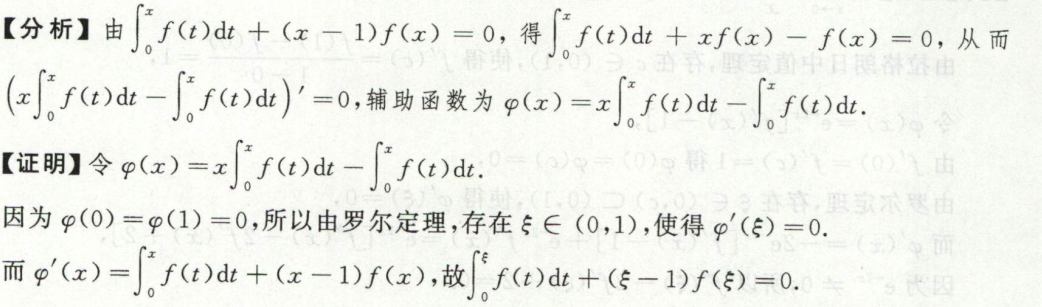image-20200421163905819例9
image-20200422112237034
image-20200422112202616例10
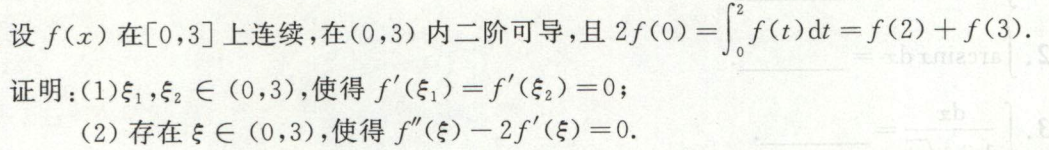image-20200422113633153
image-20200422113714619
image-20200422113734732找其他原函数
变为式子=0的形式，式子左侧作为函数，试着积分，可解的的话，就可作为辅助函数。
例1
image-20200421155838520
image-20200421155825050例2
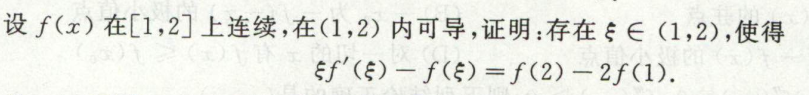image-20200421171654698
image-20200421171619179微分方程法
将要证的方程看作微分方程，解出函数的形式，作为辅助函数。
例1
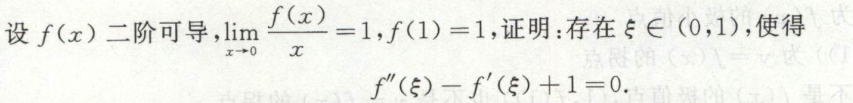image-20200420102643447
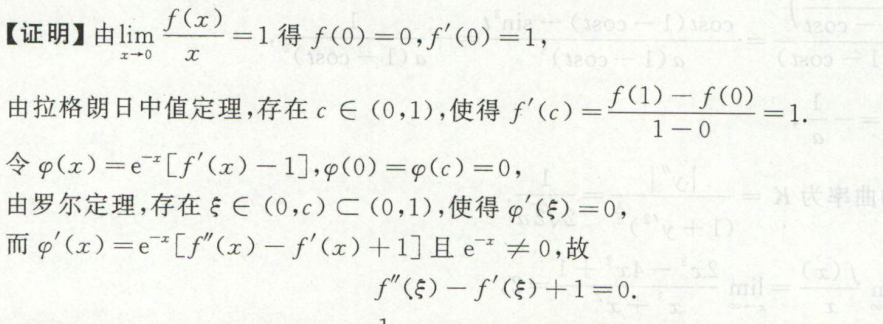image-20200420102659501例2
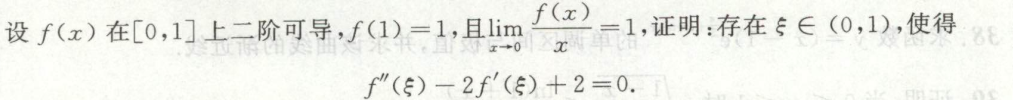image-20200421154812481
image-20200421154745450求证含\(\xi\)和a与b的等式
这里a,b指区间端点，一般是在[a,b]上连续，在(a,b)上可导
a，b与\(\xi\)可分离
若a，b侧有如下形式，则使用对应的方法求解
批注 2020-04-17 201716例1
image-20200417202303061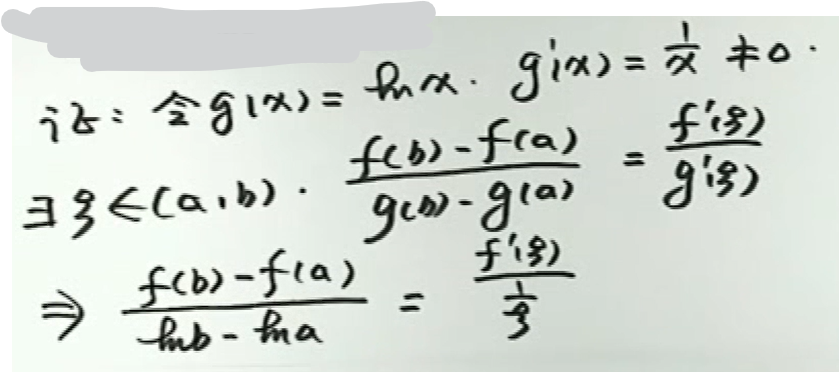
image-20200417202354879例2
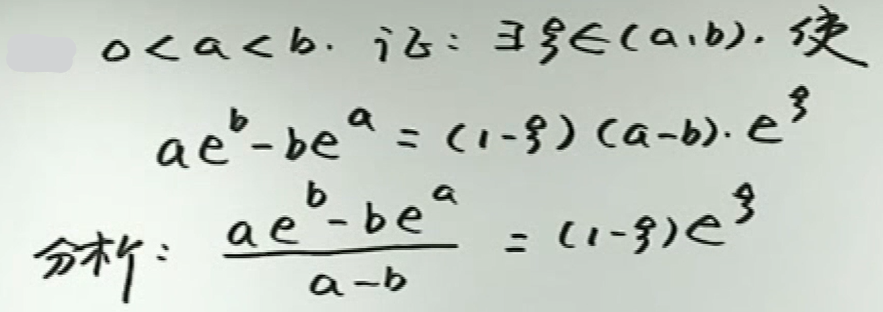image-20200417202625491
image-20200417204213695a，b与\(\xi\)不可分离
\(\xi\)变为x，去分母，移项，变为式子=0, 将其看作(?)'=0，以？部分作辅助函数来证明
例1
image-20200417204924273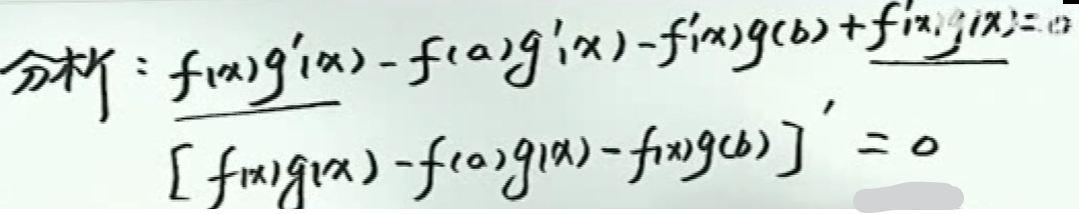
image-20200417205042765
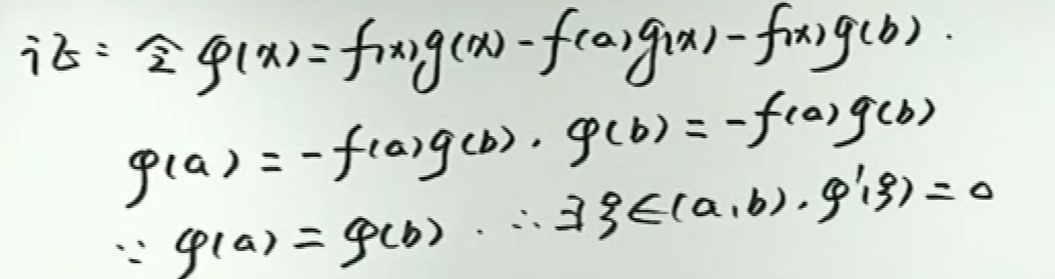image-20200417205218979例2
image-20200421163135029
image-20200421163036916
image-20200421163100435求证存在\(\xi\)和\(\eta\)使等式成立
仅有\(f^{\prime}(\xi), f^{\prime}(\eta)\)
方法是找3个点，使用2次拉格朗日中值定理
例1
image-20200418142509820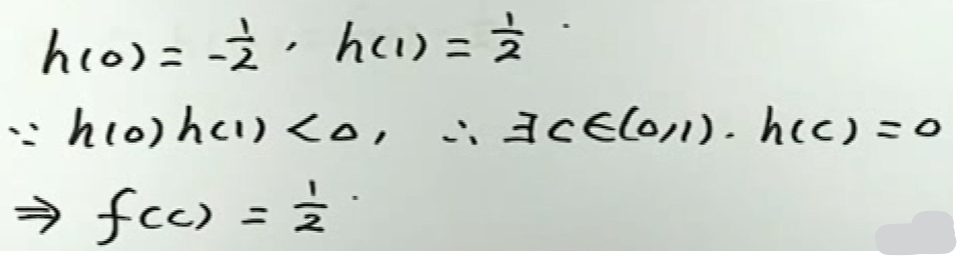
image-20200418143040335
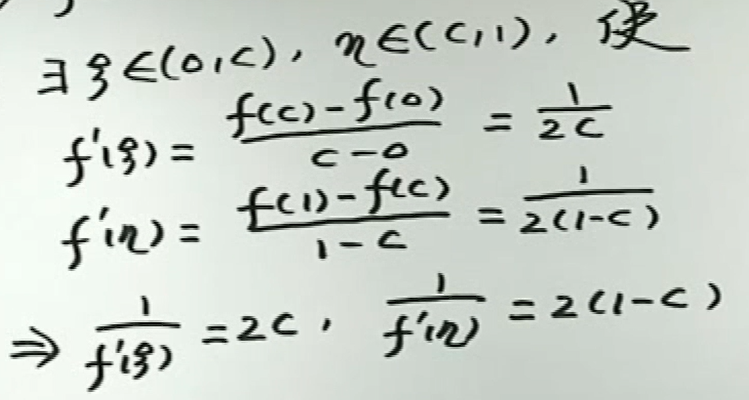image-20200418143150291例2
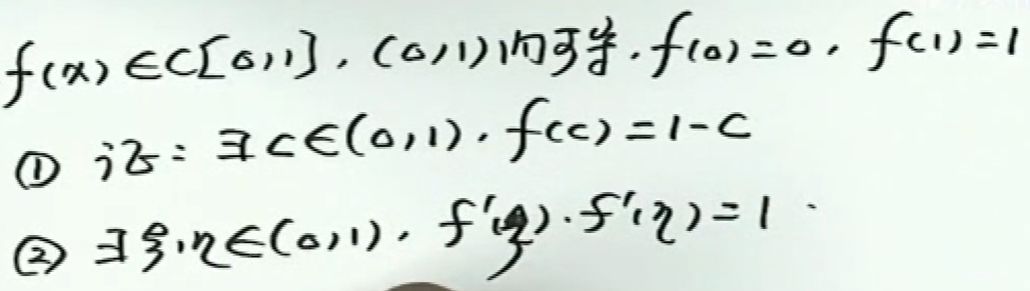image-20200418143719247
image-20200418143808660
image-20200418143844591例3
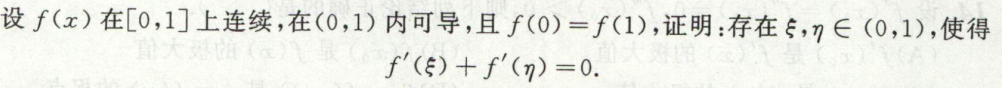image-20200421191400095
image-20200421191417002\(\xi,\eta\)复杂度不同
方法：留下偏复杂一部分，凑成某式的导数，用拉格朗日中值定理；或者凑成连个两个导数的比值，用柯西中值定理。
image-20200418144323608例1
image-20200418144520471
image-20200418144729966
image-20200418144833788例2
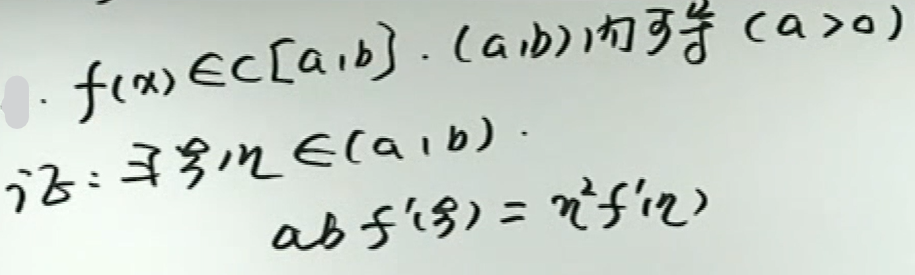image-20200418144932552
image-20200418145022666
image-20200418145124271
image-20200418145212288例3
image-20200420105317475
image-20200420104915669例4
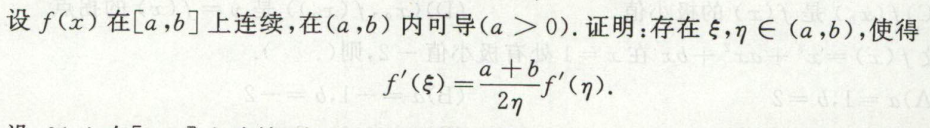image-20200421193128025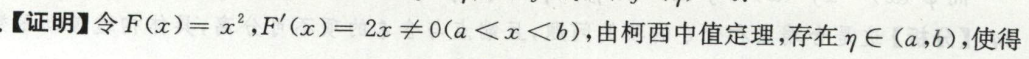
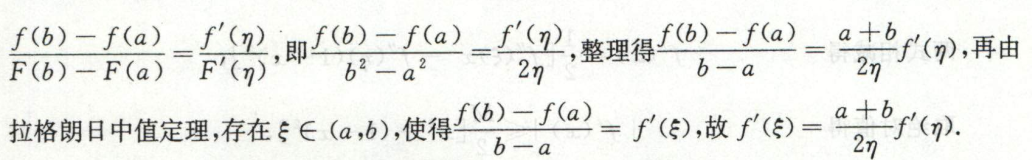
例5
这题第二问要想到使用第一问的结论
image-20200422115052225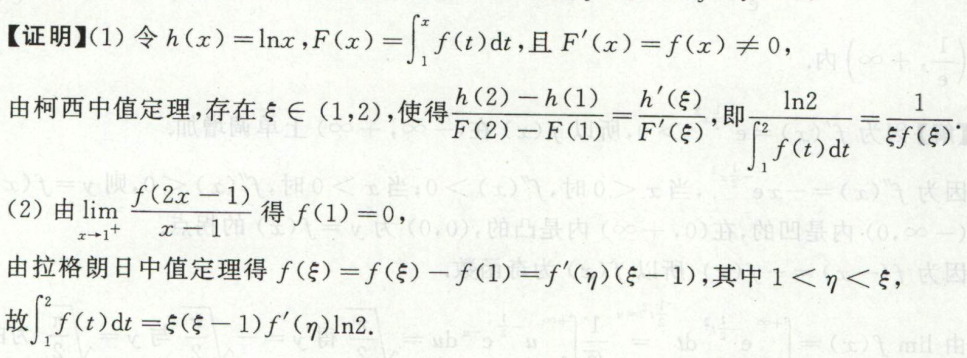
image-20200422115033884求证存在\(\epsilon,\xi,\eta\)使等式成立
例1
image-20200421143911960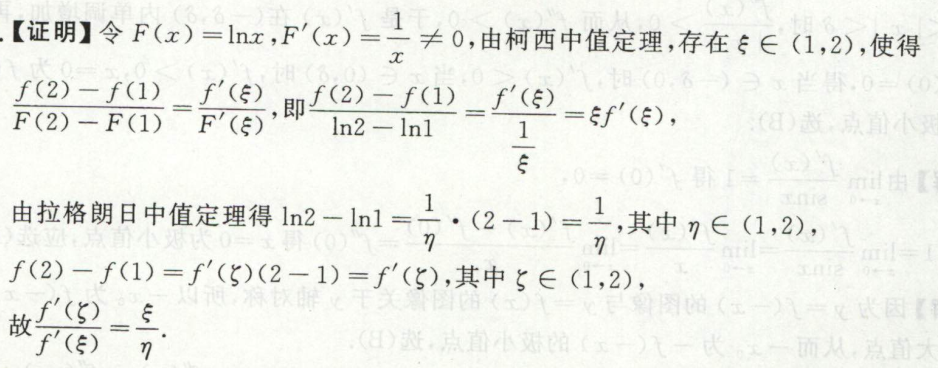
image-20200421143943207拉格朗日中值定理使用
出现\(f(b)-f(a)\)想到使用拉格朗日中值定理
例1
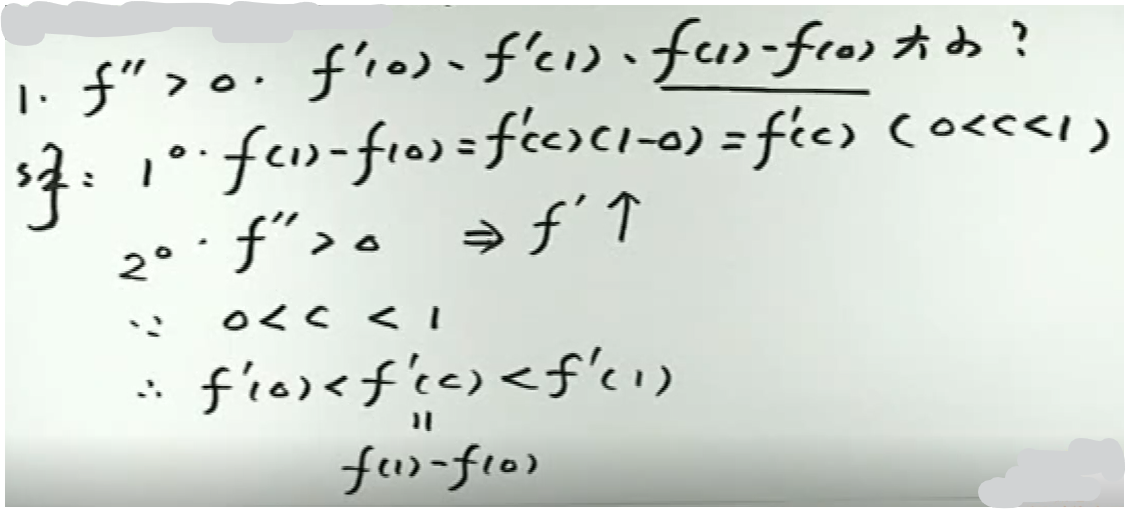image-20200418152102250例2
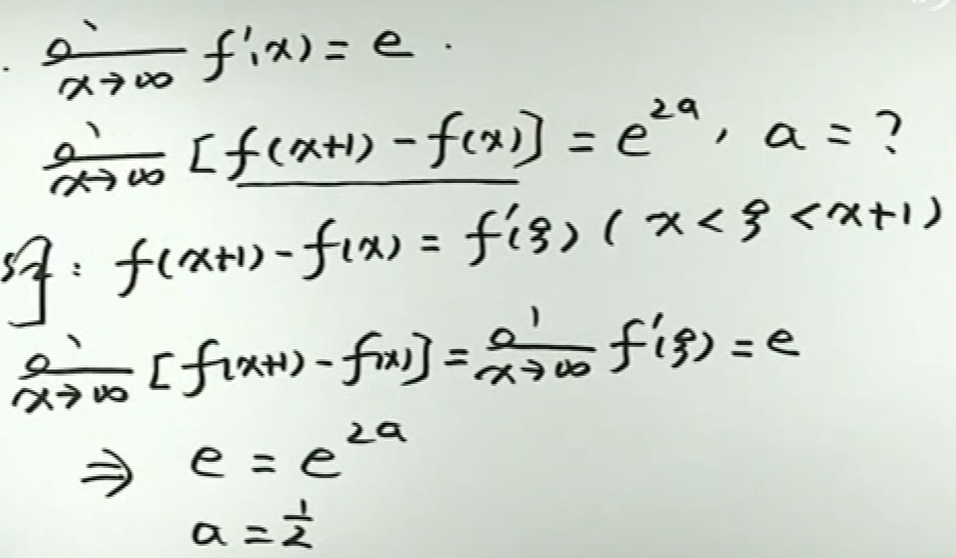image-20200418152203402例3
image-20200418152329175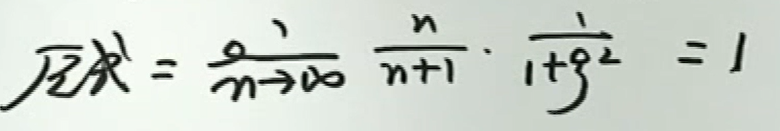
image-20200418152406592出现\(f(a), f(c), f(b)\) 想到使用2次拉格朗日中值定理
例1
image-20200418152916469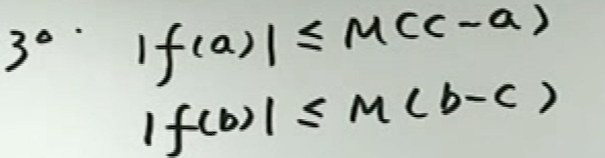
image-20200418155808392例2
image-20200418160135906
image-20200418160302541
image-20200418160344460例3
image-20200419185922277
image-20200419185949907不等式的证明
例1
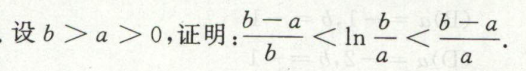image-20200421204048417
image-20200421204128250其实设\(f(x)=x,g(x)=ln(x)\)用柯西中值定理来做也简单。