高等数学-一元微分学-可导函数的中值定理
高等数学-一元微分学-可导函数的中值定理
函数的导数分类
函数的导数分为4种情况,导数大于0,等于0,小于0,不可导
可导的局部特性
以导数大于0为例,根据函数极限的局部保号性:
\(\begin{aligned} if \quad & f^{\prime}(a)>0 ,f^{\prime}(a) =\lim_{x \rightarrow a} \frac{f(x)-f(a)}{x-a}>0 \\ \Rightarrow \quad& \exists \delta>0, x<|x-a|<\delta , \frac{f(x)-f(a)}{x-a}>0 \end{aligned}\)
即导数大于0,表示在极小邻域内,函数值递增 同理,导数小于0,表示在极小邻域内,函数值递减 同理,导数等于0,表示在极小邻域内,函数取极值
费马定理
函数在某点及邻域有定义,在该点取极值,在该点导数存在 \(\Rightarrow\) 该点导数为0(该点是驻点)。
即有:
\(f(x)\)在\(x=a\)取极值, \(\Rightarrow \nLeftarrow\) \(f'(a)=0\) 或 不存在\(f'(a)\)
\(f(x)\)可导且在\(x=a\)取极值, \(\Rightarrow \nLeftarrow\) \(f'(a)=0\)
可导函数的中值定理
几个中值定理的共同条件:一个函数在闭区间连续,开区间可导,中间存在一个点怎么怎么样
高阶中值定理(拉格朗日余项泰勒定理)的条件:一个函数在闭区间n阶连续,开区间n+1阶可导,中间存在一个点怎么怎么样
罗尔定理
若\(f(x)\)在闭区间\([a, b]\)内连续,在开区间\((a, b)\)内可导,且\(f(a)=f(b)\),则至少存在一点\(\xi \in(a, b)\),\(f^{\prime}(\xi)=0\)

拉格朗日中值定理
若\(f(x)\)在闭区间\([a, b]\)内连续,在开区间\((a, b)\)内可导,且\(f(a)=f(b)\),则至少存在一点\(\xi \in(a, b)\),\(f(b)-f(a)=f^{\prime}(\xi)(b-a)\)

作辅助函数+罗尔定理可证此定理; 所作的辅助函数:直线AB-曲线AB,则在端点处都为0,满足罗尔定理条件。
柯西中值定理
若\(f(x), g(x)\)在闭区间\([a, b]\)连续,在开区间\((a, b)\)可导,且\(g^{\prime}(x) \neq 0, x \in(a, b)\)则至少存在一点\(\xi \in(a, b)\),使得\(\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime}(\xi)}{g^{\prime}(\xi)}\)。
作辅助函数+罗尔定理证明
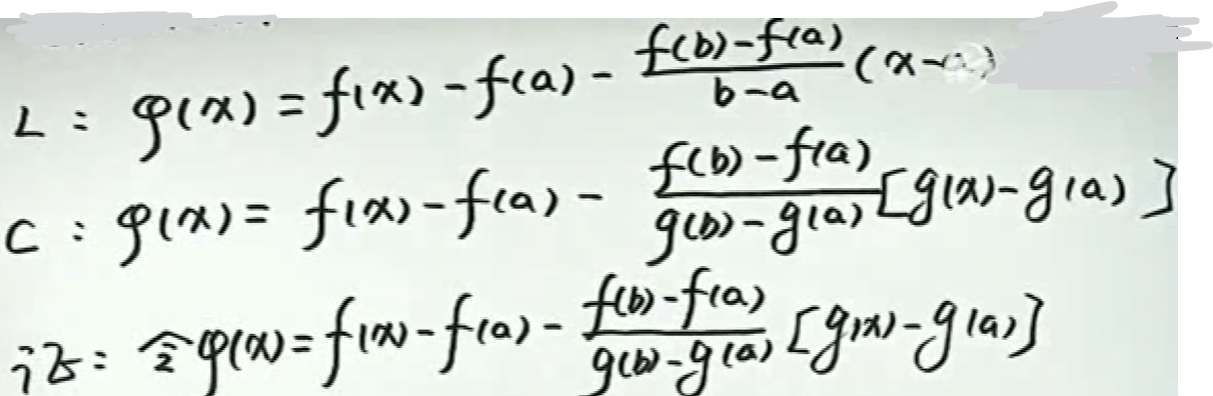
泰勒定理
泰勒定理一般有两种形式。
具有拉格朗日余项的n阶泰勒公式,可看作是高阶中值定理。退化到零阶,即拉格朗日中值定理。
佩亚诺余项泰勒公式,余项是无穷小,一般用于无穷小的比较(比如求极限)
具有拉格朗日余项的n阶泰勒公式
设\(f(x)\)在闭区间\([a,b]\)上有n阶连续导数,在开区间\((a,b)\)内有n+1阶导数,\(x_{0} \in[a, b], x \in[a, b]\)是任意两点,则至少存在一点\(\xi\)介于x和\(x_0\)之间,使得\(f(x)=f\left(x_{0}\right)+\frac{f^{\prime}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{x}(x)\),其中\(R_{n}(x)=\frac{f^{(n+1)}(\xi)}{(n+1) !}\left(x-x_{0}\right)^{n+1}\)称为拉格朗日余项,整个公式称为具有拉格朗日余项的n阶泰勒公式。
若\(x_0 = 0\),则该公式称为麦克劳林公式。
| 函数 | 对应的麦克劳林级数展开 |
|---|---|
| \(\frac{1}{\sqrt{1-x^{2}}}=\left(1-x^{2}\right)^{-\frac{1}{2}}\) | \(1+\sum_{n=1}^{\infty} \frac{1 \times 3 \times 5 \times \cdots \times(2 n-1)}{2^{n} \cdot n !} x^{2 n}\) |
| \(\frac{1}{1+x^{2}}\) | \(1-x^{2}+x^{4}-x^{6}+\cdots+(-1)^{n} x^{2 n}+\cdots\) |
| \(\frac{1}{x-1}=-\frac{1}{1-x}\) | \(-\sum_{n=0}^{\infty} x^{n}\) |
| \(\frac{1}{2 x-1}=-\frac{1}{1-2 x}\) | \(-\sum_{n=0}^{\infty} 2^{n} x^{n}\) |
| \(\arctan x\) | \(\begin{array}{ll}=x-\frac{1}{3} x^{3}+\frac{1}{5} x^{5}-\cdots+(-1)^{n} \frac{x^{2 n+1}}{2 n+1}+\cdots & (-1 \leqslant x \leqslant 1) \\ =\sum_{n=0}^{\infty}(-1)^{n} \frac{x^{2 n+1}}{2 n+1} & (-1 \leqslant x \leqslant 1)\end{array}\) |
佩亚诺余项泰勒公式
将定理的条件减弱为: 设\(f(x)\)在\(x=x_0\)具有n阶导数,设x为\(x_0\)充分小邻域内的任意一点,则有\(f(x)=f\left(x_{0}\right)+\frac{f^{\prime}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\cdots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{n}(x)\),其中\(R_{n}(x)=o\left(\left(x-x_{0}\right)^{n}\right)\),整个公式称为佩亚诺余项泰勒公式。
常见的泰勒公式(佩亚诺余项式)

已知函数可导证明不等式
前提条件:设\(f(x)\)与\(g(x)\)在区间\((a,b)\)可导 用微分学证明不等式:在此区间内\(f(x) \geqslant g(x)\)或者\(f(x)>g(x)\)
先命\(\varphi(x)=f(x)-g(x)\),然后用下列方法之一或者联合运用来证明
用单调性证明
若\(\varphi(x)=f(x)-g(x)\)单调增加,且左端点处值大于等于0,则\(\varphi(x)=f(x)-g(x) \ge 0\)恒成立。 同理可证其他情况。

用最值证明
若在\((a,b)\)内,\(\varphi (x)\)有最小值大于0,则在\((a,b)\)内恒有\(\varphi (x) \gt 0\). 若\(\varphi (x)\)有最小值等于0则在\((a,b)\)内恒有\(\varphi (x) \ge 0\)。
类似可用最大值可证小于,小于等于的情况。
用拉格朗日中值公式证明
如果题目求证\(f(b)-f(a)>A(b-a)\),常想到拉格朗日中值定理:\(f(b)-f(a)=f^{\prime}(\xi)(b-a)\)。 只要去证\(f^{\prime}(\xi)>A\),则原式得证。
同理可证\(f(b)-f(a)<A(b-a)\)
用拉格朗日余项泰勒公式证明
如果\(f^{\prime \prime}(x)\)存在且(大于0或者小于0),想到1阶拉格朗日余项泰勒公式:\(f(x)=f\left(x_{0}\right)+\frac{1}{1!} f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{1}{2 !} f^{\prime \prime}(\xi)\left(x-x_{0}\right)^{2}\)。 证明的关键是展开位置\(x_0\)的确定。
如果\(f^{\prime \prime}(x)\)存在且(大于0或者小于0),也可能使用两次拉格朗日中值定理(0阶拉格朗日余项泰勒公式):\(f(x)=f\left(x_{0}\right)+\frac{1}{1!} f^{\prime}\left(\xi\right)\left(x-x_{0}\right)\)
如果为更高阶导数存在(且大于0或小于0),那么想到将\(f(x)\)展开至更高阶。
存在零点及零点个数的证明
零点是否存在的证明
由连续函数介值定理或零点定理证明
由罗尔定理证明
罗尔定理关于零点的推论:设以下所提到的导数存在,则有结论:如果\(f(x)\)有\(k(k\ge 2)\)个零点,则\(f^\prime (x)\)至少有(k-1)个零点,…,\(f^{(k-1)}(x)\)至少有1个零点。
至多有几个零点的证明
设以下所提到的导数存在,则有结论: 如果\(f^{\prime}(x)\)没有零点,则\(f(x)\)至多有1个零点; 如果\(f^{\prime}(x)\)最多1个零点,则\(f(x)\)至多有2个零点; 如果\(f^{\prime}(x)\)最多k个零点,则\(f(x)\)至多有k+1个零点; 如果\(f^{\prime \prime}(x)\)没有零点,则\(f^{\prime}(x)\)最多1个零点,\(f(x)\)最多2个零点。。。。