高等数学-一元微分学-导数的应用-单调性与极值
高等数学-一元微分学-导数的应用-单调性与极值
单调性与极值
取得极值求参数
例1
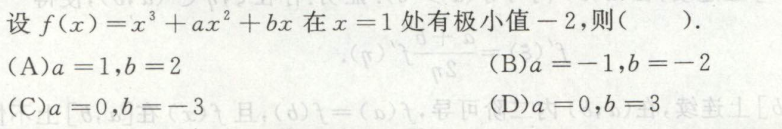

求函数极值最值拐点
例1

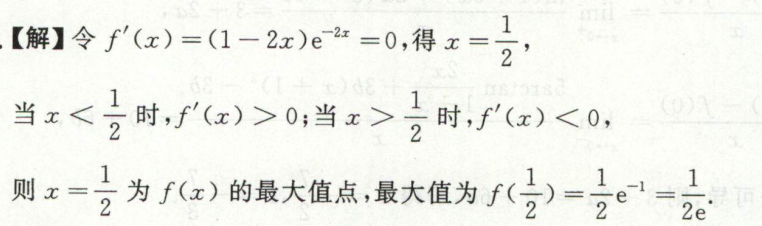
例2


例3


例4

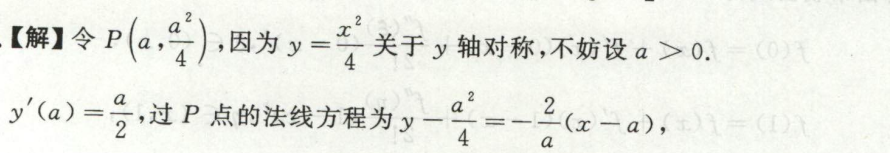

例5


不等式的证明
例1
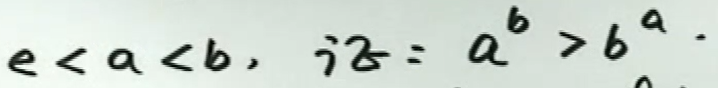

例2


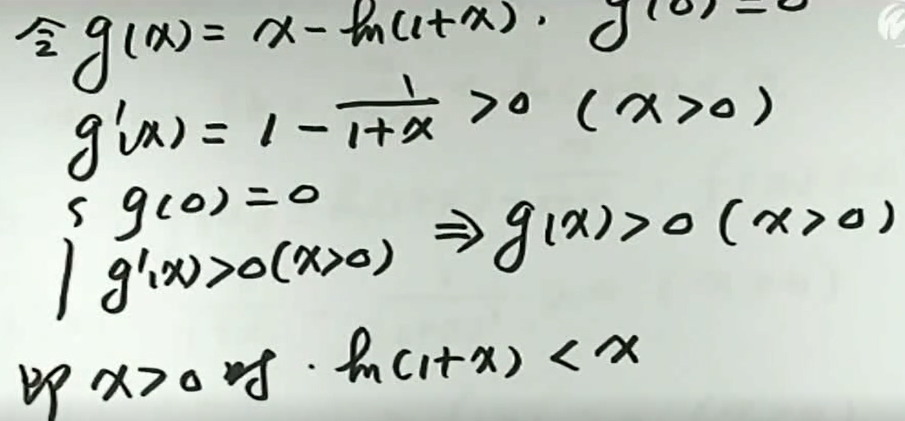
例3
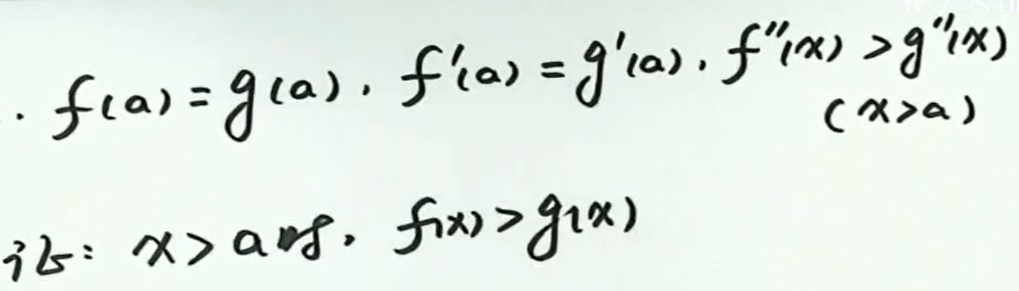


例4
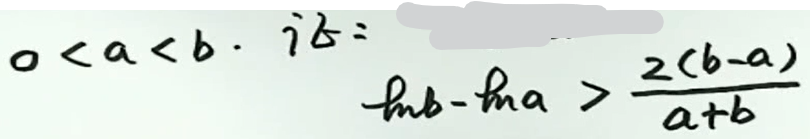
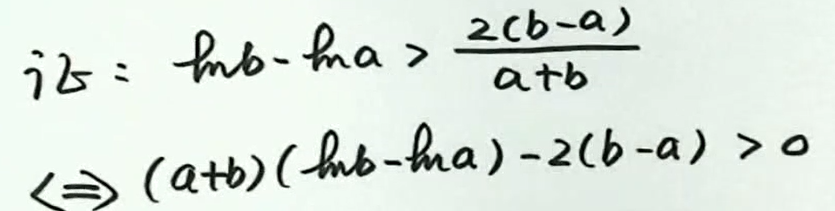
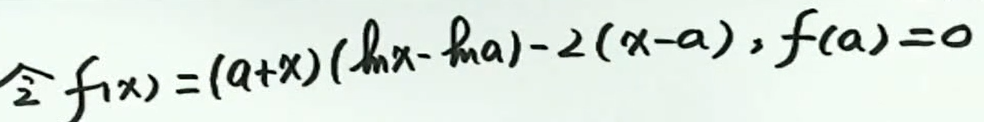
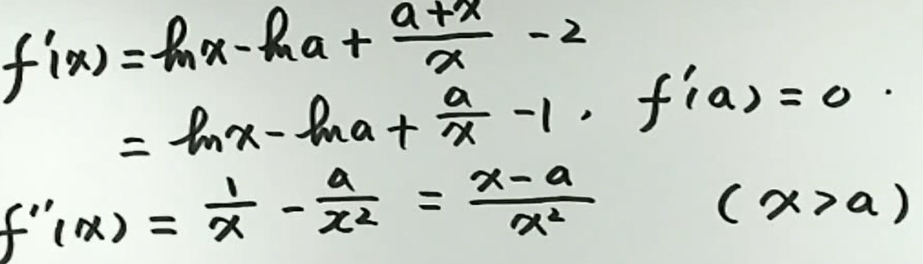

例5


例6
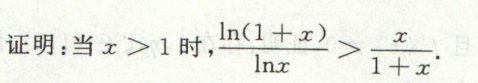

例7


例8


例9


例10


例11


方程根的讨论
零点定理证明方程有根
例1

罗尔定理加原函数证明方程有根

例1

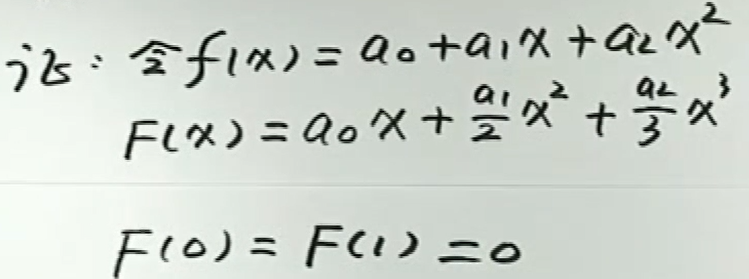

单调法求方程根的数目
- 设立函数,关注定义域
- 找出驻点和不可导点,考察这些点处的值
- 关注区间两侧,做草图
例1

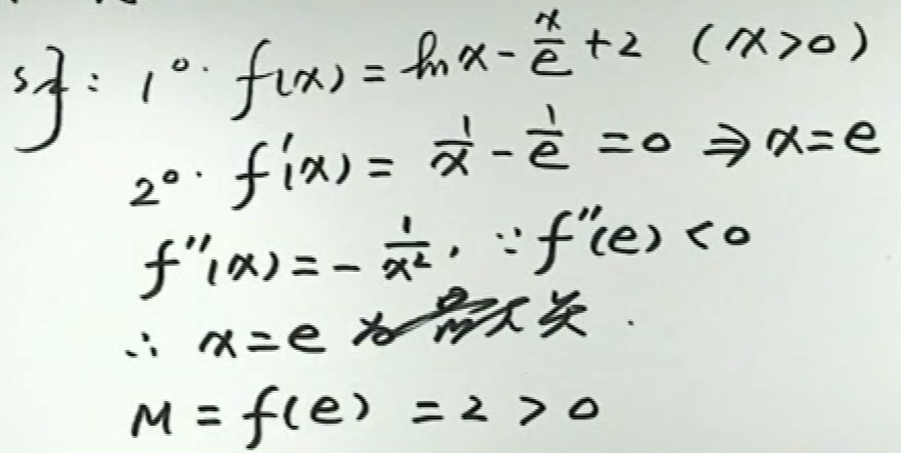
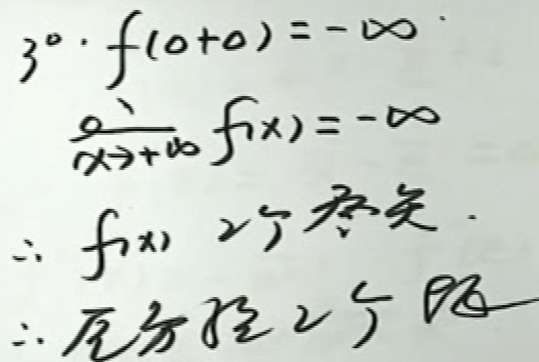
例2



例3
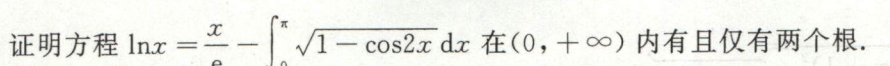
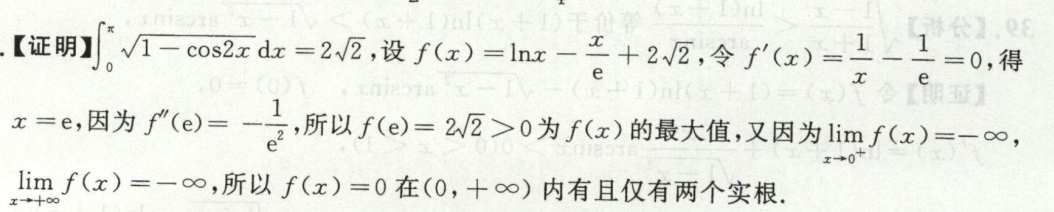
例4
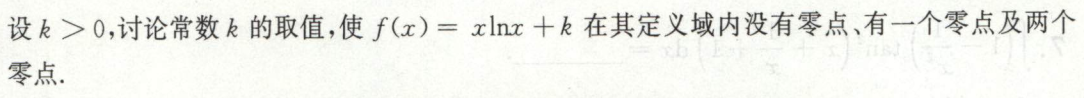
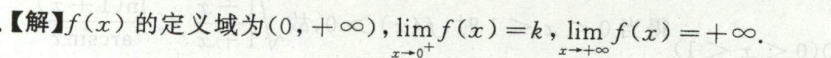

例5
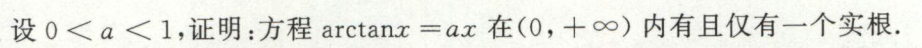

已知方程根数目求参数的范围
例1
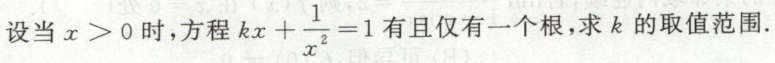

例2


函数极值点的判定
- 设立函数,关注定义域
- 找出驻点和不可导点
- 极值点的判别法
- 第一判别法:一阶导数左边大于0右边小于0,极大值
- 第二判别法:二阶导数小于0,极大值
例1



例2




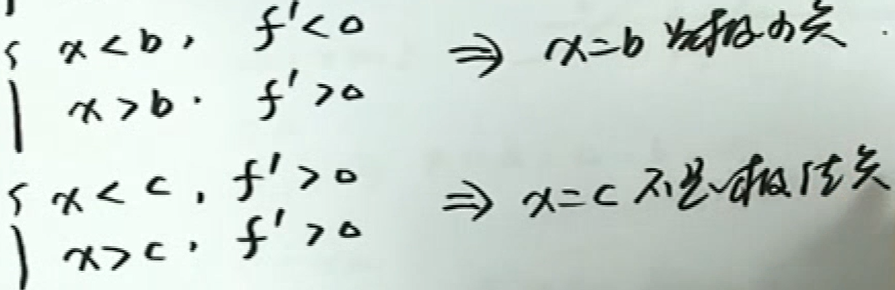
例3

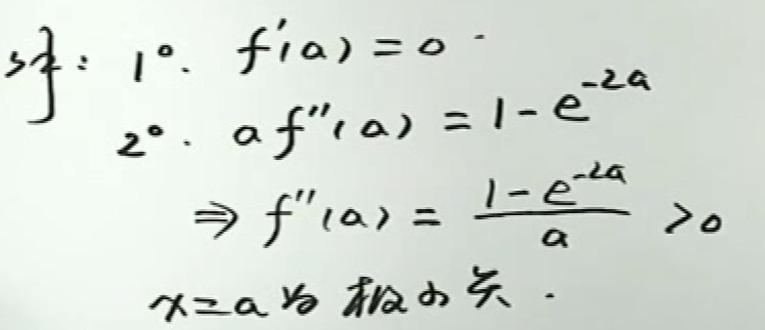
例4


例5


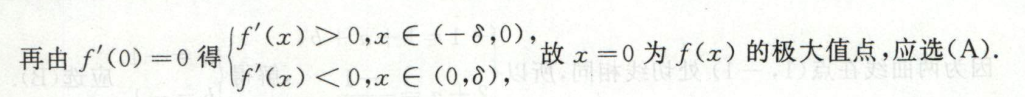
例6
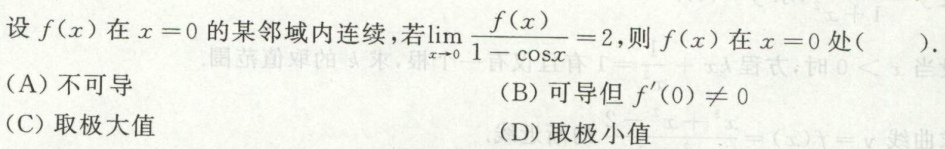

例7
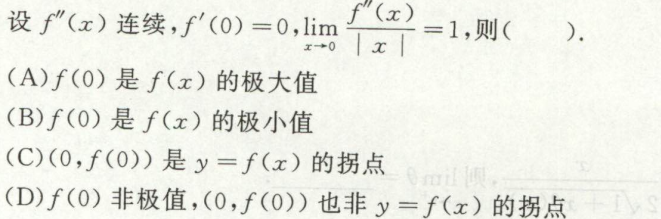

例8
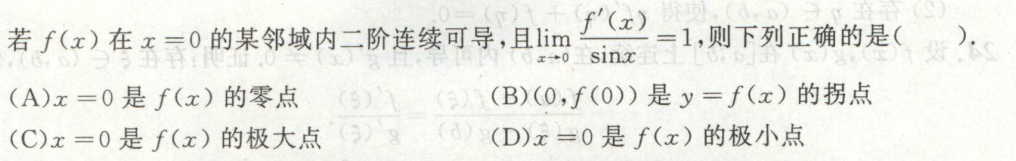

例9


凹凸性或拐点的判定
二阶导数与0的比较判断凹凸性
例1
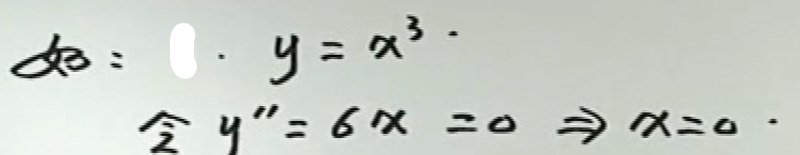
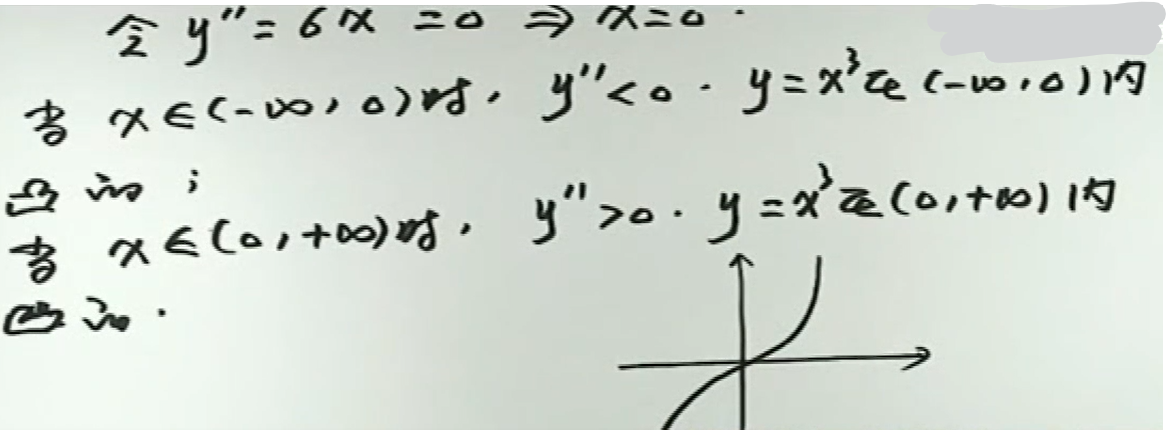
例2



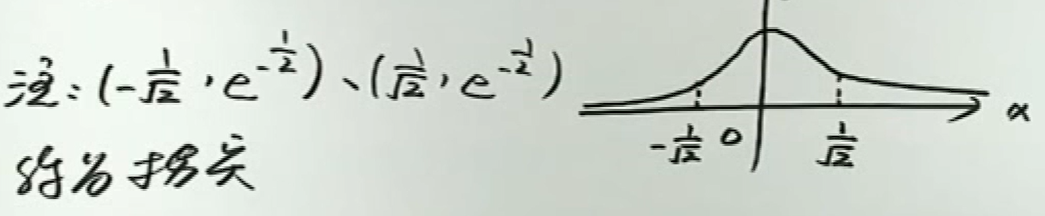
例3


同理,x1,x2也是拐点
例4


例5
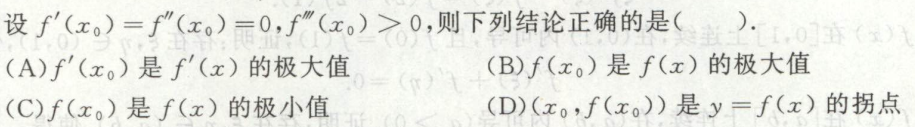

例6
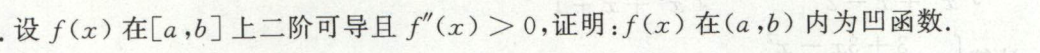

求函数渐近线
例1
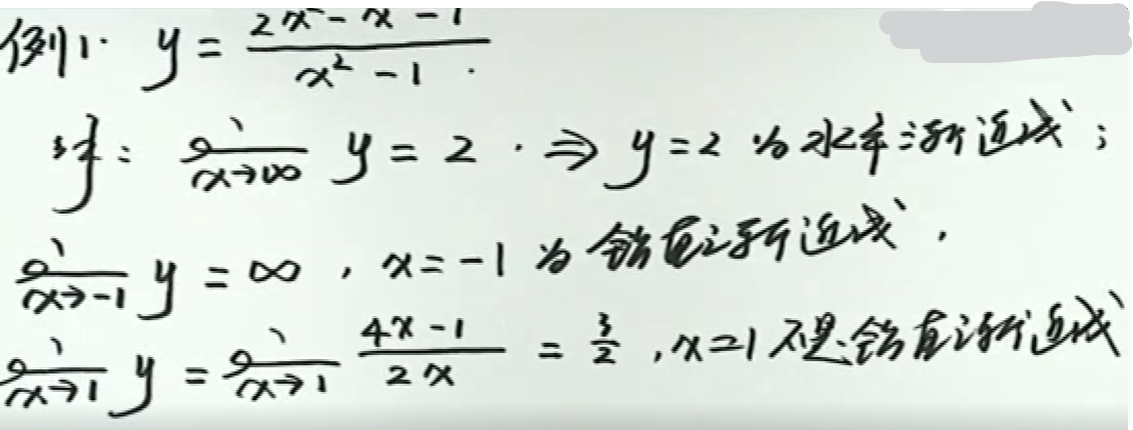
例2

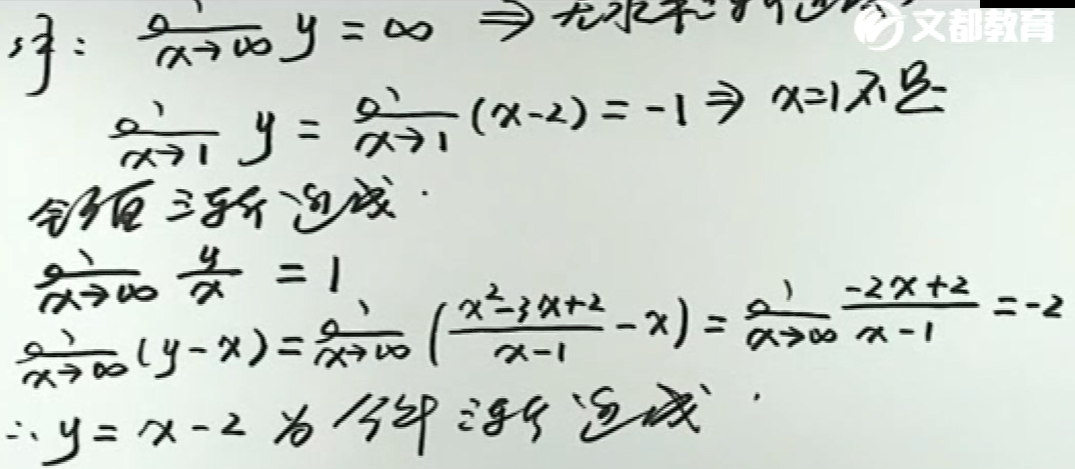
例3
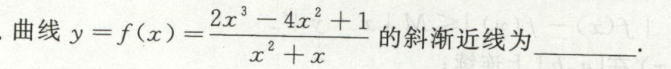
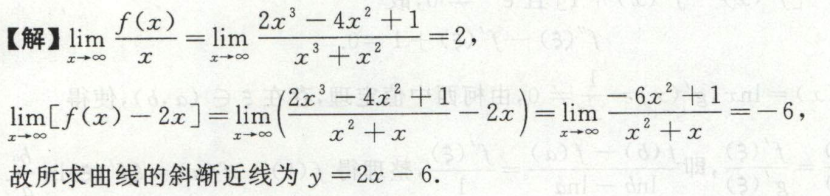
例4


例5


例6
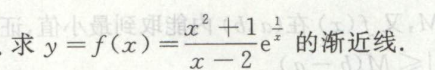

例7


例8

