高等数学-一元微分学-导数的应用

弧微分与曲率

弧微分

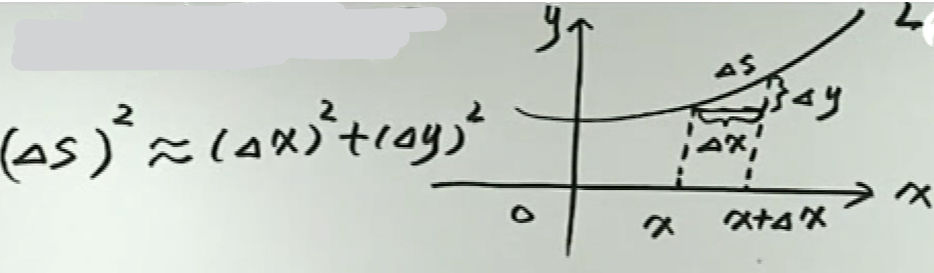
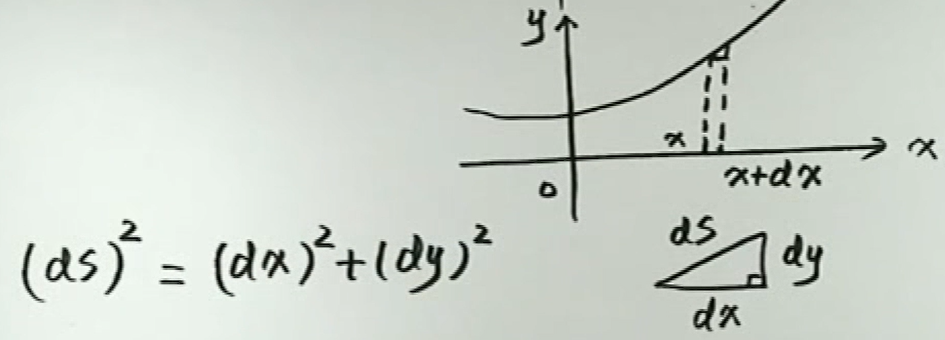
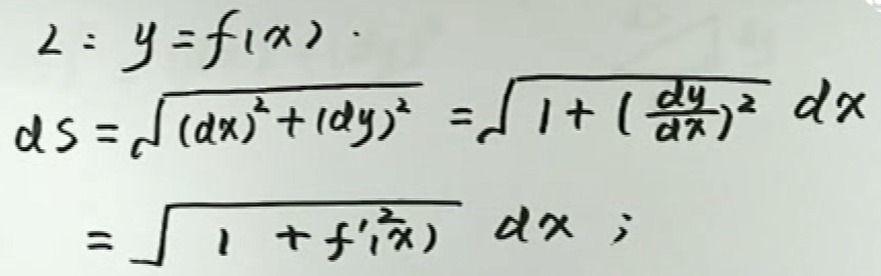
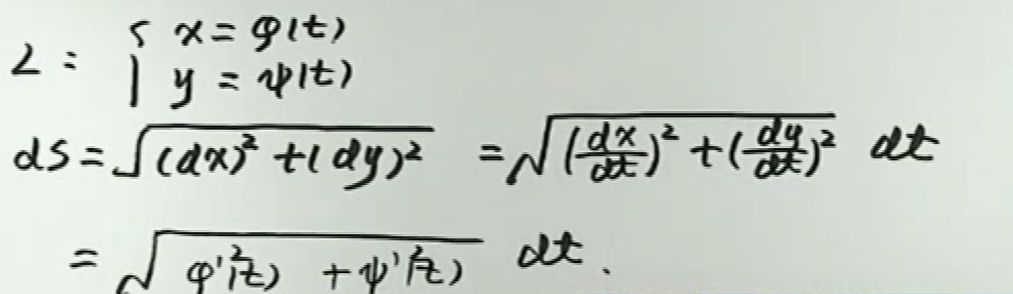
直角座标系中，\(\mathrm{d} s=\sqrt{1+y^{\prime 2}} \mathrm{d} x,(\mathrm{d} x>0)\)

参数方程中，\(\mathrm{d} s=\sqrt{x^{\prime 2}(t)+y^{\prime 2}(t)} \mathrm{d} t,(\mathrm{d} t>0)\)

极坐标系中，\(\mathrm{d} s=\sqrt{p^{2}(\theta)+p^{\prime}(\theta)^{2}} \mathrm{d} \theta,(\mathrm{d} \theta>0)\)

极坐标系中的证明： \(r=r(\theta)\) \(x=r \cos \theta, y=r \sin \theta\) \(\frac{d x}{d \theta}=\frac{\partial x}{\partial r} \frac{d r}{d \theta}+\frac{\partial x}{\partial \theta}=\cos \theta r^{\prime}-r \sin \theta\) \(\frac{d y}{d \theta}=\frac{\partial y}{\partial r} \frac{d r}{d \theta}+\frac{\partial y}{\partial \theta}=\sin \theta r^{\prime}+r \cos \theta\) \(d s=\sqrt{\left(\frac{d x}{d \theta}\right)^{2}+\left(\frac{d y}{d \theta}\right)^{2}} d \theta=\sqrt{r^{2}+r^{\prime}(\theta)^{2}} d \theta\)

曲率

曲率的引入

在数学上，曲线的曲率表明曲线在某一点的弯曲程度的数值。

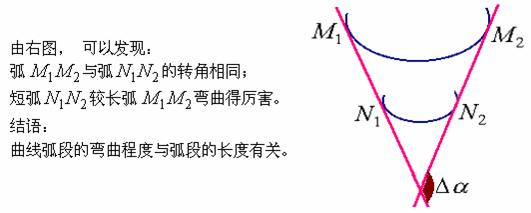
曲率越大，表示曲线的弯曲程度越大。

曲率定义

比值\(\left|\frac{\Delta \alpha}{\Delta s}\right|\)表示单位弧段上的切线转角，刻划了弧MM’的平均弯曲程度。称它为弧段MM’的平均曲率。记作\(\bar{k}=\left|\frac{\Delta \alpha}{\Delta s}\right|\)

当时(即：\(M^{\prime} \rightarrow M\))，上述平均曲率的极限就称着曲线在点M处的曲率，记作\(k=\lim _{\Delta s \rightarrow 0}\left|\frac{\Delta \alpha}{\Delta s}\right|\) 。¹

当\(\lim _{\Delta s \rightarrow 0} \frac{\Delta \alpha}{\Delta s}=\frac{d \alpha}{d s}\)存在时，有 \(k=\left|\frac{d \alpha}{d s}\right|\)

由上述定义知，曲率是一个局部概念，谈曲线的弯曲应该具体地指出是曲线在哪一点处的弯曲，这样才准确。

曲率圆和曲率半径

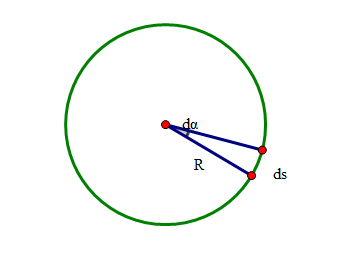
光滑曲线上某点的极小邻域，都可以看作是一个圆上的一部分，这个圆叫做曲率圆，这个圆的半径R叫做曲率半径。

如上图，在圆上\(\frac{d s}{R}=\tan d \alpha \approx d \alpha\) \(\Rightarrow R=\left|\frac{d s}{d \alpha}\right|\) 即\(k=\frac{1}{R}=\left|\frac{d \alpha}{d s}\right|\)

曲率的倒数就是曲率半径。

又$==y^{} $

$ ==y^{} $

$ =y^{} $

$d =y^{} ^{2} d x =y^{} d x $

又\(\mathrm{d} s=\sqrt{1+y^{\prime 2}} \mathrm{d} x,(\mathrm{d} x>0)\)

则可以得到曲率计算公式\(k=\frac{1}{R}=\left|\frac{d \alpha}{d s}\right| = \frac{\left|y^{\prime \prime}\right|}{\left[1+\left(y^{\prime}\right)^{2}\right]^{3 / 2}}\)

假设曲线方程是参数方程 \(\left\{\begin{array}{l}x=\varphi(t) \\ y=\phi(t)\end{array}\right.\) 给出

则(2)式可相应地改成形式：

\(y^{\prime}=\frac{\phi^{\prime}(t)}{\varphi^{\prime}(t)}\)，，\(y^{\prime \prime}=\frac{\phi^{\prime \prime}(t) \psi^{\prime}(t)-\varphi^{\prime \prime}(t) \phi^{\prime}(t)}{\left[\varphi^{\prime}(t)\right]^{3}}\)

可得参数方程曲率计算公式\(k=\frac{\left|\phi^{\prime \prime}(t) \varphi^{\prime}(t)-\varphi^{\prime \prime}(t) \phi^{\prime}(t)\right|}{\left[\left(\varphi^{\prime}(t)\right)^{2}+\left(\phi^{\prime}(t)\right)^{2}\right]^{3 / 2}}\)

例1