高等数学-一元积分学-不定积分

不定积分

概念与性质

原函数

原函数：如果\(F^{\prime}(x)=f(x)\)，则\(F(x)\)是\(f(x)\)的原函数。

如果\(f(x)\)存在原函数，则存在无穷多个原函数，且任意两个原函数相差常数。

原函数存在定理：连续函数一定存在原函数

不定积分

不定积分，即一个函数的原函数，包括它的所有原函数，即\(\int f(x) d x=F(x)+c\)

不定积分性质

以下在\(f(x)\)连续的前提下

\(\left(\int f(x) \mathrm{d} x\right)^{\prime}=f(x) ; \mathrm{d} \int f(x) \mathrm{d} x=f(x) \mathrm{d} x\)

\(\int f^{\prime}(x) \mathrm{d} x=f(x)+C_{;} \int \mathrm{d} f(x)=f(x)+C\)

\(\int(f(x) \pm g(x)) \mathrm{d} x=\int f(x) \mathrm{d} x \pm \int g(x) \mathrm{d} x\)

\(\int k f(x) \mathrm{d} x=k \int f(x) \mathrm{d} x,\) 常数 \(k \neq 0\)

不定积分工具

基本公式

\(\int k d x=k x+C\)

\(\int x^{a} d x=\left\{\begin{array}{ll} \frac{1}{a+1} \cdot x ^{a+1} & ,& a\neq -1\\ \ln |x|+c & , & a=-1\end{array}\right.\)

\(\int a^{x} d x=\frac{a^{x}}{\ln a}+c\)

\(\int e^{x} d x=e^{x}+c\)

\(\int \sin x d x=-\cos x+c\)

\(\int \cos x d x=\sin x+c\)

\(\int \tan x d x=-\ln |\cos x|+c\)

\(\int \cot x d x=\ln |\sin x|+c\)

\(\int \sec x d x=\ln |\sec x+\tan x|+c\)

\(\int \csc x d x=\ln |\csc x-\cot x|+c\)

\(\int \sec ^{2} x d x=\tan x+c\)

\(\int \csc ^{2} x d x=-\cot x+c\)

\(\int \sec x \tan x d x=\sec x+c\)

\(\int \csc x \cot x d x=-\csc x+c\)

平方和平方差公式

\(\int \frac{d x}{\sqrt{1-x^{2}}}=\arcsin x+c\)

\(\int \frac{d x}{\sqrt{a^{2}-x^{2}}}=\arcsin \frac{x}{a}+c\)

\(\int \frac{1}{1+x^{2}} d x=\arctan x+c\)

\(\int \frac{1}{a^{2}+x^{2}} d x=\frac{1}{a} \arctan \frac{x}{a}+c\)

\(\int \frac{1}{\sqrt{x^{2}+a^{2}}} d x=\ln (x+\sqrt{x^{2}+a^{2}})+c\)

\(\int \frac{1}{\sqrt{x^{2}-a^{2}}} d x=\ln |x+\sqrt{x^{2}-a^{2}}|+c\)

\(\int \frac{1}{x^{2}-a^{2}} d x=\frac{1}{2 a} \ln \left|\frac{x-a}{x+a}\right|+c\)

\(\int \sqrt{a^{2}-x^{2}} d x=\frac{a^{2}}{2} \arcsin \frac{x}{a}+\frac{1}{2} x \sqrt{a^{2}-x^{2}}+c\)

换元积分法

第一类换元积分法

如下面所示的换元积分过程，即为第一类换元积分法

\(\int f[\varphi(x)] \varphi^{\prime}(x) d x=\int f[\varphi(x)] d \varphi(a)\)

\(\overset{\varphi(x)=t}{=} \quad \int f(t) d t=F(t)+c=F[\varphi(x)]+c\)

第二类换元积分法

无理转有理（不一定需要）

• \(\int R(x, \sqrt[n]{a x+b}, \sqrt[m]{a x+b}) \mathrm{d} x\) 型 \(, a \neq 0\)。 命 \(\sqrt[mn]{a x+b}=t, x=\frac{t^{m n}-b}{a}, \mathrm{d} x=\frac{m n}{a} t^{m n-1} \mathrm{d} t\)
• \(\int R(x, \sqrt{\frac{a x+b}{c x+d}}) \mathrm{d} x\) 型 命 \(\sqrt{\frac{a x+b}{c x+d}}=t, x=\frac{d t^{2}-b}{a-c t^{2}}, \mathrm{d} x=\frac{2(a d-b c) t}{\left(a-c t^{2}\right)^{2}} \mathrm{d} t .\) 其中设 \(a d-b c \neq 0\)
• \(\int R(\sin x, \cos x) \mathrm{d} x\) 型 命 \(\tan \frac{x}{2}=t,\) 则 \(\sin x=\frac{2 t}{1+t^{2}}, \cos x=\frac{1-t^{2}}{1+t^{2}}, \mathrm{d} x=\frac{2}{1+t^{2}} \mathrm{d} t .\) 此称万能代换,非到不得己时不用.

平方和差的三角替换

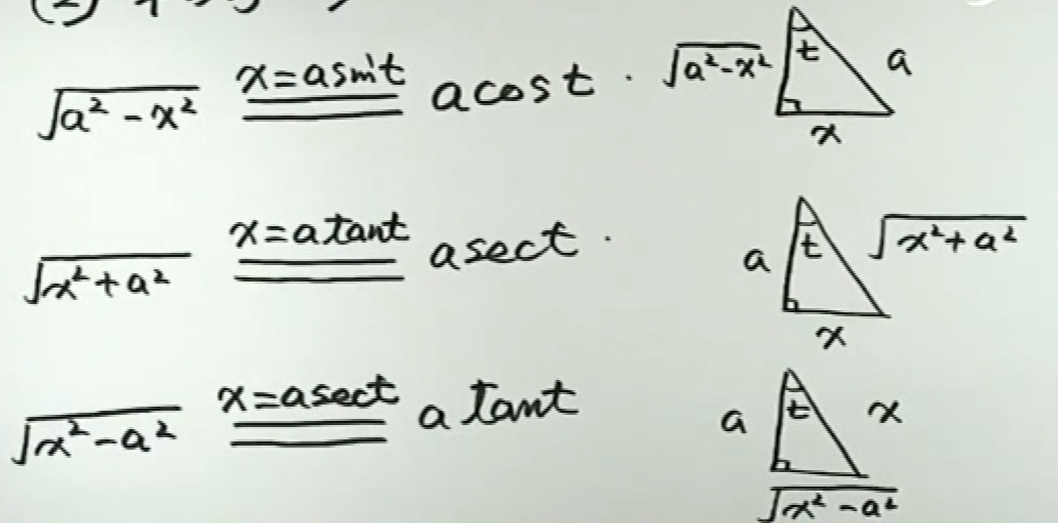
分部积分法

\((u v)^{\prime}=u^{\prime} v+u v^{\prime}\) \(u v=\int v d u+\int u d v\) \(\int u d v=u v-\int v d u\)

幂函数*指数函数的积分\(\int x^{n} \cdot e^{x} d x\)

幂函数*对数函数的积分\(\int x^{n} \cdot \ln x d x\)

幂函数*三角函数的积分\(\int x^{n} \cdot 三角函数 d x\)

幂函数*反三角函数的积分\(\int x^{n} \cdot 反三角函数 d x\)

指数函数*正余弦函数的积分\(\int e^{a x} \times\left\{\begin{array}{l}\cos b x \\ \sin b x\end{array} d x\right.\)

正余弦倒数的n次幂的积分（奇次幂）

特殊积分类型

有理分式\(\int R(x) d x\)的积分

其中\(R(x)=\frac{P(x)}{a(x)}\)，而P(x)和Q(x)为多项式

如果P的次数小于于Q的次数，称其为真分式； 如果P的次数大于等于Q的次数，称其为假分式

\(R(x)\)为假分式

如果\(R(x)\)为假分式，要先转换成： 多项式+真分式

例1

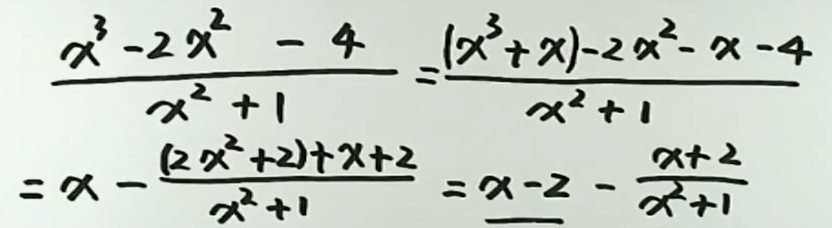
\(R(x)\)为真分式

如果\(R(x)\)为真分式，R(x)分子不变，分母因式分解；然后拆成部分和的形式。

例1

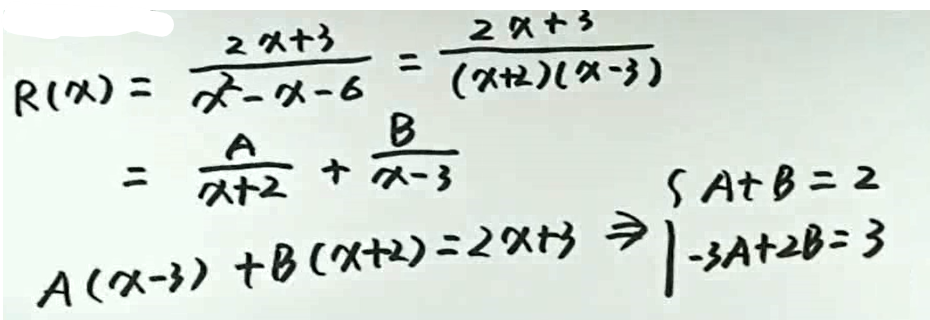
例2

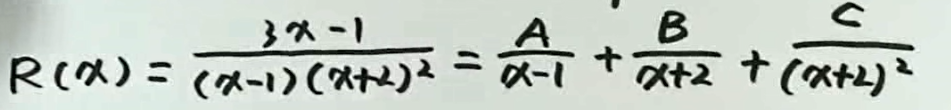
例3

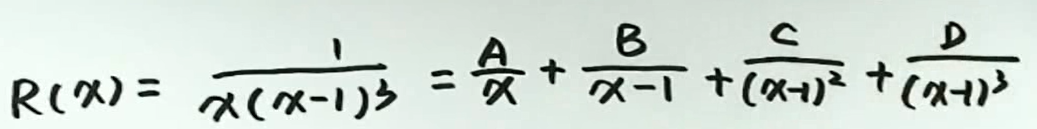
例4

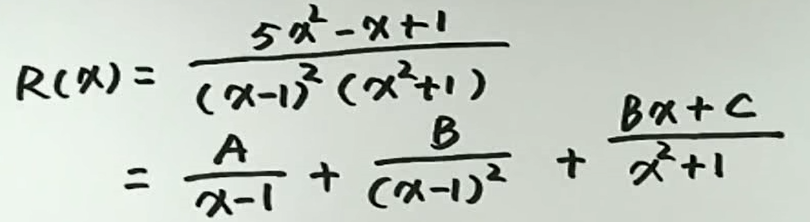
三角有理分式的积分

关于sinx,cosx的有理分式的积分，“万能代换”可解决这类间题。但随之而来的是一串复杂的计算，考研至今未见到过非要用它才能求这种不定积分的题对于这类题，

一般采用下列办法处理：①化成同角；②尽量约分；③分母化成单项式； ④利用\(1=\sin ^{2} x+\cos ^{2} x\)或\(1=\left(\sin ^{2} x+\cos ^{2} x\right)^{2}\)等等。由于三角公式众多，化简时有些技巧，考研中这类题出得很少，但也曾考过

简单无理分式的积分

按照几种典型类型换元法中所讲的方法换元

解路思路 含有\(\sqrt[n]{ax+b}, \sqrt[n]{ax+b}\)的简单分式的积分，一般命 \(\sqrt[k]{a x+b}=t(\text { 其中 } k \text { 为 } n, m\) 的最小公倍教）以去掉根式.

可以使用平方和三角替换的，画三角替换。

例1

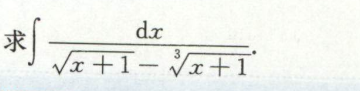
例2