高等数学-一元积分学-不定积分
高等数学-一元积分学-不定积分
求不定积分
换元积分法
第一类换元积分法
例1

例2
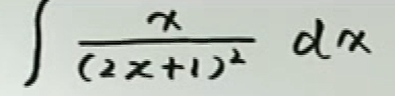

例3

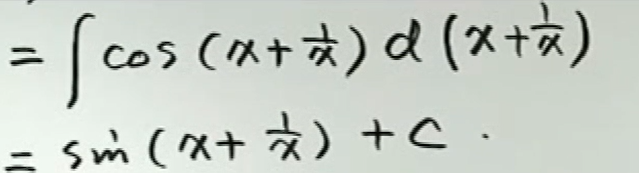
例4
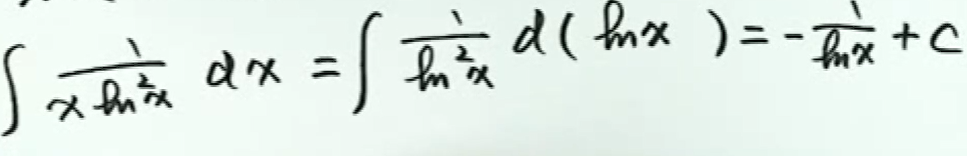
例5
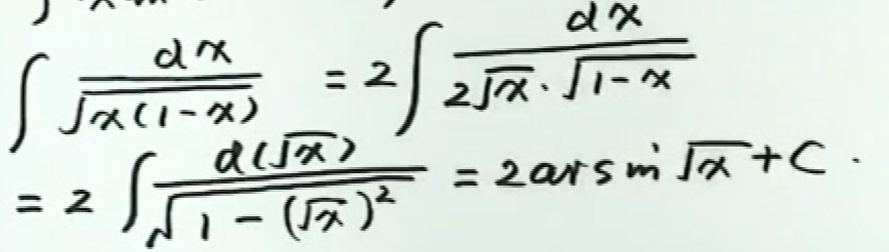
例6
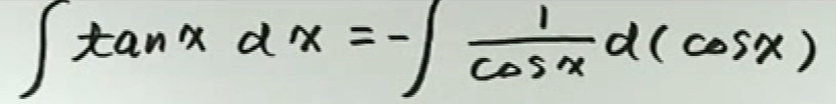

例7
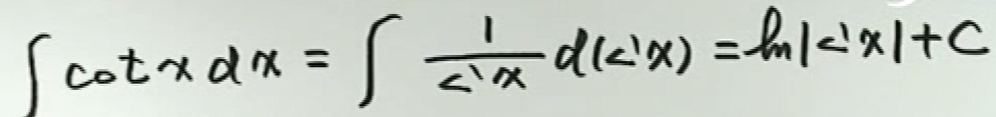
例8
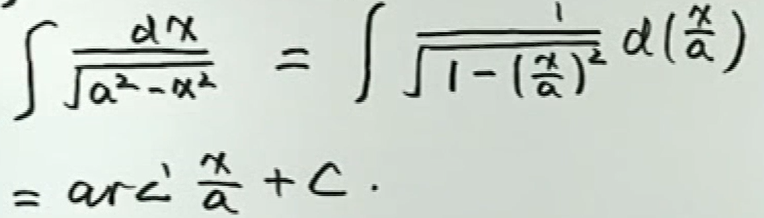
例9

例10

例11
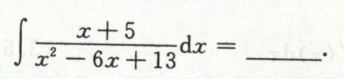

例12
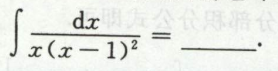

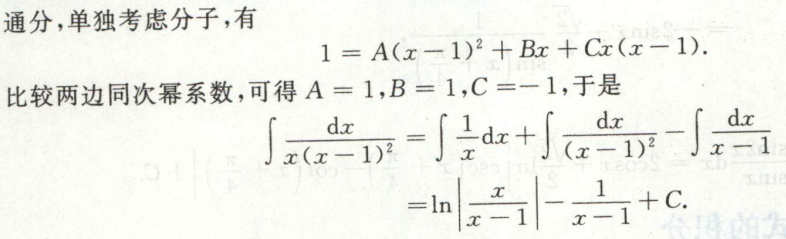

例13
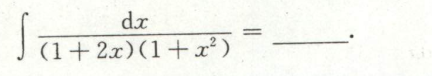
例14
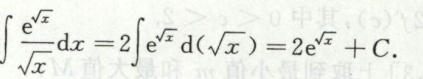
例15
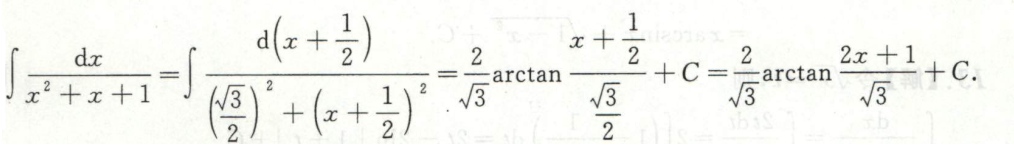
例16
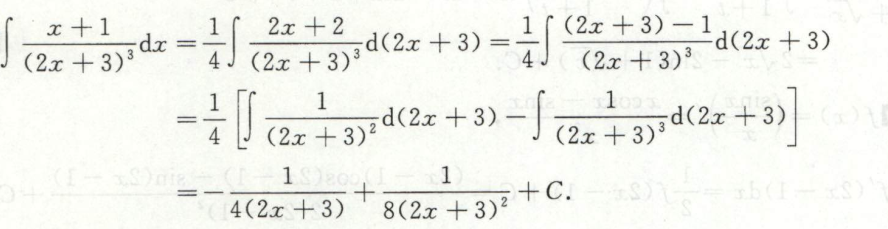
例17

例18

例19

例20

例21
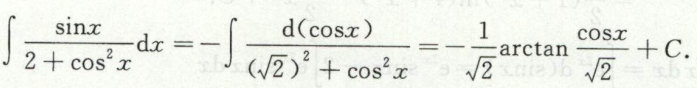
例22

例23

\(=-2\tan \frac{\sqrt{x}}{2} + C\)
此题后面中间也可以使用1的代换,三角半角公式来做
例24
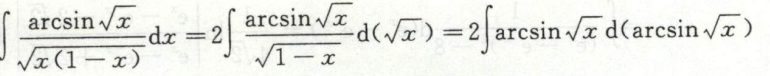
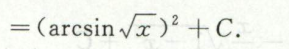
例25
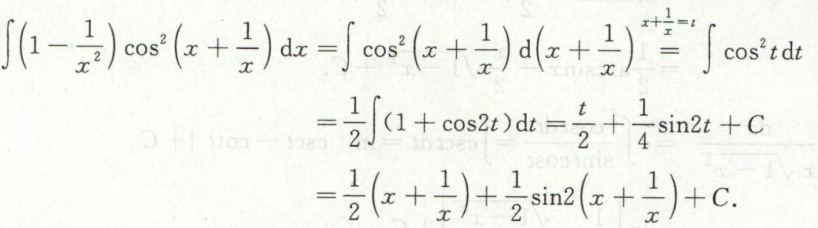
例26


例27
此题需要功底
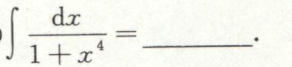

例28
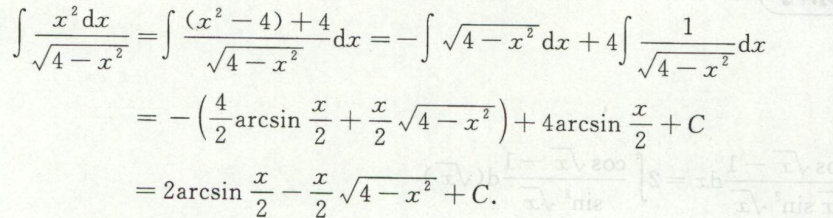
例29
此题需要功底

例30
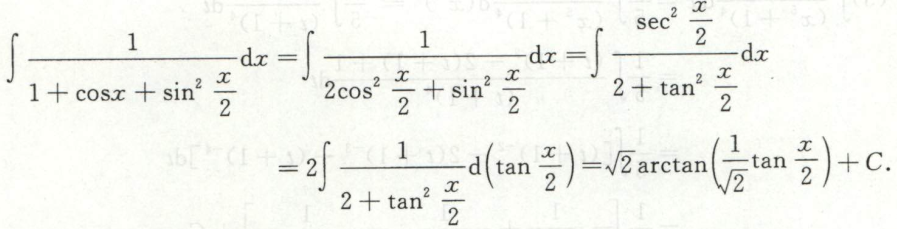
例31

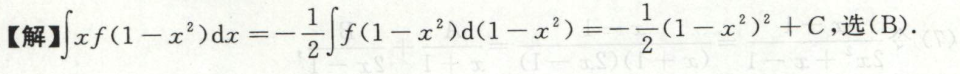
例32
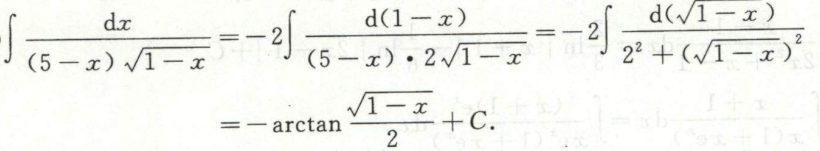
例33
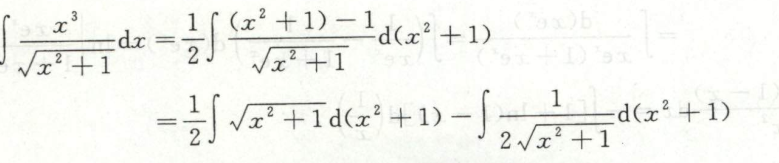
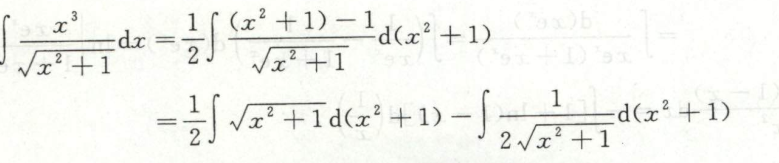
例34
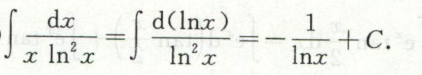
例35
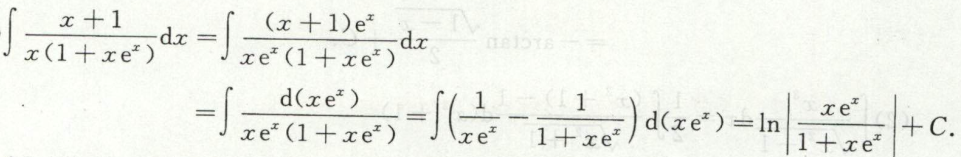
例36

例37
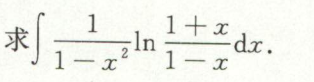
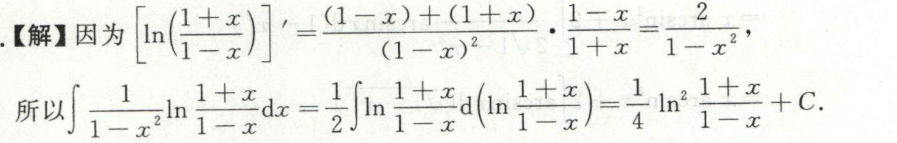
例38

例39

例40
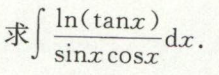

例41

例42

例43


例44
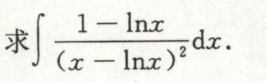

例45
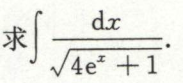
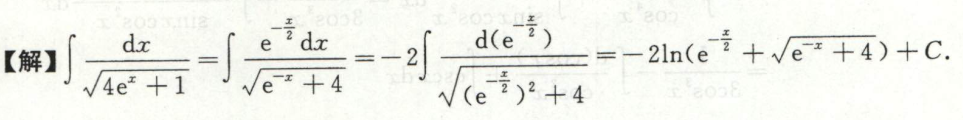
例46
第一换元积分,然后分部积分

例47
指数的这种变换要能想得到
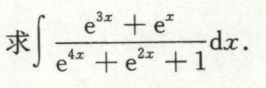
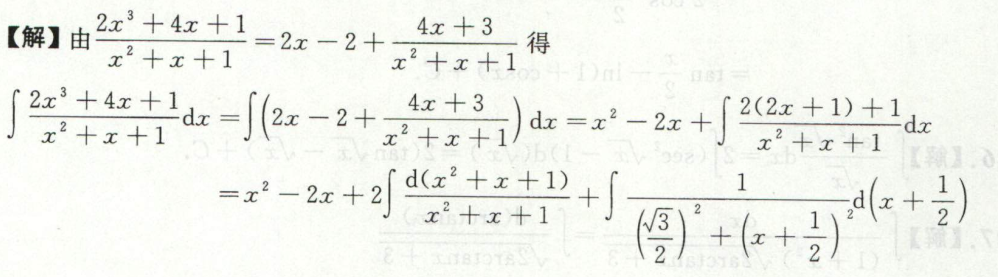
例48
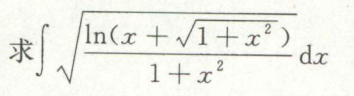

例49

例50
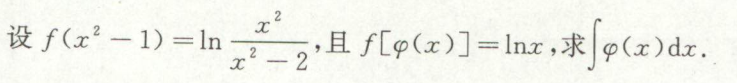
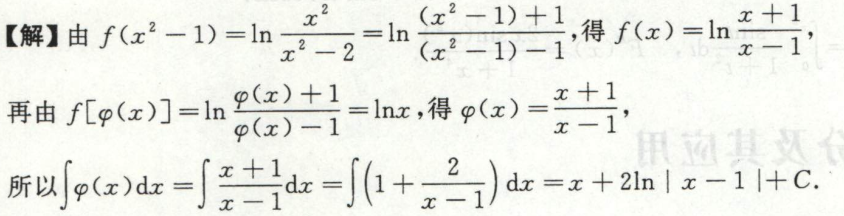
例51

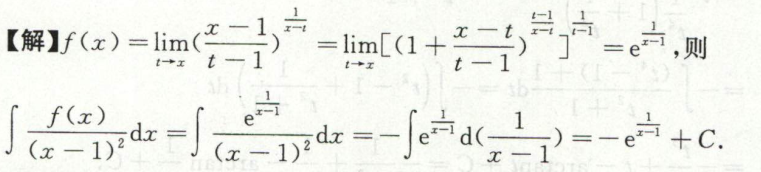
第二类换元积分法
无理转有理(不一定需要)
例1

例2
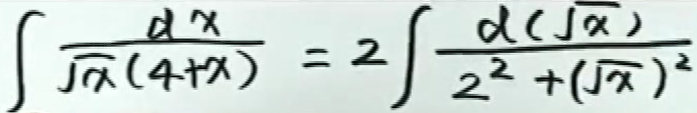
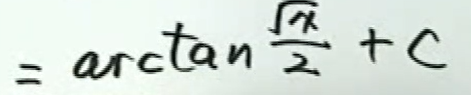
例3

例4
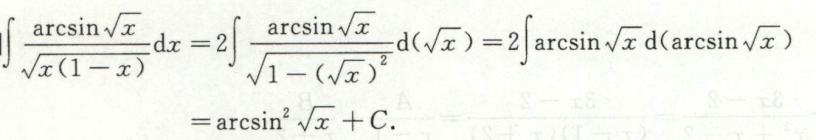
例5
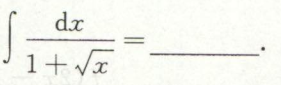
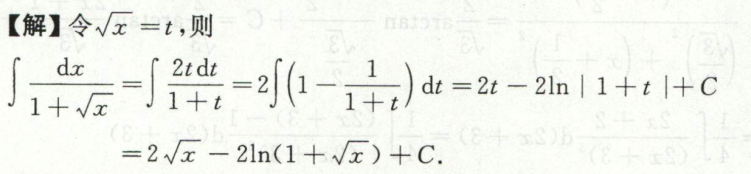
例6



例7

例8
第二换元积分,然后有理分式积分
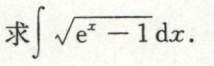

例9

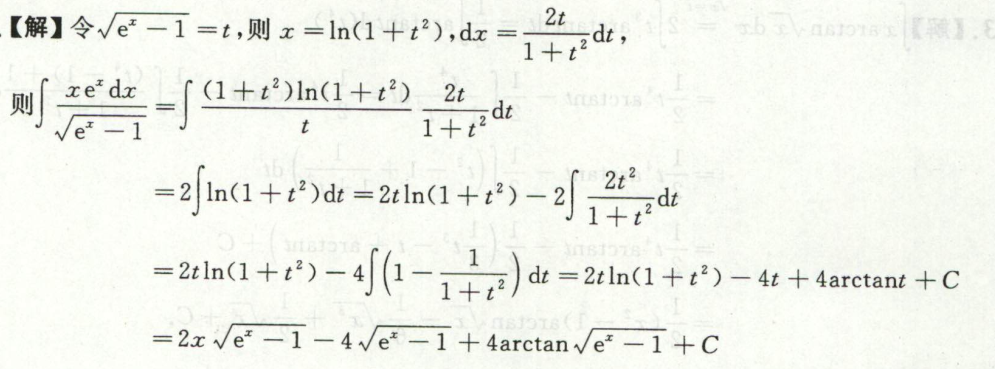
例10

平方和差转三角
例1

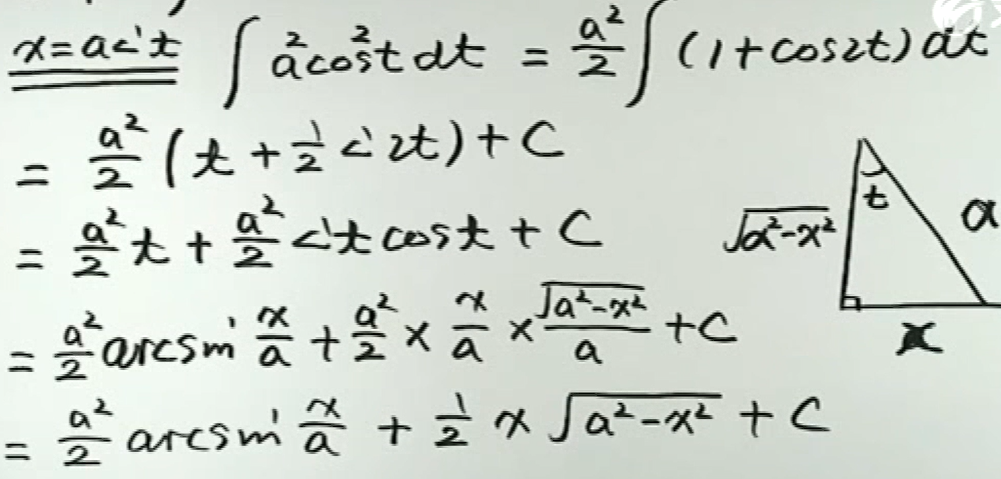
例2


例3


例4

例5

例6
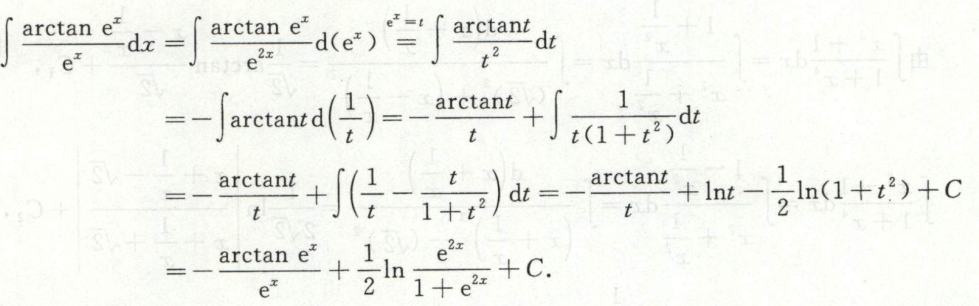
例7


例8
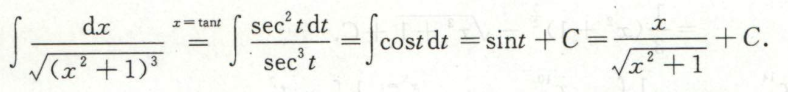
例9

例10
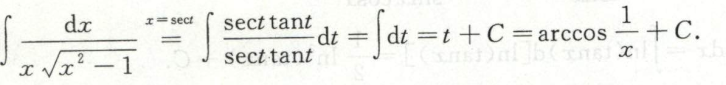
例11
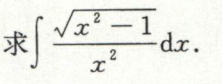

例12
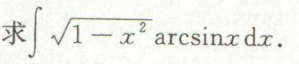

分部积分法
幂函数*指数函数的积分\(\int x^{n} \cdot e^{x} d x\)
例1


幂函数*对数函数的积分\(\int x^{n} \cdot \ln x d x\)
例1


例2
第一类换元积分+幂函数对数函数的积分

例3
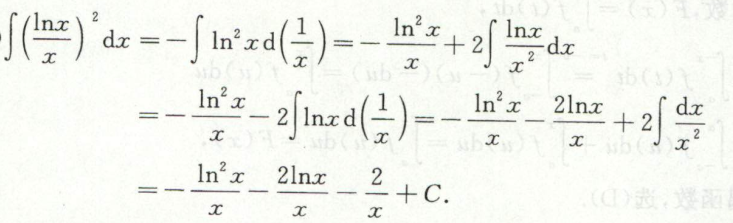
幂函数*三角函数的积分\(\int x^{n} \cdot 三角函数 d x\)
这里的三角函数,对于正弦余弦,要求变到1次幂;对于正切/余切/sec/csc,要求是2次方
例1


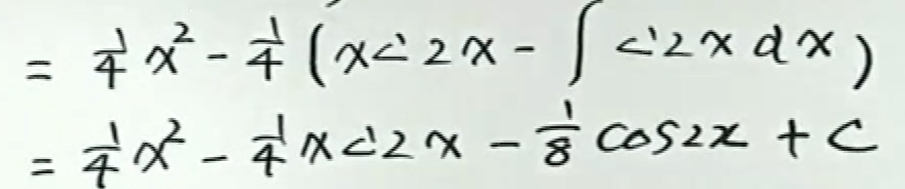
例2


例3
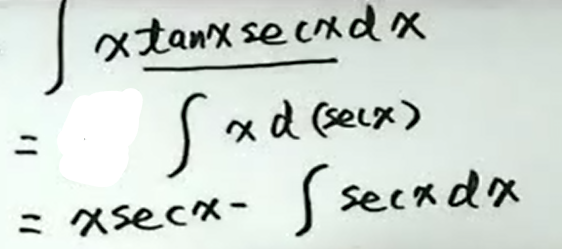
例4
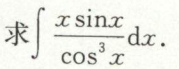

幂函数*反三角函数的积分\(\int x^{n} \cdot 反三角函数 d x\)
例1


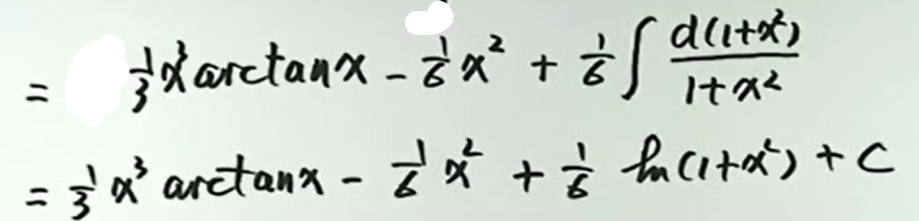
例2
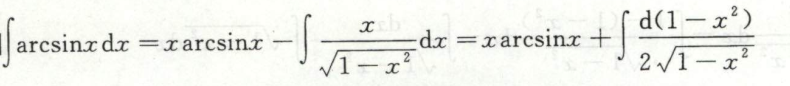

例3

例4
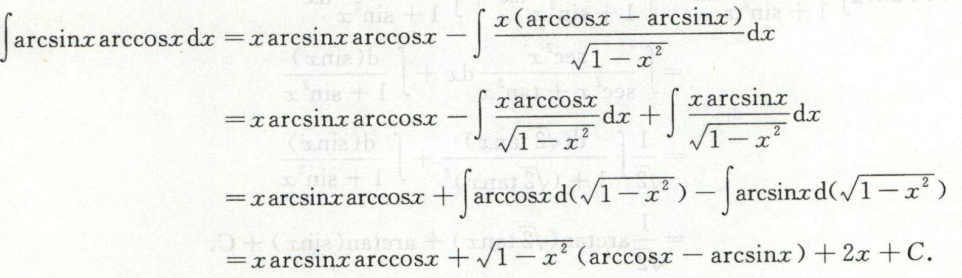
指数函数*正余弦函数的积分\(\int e^{a x} \times\left\{\begin{array}{l}\cos b x \\ \sin b x\end{array} d x\right.\)
例1
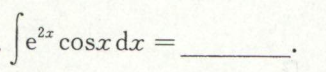

指数函数*反三角函数的积分
例1
指数函数*反三角函数,并与简单无理式复合。


sec或csc的n次幂的积分(奇次幂)
例1
sec或csc非奇数次幂的例子,直接计算

例2
非奇数次幂的例子,直接计算

例3


对数复合三角的积分
例1
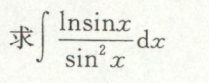

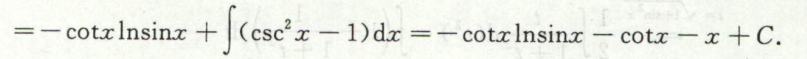
有理分式积分
有理分式\(\int R(x) d x\)的积分
其中\(R(x)=\frac{P(x)}{a(x)}\),而P(x)和Q(x)为多项式
如果P的次数小于于Q的次数,称其为真分式; 如果P的次数大于等于Q的次数,称其为假分式
为真分式
如果\(R(x)\)为真分式,R(x)分子不变,分母因式分解;然后拆成部分和的形式。
例1
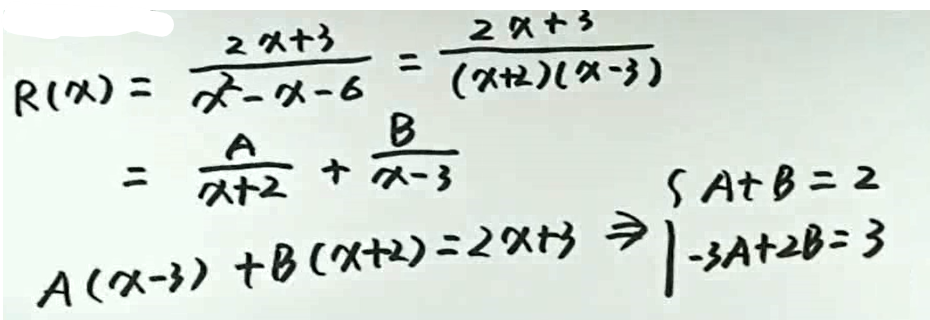
例2
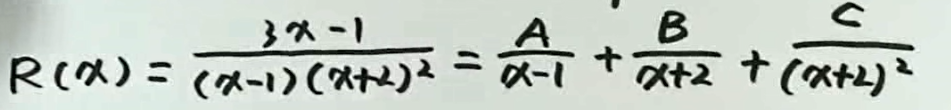
例3
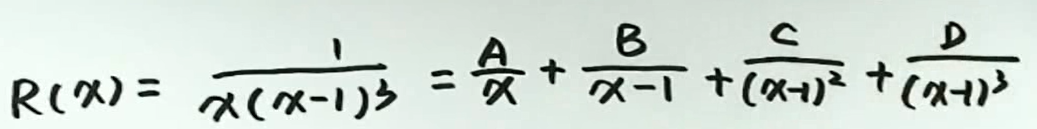
例4
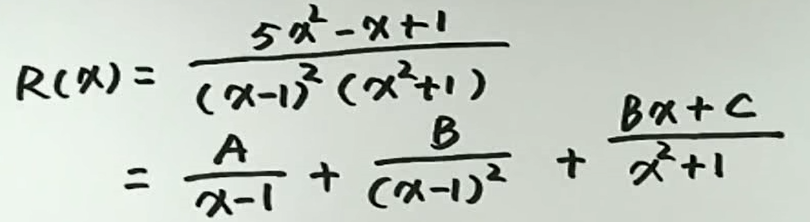
例5
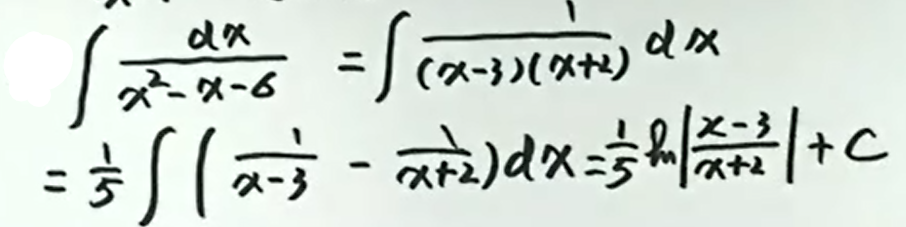
例6
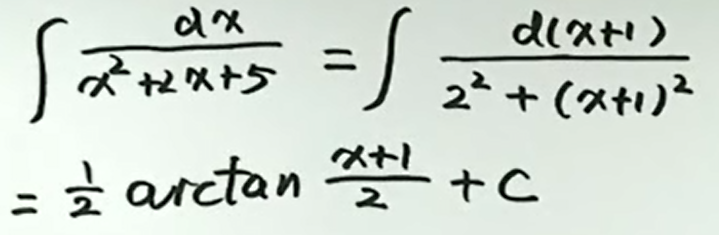
例7
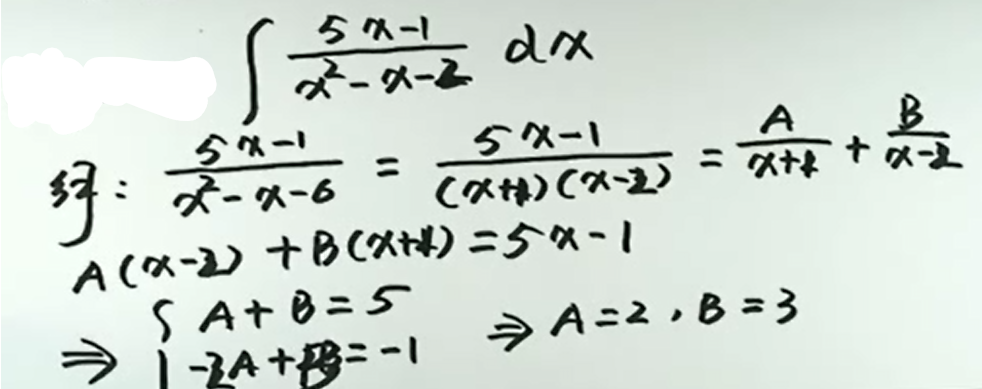

例8

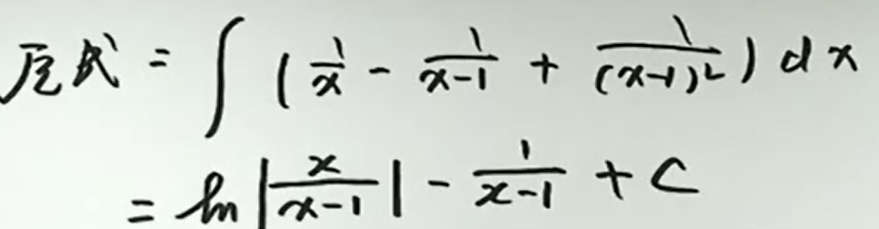
例9
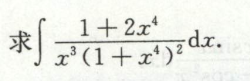

例10
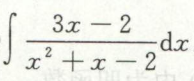

例11

例12


例13

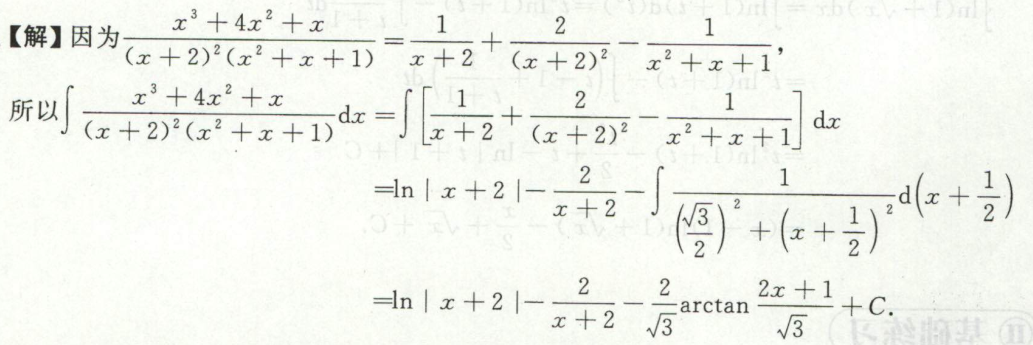
例14
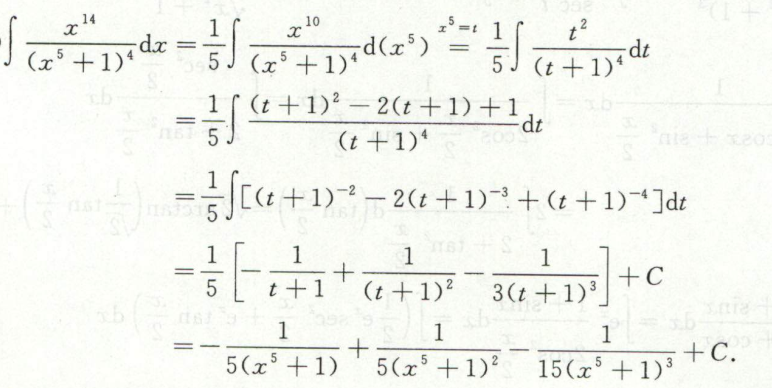
例15

例16


例17
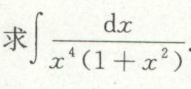

上面是换元法的答案,下面有理分式分解方法,没找到错在哪里
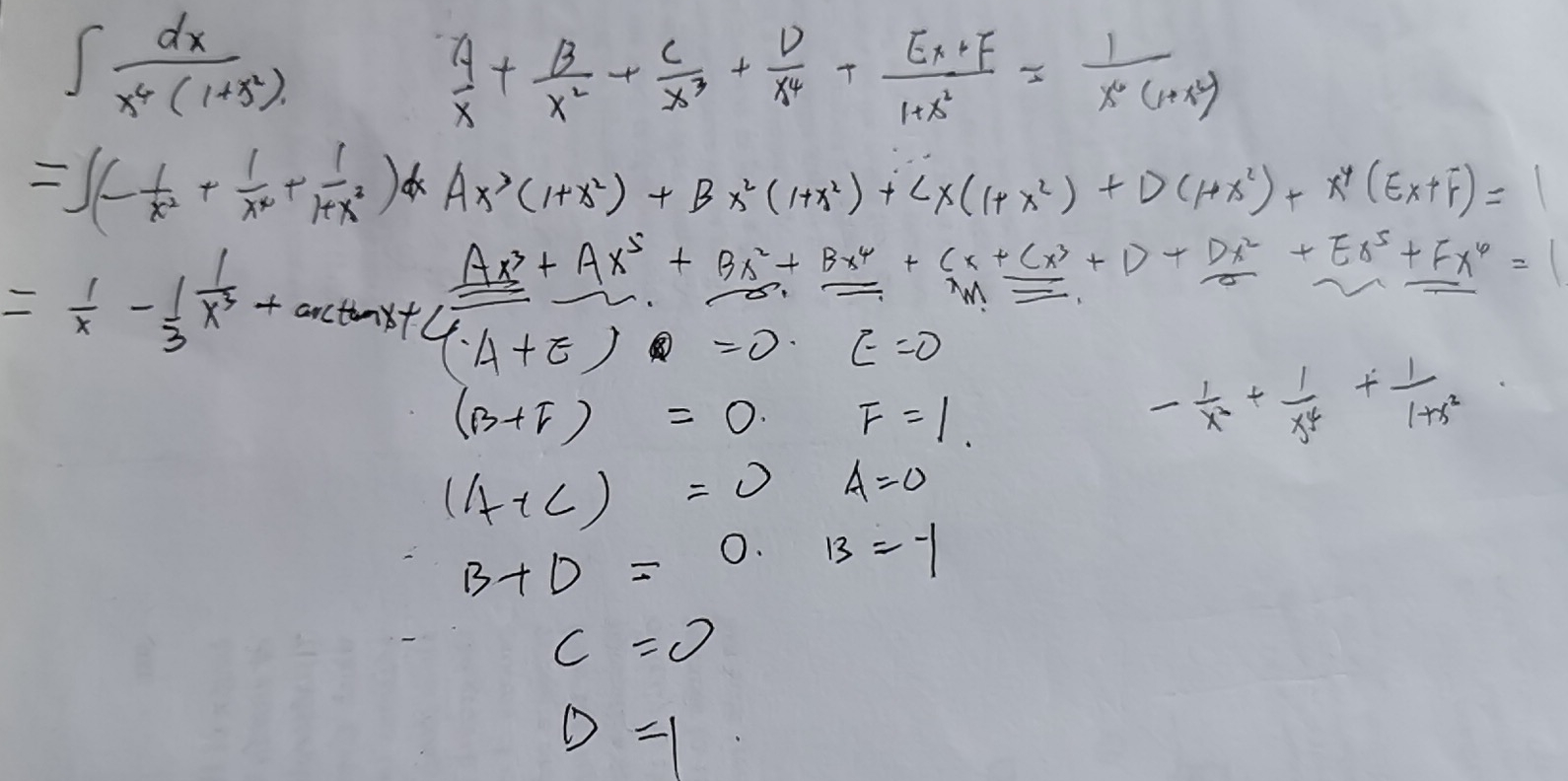
\(R(x)\)为假分式
如果\(R(x)\)为假分式,要先转换成: 多项式+真分式
例1
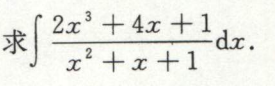

三角有理分式的积分
关于sinx,cosx的有理分式的积分,“万能代换”可解决这类间题。但随之而来的是一串复杂的计算,考研至今未见到过非要用它才能求这种不定积分的题对于这类题,一般采用下列办法处理:①化成同角;②尽量约分;③分母化成单项式; ④利用\(1=\sin ^{2} x+\cos ^{2} x\)或\(1=\left(\sin ^{2} x+\cos ^{2} x\right)^{2}\)等等。由于三角公式众多,化简时有些技巧,考研中这类题出得很少,但也曾考过
例1
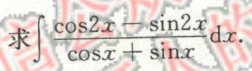
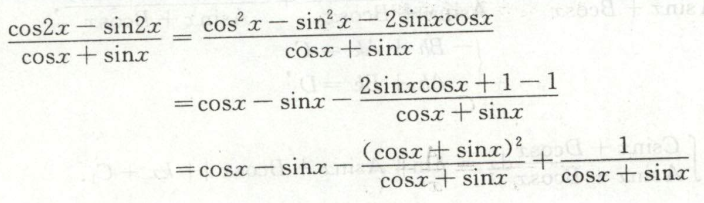

例2
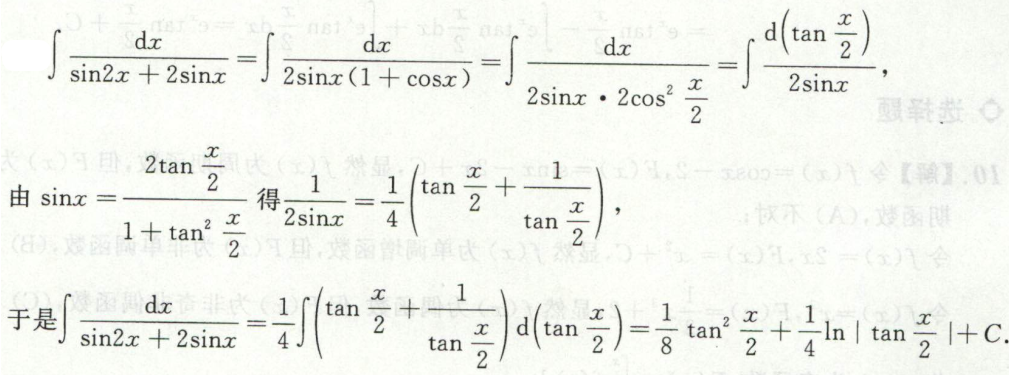
例3
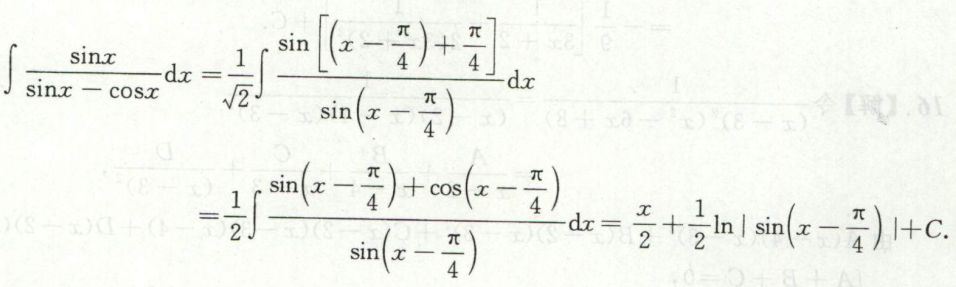
例4

例5

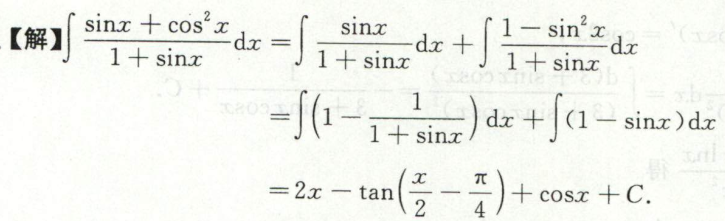
注:其中 \(\quad \int \frac{1}{1+\sin x} d x\) \(=\int \frac{1-\sin x}{1-\sin ^{2} x} d x\) \(=\int \frac{1}{\cos ^{2} x} d x-\int \frac{\sin x}{\cos ^{2} x} d x\) \(=\tan x+\int \frac{d \cos x}{\cos ^{2} x}\) \(=\tan x-\frac{1}{\cos x}+C\)
而结合万能公式和tan加法,又可化为\(\tan \left(\frac{x}{2}-\frac{\pi}{4}\right)+C\)
例6

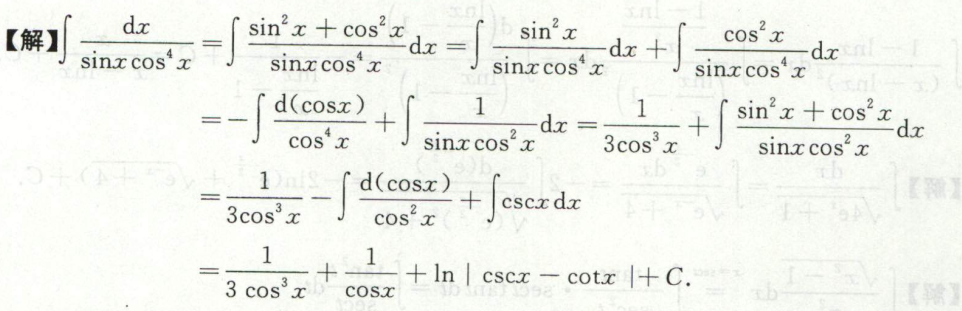
用万能公式解了一次,答案不一样,暂时找不到错误在哪里:

例7


例8
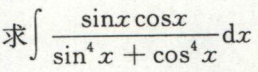

下面使用万能公式算了一遍,答案不一样,暂时找不到错在哪里:
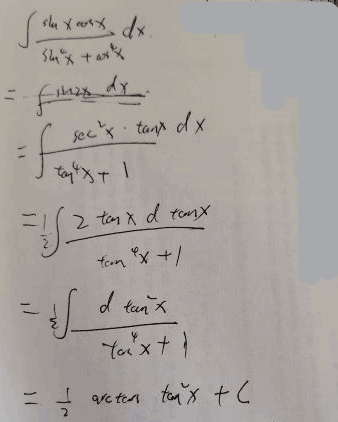
例9
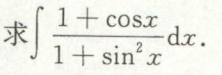

例10

例11

和上一题比较,注意体会这类题型的灵活性
换元+分部积分+有理分式
例1
第二换元积分,分部积分
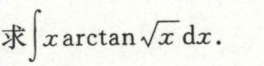

例2
第一换元积分,分部积分

例3


例4
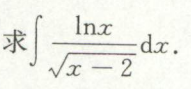
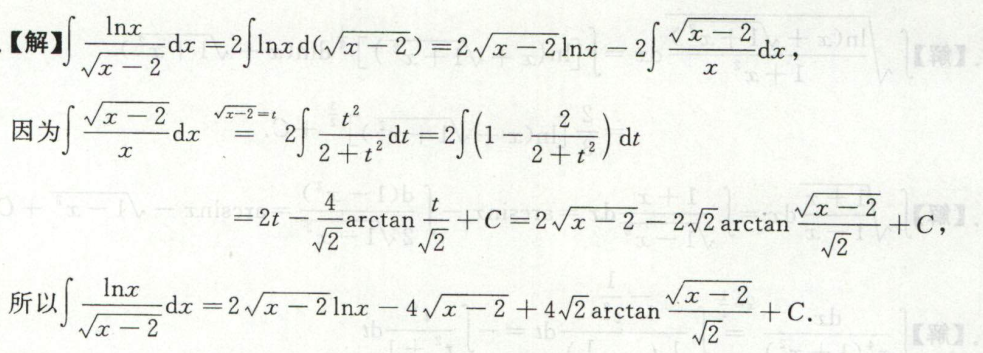
指数,有理分式,三角有理分式,简单无理式的混合或复合后的积分
例1
指数函数*反三角函数,并与简单无理式复合。


例2


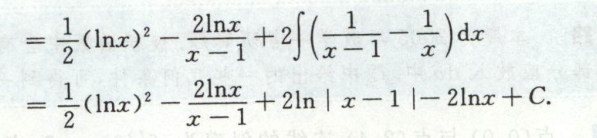
例3

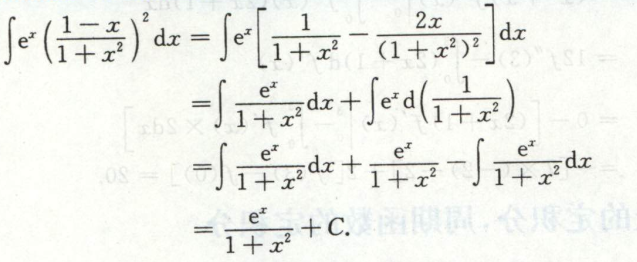
例4

例5
第一换元法+分部积分
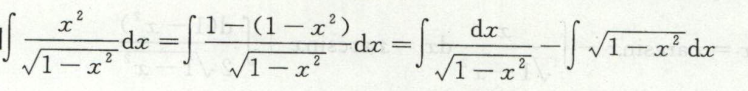
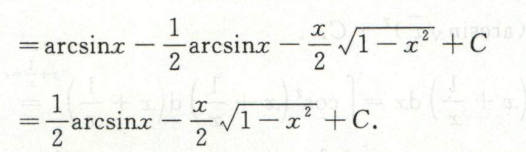
例6
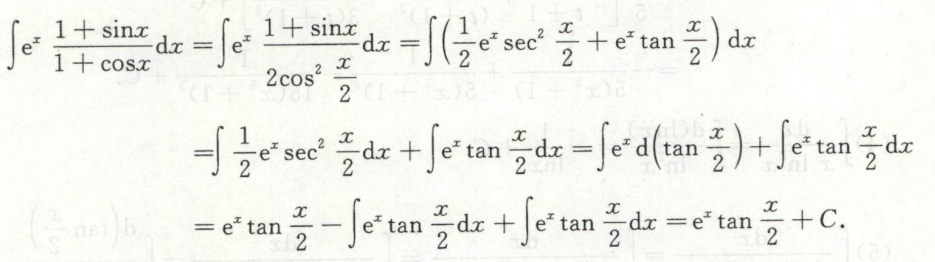
例7


例8



例9
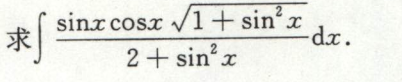


例10
三角有理分式和幂函数混合
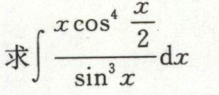

例11
无理式积分


求分段函数的不定积分
解题思路本题的被积函数为绝对值所表示,
第一步,应将它写成分段表达式,可知它是连续的; 第二步,将此分段函数按分段求其原函数,并使在分界点处接成连续,
再加C便可得不定积分
例1
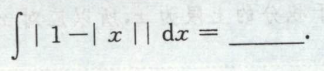

例2

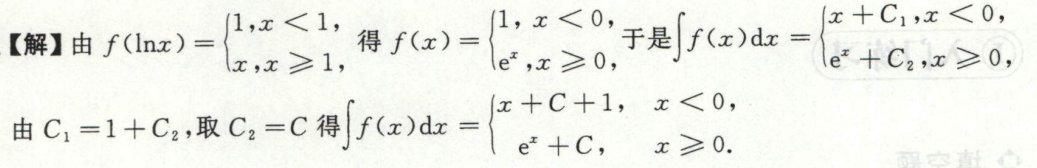
求带导数或带积分的不定积分
例1


比较不定积分的大小
例1

