高等数学-一元积分学-定积分与反常积分
高等数学-一元积分学-定积分与反常积分
定积分
定积分概念
函数\(f(x)\)在[a,b]有定义且有界,分割为\(\Delta x_i\)小段,每段上取点\(\xi_i\)处函数值作乘积\(f\left(\xi_{i}\right) \Delta x_{i}\),求和取极限\(\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}\right) \Delta x_{i}\),其中\(\lambda=\max _{1 \leq i \leq n}\left|\Delta x_{i}\right|\)
如果上述极限存在,则称\(f(x)\)在[a,b]上可积,并称上述极限为\(f(x)\)在[a,b]上的定积分,记为\(\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}\right) \Delta x_{i}=\int_{a}^{b} f(x) \mathrm{d} x\)
(有界是可积的必要条件)
定积分和原函数存在的判定
定积分存在定理
\(f(x)\)在[a,b]上连续,则定积分\(\int_{a}^{b} f(x) \mathrm{d} x\)存在
\(f(x)\)在[a,b]上有界,且只有有限个间断点,则定积分\(\int_{a}^{b} f(x) \mathrm{d} x\)存在(一般可以看作多个连续的定积分相加)
原函数存在定理
\(f(x)\)在[a,b]上连续,则原函数存在
注:如果\(f(x)\)不连续,则原函数存在与否与定积分\(\int_{a}^{b} f(x) \mathrm{d} x\)存在与否不相关
牛顿-莱布尼兹定理
由前面定理\(f(x)\)在[a,b]上连续,则原函数存在,定积分存在。
若\(f(x)\)在[a,b]上连续,\(F(x)\)是\(f(x)\)的一个原函数,则\(\int_{a}^{b} f(x) \mathrm{d} x=\left.F(x)\right|_{a} ^{b}=F(b)-F(a)\),这个关系叫做牛顿-莱布尼兹公式
证明:
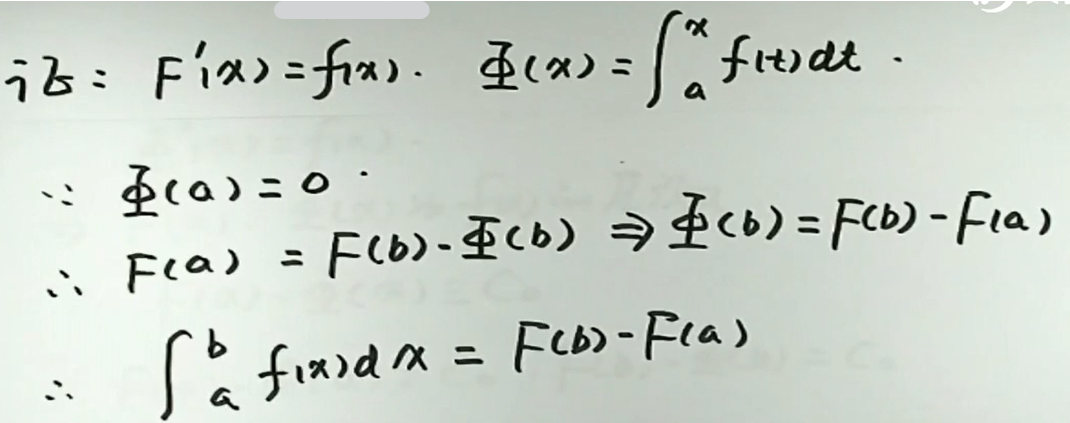
定积分性质
以下均设\(f(x)\)与\(g(x)\)可积
四则与上下限
\(\int_{a}^{b} f(x) \mathrm{d} x=-\int_{b}^{a} f(x) \mathrm{d} x\)
\(\int_{a}^{a} f(x) \mathrm{d} x=0\)
\(\int_{a}^{b}[f(x) \pm g(x)] \mathrm{d} x=\int_{a}^{b} f(x) \mathrm{d} x \pm \int_{a}^{b} g(x) \mathrm{d} x\)
\(\int_{a}^{b} k f(x) \mathrm{d} x=k \int_{a}^{b} f(x) \mathrm{d} x, k\) 为常数
\(\int_{a}^{b} f(x) \mathrm{d} x=\int_{a}^{c} f(x) \mathrm{d} x+\int_{c}^{b} f(x) \mathrm{d} x\)
一些特殊上下限变换:
\(\int_{-a}^{0} \overset {x=-t}{=} \int_{0}^{a}\) , 如:\(\int_{-a}^{0} f(x) d x=\int_{0}^{a} f(-x) d x\)
\(\int_{a}^{b} \overset{x+t=a+b}{=} \int_{a}^{b}\) ,如: \(\int_{a}^{b} f(x) d x=\int_{a}^{b} f(a+b-x) d x\)
\(\int_{a}^{a+T} \overset{x-a=t}{=} \int_{0}^{T}\)
\(\int_{a}^{b} \overset {x=a+(b-a) t}{=} \int_{0}^{1}\)
缩放
\(f(x) \leqslant g(x), a \leqslant b,\) 则 \(\int_{a}^{b} f(x) \mathrm{d} x \leqslant \int_{a}^{b} g(x) \mathrm{d} x\)
若 \(f(x) \text { 与 } g(x) \text { 在区间[ } a, b]\) 上连续, \(f(x) \leqslant g(x)\),且至少存在点 \(x_{1}, a \leqslant x_{1} \leqslant b\),使 \(f\left(x_{1}\right)<g\left(x_{1}\right),\) 则\(\int_{a}^{b} f(x) \mathrm{d} x<\int_{a}^{b} g(x) \mathrm{d} x\)
\(\left|\int_{a}^{b} f(x) d x\right| \leqslant \int_{a}^{b} | f(x) | d x \quad(a<b)\)
积分中值定理
设 \(f(x) \text { 在[ } a, b]\) 连续,则至少存在一点 \(\xi \in [a, b]\) 使\(\int_{a}^{b} f(x) d x=f(\xi)(b-a)\)
证明:(用介值定理证明)
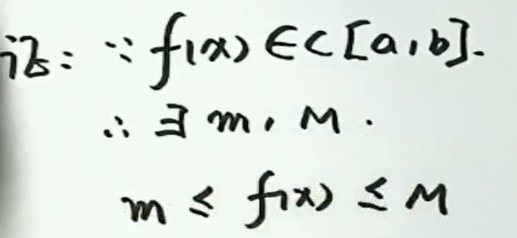
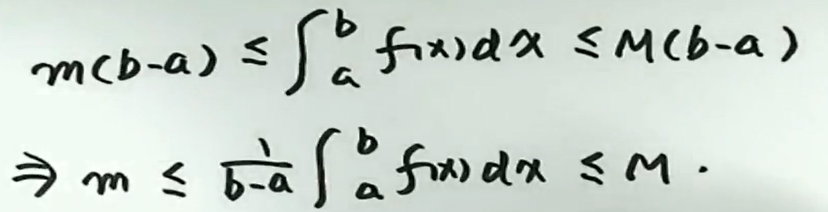

对称奇偶周期性
设 \(f(x) \text { 在[ }-a, a](a>0)\) 上是个连续函数,则\(\int_{-a}^{a} f(x) d x=\int_{0}^{a}[f(x)+f(-x)] d x\)
设 \(f(x) \text { 在[ }-a, a](a>0)\) 上是个连续的偶函数,则\(\int_{-a}^{a} f(x) \mathrm{d} x=2 \int_{0}^{a} f(x) \mathrm{d} x\)
设 \(f(x) \text { 在[ }-a, a](a>0)\) 上是个连续的奇函数,则 \(\int_{-a}^{a} f(x) \mathrm{d} x=0\)
设 \(f(x) \text { 在(一 } \infty,+\infty)\) 内是以 \(T\) 为周期的连续函数,则对于任意的常数 \(a,\) 恒有\(\int_{a}^{a+T} f(x) \mathrm{d} x=\int_{0}^{T} f(x) \mathrm{d} x\)
设 \(f(x) \text { 在(一 } \infty,+\infty)\) 内是以 \(T\) 为周期的连续函数,则\(\int_{0}^{n T} f(x) d x=n \int_{0}^{T} f\left(x\right) d x\)
\(\int_{0}^{\frac{\pi}{2}} f(\sin x) d x=\int_{0}^{\frac{\pi}{2}} f(\cos x) d x\)
华里士公式:\(I_n = \int_{0}^{\frac{\pi}{2}} \sin ^{n} x \mathrm{d} x=\int_{0}^{\frac{\pi}{2}} \cos ^{n} x \mathrm{d} x=\left\{\begin{array}{lr}\frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdot \cdots \cdot \frac{1}{2} \cdot \frac{\pi}{2}, & \text { 当 } n \text { 为正偶数 } \\ \frac{n-1}{n} \cdot \frac{n-3}{n-2} \cdots \cdots \frac{2}{3} \cdot 1, & \text { 当 } n \text { 为大于 } 1 \text { 的正奇数. }\end{array}\right.\) 即\(\left\{ \begin{aligned} & I_{n}=\frac{n-1}{n} I_{n-2} \\ & I_{0}=\frac{\pi}{2} \\ & I_{1}=1 \end{aligned}\right.\)
\(\int_{0}^{\pi} f\left(\sin x\right) d x=2 \int_{0}^{\frac{\pi}{2}} f\left(\sin x\right) d x\)
\(\int_{0}^{\pi} f(|\cos x|) d x=2 \int_{0}^{\frac{\pi}{2}} f(\cos x) d x\)
一个比较常用的变换公式:
\(\int_{0}^{\pi} x f(\sin x) d x=\frac{\pi}{2} \int_{0}^{\pi} f(\sin x) d x=\pi \int_{0}^{\frac{x}{2}} f(\sin x) d x\)
证明:
定积分积分法
定积分的换元积分法
定积分换元积分时,和不定积分的区别在于:换元时,积分上、下限应跟着换,而不必像不定积分那样求出原函数后代回成原变量x.
定积分的分部积分法
\(\int_{a}^{b} u(x) v^{\prime}(x) \mathrm{d} x=\left.u(x) v(x)\right|_{a} ^{b}-\int_{a}^{b} v(x) u^{\prime}(x) \mathrm{d} x\) 或\(\int_{a}^{b} u(x) \mathrm{d} v(x)=\left.u(x) v(x)\right|_{a} ^{b} - \int_{a}^{b} v(x) \mathrm{d} u(x)\) 相对不定积分,只是多了积分上下限。
变限积分函数
积分上限函数
\(\int_{a}^{x} f(t) d t \triangleq \Phi(x)\)
积分下限函数
类似积分上限函数定义
上限积分函数求导
\(f(x)\)在[a,b]上连续,$ (x)={a}^{x} f(t) d t \(,则\)^{}(x)=({a}^{x} f(t) t)x^{} =f(x), x \(,即\){a}^{x} f(t) t\(是\)f(x)$的一个原函数
推论:\(\frac{d}{d x} \int_{a}^{\varphi(x)} f(t) d t=f[\varphi(x)] \cdot \varphi^{\prime}(x)\)
推论:\(\frac{d}{d x} \int_{\varphi_1(x)}^{\varphi_2(x)} f(t) d t=f\left[\varphi_{2}(x)\right] \varphi_{2}^{\prime}(x)-f\left[\varphi_1 (x)\right] \varphi_{1}^{\prime}(x)\)
反常积分(广义积分)
正常积分
积分区间有限 \(f(x)\)在区间[a,b]上连续,或存在有限个第一类间断点
定义域无限的反常积分
$_{a}^{+} f(x) d x $型
\(f(x)\)在\([a,+\infty)\)连续,求$_{a}^{+} f(x) d x $
正常积分有牛顿-莱布尼兹公式\(\int_{a}^{b} f (x) d x=F(b)-F(a)\)
\(F(b)-F(a)\)与\(\int_{a}^{+\infty} f(x) d x\)不同,但是当\(b \rightarrow +\infty\),则相同.
计算
可以根据定义来计算\(\int_{a}^{+\infty} f(x) d x =\lim _{b \rightarrow+\infty} \int_{a}^{b} f(x) \mathrm{d} x = \lim_{b \rightarrow +\infty}[F(b)-F(a)] = \left\{\begin{array}{l} =A \text { ,收敛 }\\ \text { 不存在,发散 } \end{array} \right.\)
也可以判敛之后,根据正常积分的步骤来计算。
判敛
比较审敛法
极限审敛法:若\(\lim_{n \rightarrow \infty} x^{\alpha} \cdot f(x)=c_{0}(\neq 0)\),则\(\left\{\begin{aligned}\text{收敛},\alpha >1 \\ \text{发散}, \alpha \le 1\end{aligned}\right.\)
$_{-}^{a} f(x) d x $型
\(f(x)\)在\([-\infty,a)\)连续,求$_{-}^{a} f(x) d x $
判敛和计算方式与趋于正无穷的反常积分类似.
$_{-}^{+} f(x) d x $型
\(f(x)\)在\([a,+\infty)\)连续,求$_{-}^{+} f(x) d x $
判敛:
${-}^{+} f(x) d x \(收敛\)$ ${-}^{a} f(x) d x \(与\)_{a}^{+} f(x) d x $都收敛
注意:要想对该类广义积分使用定积分对称区间上的性质,前提是该广义积分收敛.
函数值域无界的反常积分
端点处\(f(a+) \rightarrow \infty\)的 \(\int_{a}^{b} f (x) d x\)型
\(f(x)\)在\((a,b]\)连续,求\(\int_{a}^{b} f (x) d x\)
根据牛顿-莱布尼兹公式有\(\forall \varepsilon>0 , \int_{a+\varepsilon}^{b} f(x) d x=F(b)-F(a+\varepsilon)\)
\(F(b)-F(a+\varepsilon)\)与\(\int_{a}^{b} f (x) d x\)不等,但是\(\varepsilon \rightarrow 0\)则相同
计算
可以根据定义计算\(\int_{a}^{b} f (x) d x =\lim _{a \rightarrow a+} \int_{a}^{b} f(x) d x= \lim_{\varepsilon \rightarrow 0} \left[ F(b)-F(a+\varepsilon) \right] = \left\{\begin{array}{l} =A \text { ,收敛 }\\ \text { 不存在,发散 } \end{array} \right.\)
也可以判敛之后按正常积分来计算
判敛
比较审敛法
极限审敛法:\(\lim_{x \rightarrow a^{+}}(x-a)^{\alpha} \cdot f(x)=C\).则\(\left\{\begin{aligned}\text{收敛},\alpha <1 \\ \text{发散}, \alpha \ge 1\end{aligned}\right.\)
端点处\(f(b-) \rightarrow \infty\)的 \(\int_{a}^{b} f (x) d x\)型
\(f(x)\)在\([a,b)\)连续,求\(\int_{a}^{b} f (x) d x\)
计算与判敛类似左端点函数值趋于无穷的情况
端点处\(f(a+) \rightarrow \infty\)且\(f(b-) \rightarrow \infty\)的 \(\int_{a}^{b} f (x) d x\)型
\(f(x)\)在\((a,b)\)连续,求\(\int_{a}^{b} f (x) d x\)
计算与判敛同上,判敛要对两个端点都进行一次
区间中有\(f(c) \rightarrow \infty\)的 \(\int_{a}^{b} f (x) d x\)型
\(f(x)\)在\([a, c) \cup(c, b]\)连续,且\(\lim_{x \rightarrow c} f(x) = \infty\),求\(\int_{a}^{b} f (x) d x\)
${a}^{b} f(x) d x \(收敛\)$ ${a}^{c} f(x) d x \(与\)_{c}^{b} f(x) d x $都收敛
反常积分的审敛
反常积分的审敛
不通过被积函数的原函数判定反常积分收敛性的判定方法
反常积分审敛依据的定理
定理 1(单调有界必收敛)
设函数 \(f(x)\) 在区间 \([a,+\infty)\) 上连续且 \(f(x) \geq 0 . \quad\) 若函数 \(F(x)=\int_{a}^{x} f(t) d t\)在\([a,+\infty)\) 上有上界,则反常积分 \(\int_{a}^{+\infty} f(x) d x\) 收敛.
定理2(比较审敛原理)
设函数 \(f(x), g(x)\) 在区间 \([a,+\infty)\) 上连续、非负,如果 \(f(x) \leq g(x),(a \leq x<+\infty),\) 并且 \(\int_{a}^{+\infty} g(x) d x\) 收敛,则 \(\int_{a}^{+\infty} f(x) d x\) 也收敛 \(; \quad\) 如果 \(f(x) \geq g(x),(a \leq x<+\infty)\)并且 \(\int_{a}^{+\infty} g(x) d x\) 发散,则 \(\int_{a}^{+\infty} f(x) d x\) 也发散.(可依据定理1推导)
区间 \((-\infty,a]\) 上连续, 或者 \(f(x) \leq 0 \quad\)情况类似.
无穷限反常积分的审敛法
特别地,取 \(g(x)=\frac{1}{x^{p}}\),就可由定理2(比较审敛原理)推出下面的定理3(比较审敛法)
定理3(比较审敛法 1)
设函数 \(f(x)\) 在区间 \([a,+\infty) \quad(a>0)\) 上连续,且 \(f(x) \geq 0\) . 如果存在常数 M >0 及 p>1,使得 \(\left.f(x) \leq \frac{M}{x^{p}},(a \leq x<+\infty), \text { 则 }\right] \int_{a}^{+\infty} f(x) d x\) 收敛; 如果存在常数 N > 0,使得 \(f(x) \geq \frac{N}{x}(a \leq x<+\infty),\) 则 \(\int_{a}^{+\infty} f(x) d x\) 发散.
定理4(极限审敛法 1)
比较审敛法,移项取极限可得如下极限审敛法:
设函数 \(f(x)\) 在区间 \([a,+\infty)(a>0)\) 上连续,且 \(f(x) \geq 0\) 。如果存在常数 \(p>1,\) 使得 \(\lim _{x \rightarrow+\infty} x^{p} f(x)\) 存在 则\(\int_{a }^{+\infty} f(x) d x\)收敛: 如果 \(\lim _{x \rightarrow+\infty} x f(x)=d>0\left(\text { 或 } \lim _{x \rightarrow+\infty} x f(x)=+\infty\right),\) 则\(\int_{a}^{+\infty} f(x) d x\) 发散.
定理5(积分的绝对值小于绝对值的积分)
设函数 \(f(x)\) 在区间 \([a,+\infty)\) 上连续, 如果 \(\int_{a}^{+\infty}|f(x)| d x\) 收敛,则 \(\int_{a}^{+\infty} f(x) d x\) 也收敛,称其绝对收敛.
无界函数反常积分的审敛法
定理6(比较审敛法2)
设函数 \(f(x)\) 在区间 \((a, b]\) 上连续,且 \(f(x) \geq 0\) ,\(x=a\) 是瑕点.如果存在常数 \(M>0\) 及 \(q<1\) 使得 \(\quad f(x) \leq \frac{M}{(x-a)^{q}} \quad(a<x \leq b)\) 则反常积分 \(\int_{a}^{b} f(\boldsymbol{x}) d x\) 收敛; 如果存在常数 \(N>\mathbf{0}\) 使得 \(\quad f(x) \geq \frac{N}{x-a} \quad(a<x \leq b)\) 则反常积分 \(\int_a^{b} f(x) d x\) 发散
定理 7(极限审敛法2)
设函数 \(f(x)\) 在区间 \((a, b]\) 上连续,且 \(f(x) \geq 0\) ,\(x=a\) 是瑕点.如果存在常数 \(\mathbf{0}<q<1, \quad\) 使得\(\lim _{x \rightarrow a^{+}}(x-a)^{q} f(x)\)存在,则反常积分 \(\int_{a}^{b} f(x) d x\) 收敛: 如果 \(\lim _{x \rightarrow a^{+}}(x-a) f(x)=d>0\left(\text { 或 } \lim _{x \rightarrow a^{+}}(x-a) f(x)=+\infty\right)\) 则反常积分 \(\int_{a}^{b} f(x) d x\) 发散.
对于无界函数的反常积分,当被积函数在所讨论的区间上可取正值又可取负值时,也有与定理5相类似的结论。
\(\Gamma\)函数
\(\Gamma\)函数定义
\(\Gamma\)函数属于区间无限的反常积分.
$() _{0}^{+} x^{} e^{-x} d x $
或者\(\Gamma(s)=\int_{0}^{+\infty} e^{-x} x^{s-1} d x,(s>0)\)
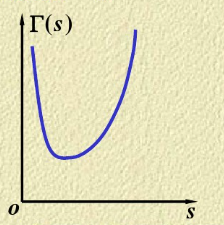
\(\Gamma\)函数的几个例子:
eg: \(\int_{0}^{+\infty} x^{4} e^{-x} d x=\Gamma(5)\)
eg: \(\int_{0}^{+\infty} \sqrt{x} e^{-x} d x=\Gamma\left(\frac{3}{2}\right)\)
\(\Gamma\)函数特点
- 积分区间为无穷区间;
- \(0<s<1\)时,被积函数在点 \(x=0\) 的右半邻域内无界. 点 \(x=0\) 是瑕点.
- \(\Gamma(s)=\int_{0}^{+\infty} e^{-x} x^{s-1} d x\) 对 \(s>0\) 均收敛.
- 由\(\Gamma(s)\)的图形,可知\(\Gamma(s)\)在\((0,+\infty)\)上连续
证明\(\Gamma\)函数在\(s>0\)均收敛
当 \(s-1<0\) 时,即\(0<s<1\)时,被积函数在点 \(x=0\) 的右半邻域内无界. 点 \(x=0\) 是瑕点. 设 \(I_{1}=\int_{0}^{1} e^{-x} x^{s-1} d x, \quad I_{2}=\int_{1}^{+\infty} e^{-x} x^{s-1} d x\) (1) 当 \(s \geq 1\) 时, \(I_{1}\) 是定积分 (2) \(0<s<1\) 时,\(\because e^{-x} \cdot x^{s-1}=\frac{1}{x^{1-s}} \cdot \frac{1}{e^{x}}<\frac{1}{x^{1-s}}\) 又\(\because 1- s<1 \therefore I_{1}=\int_{0}^{1} e^{-x} x^{s-1} d x\) 收敛.(比较审敛法2) \(\lim _{x \rightarrow+\infty} x^{2} \cdot\left(e^{-x} x^{s-1}\right)=\lim _{x \rightarrow+\infty} \frac{x^{s+1}}{e^{x}}=0\) \(\therefore I_{2}=\int_{1}^{+\infty} e^{-x} x^{s-1} d x\) 收敛. \(\quad(\) 极限审敛法)
由 (1),(2) 知 \(\Gamma(s)=\int_{0}^{+\infty} e^{-x} x^{s-1} d x\) 对 \(s>0\) 均收敛.
\(\Gamma\)函数性质
- 递推公式 \(\Gamma(\alpha+1)=\alpha \Gamma(\alpha)\),要求\(\alpha >0\) \(\Gamma(n+1)=n !\) \(\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}\)
- 当 \(s \rightarrow 0^{+}\) 时 \(, \Gamma(s) \rightarrow+\infty\)
- 余元公式 \(\Gamma(s) \Gamma(1-s)=\frac{\pi}{\sin \pi s}(0<s<1)\)
- \(\int_{0}^{+\infty} e^{-u^{2}} u^{t} d u=\frac{1}{2} \Gamma\left(\frac{1+t}{2}\right),(t>-1)\)
递推公式 \(\Gamma(s+1)=s \Gamma(s)(s>0)\)的证明 \(\Gamma(s+1)=\int_{0}^{+\infty} e^{-x} x^{(s+1)-1} d x\) \(=\int_{0}^{+\infty} e^{-x} x^{s} d x=\int_{0}^{+\infty} x^{s} d\left(-e^{-x}\right)\) \(=\left[x^{s}\left(-e^{-x}\right)\right]_{0}^{+\infty}-\int_{0}^{+\infty}\left(-e^{-x}\right) d\left(x^{s}\right)\) \(=\lim _{x \rightarrow+\infty} x^{s}\left(-e^{-x}\right)-0-\int_{0}^{+\infty}\left(-e^{-x}\right) s x^{s-1} d x\) \(=\underline{0}-0+s \int_{0}^{+\infty} e^{-x} x^{s-1} d x \quad(\text { 洛必达法则 })\) \(=s \Gamma(s)\)
当\(s \rightarrow 0^{+}\)时\(\Gamma(s) \rightarrow+\infty\)的证明 由(1)得: \(\Gamma(s)=\frac{\Gamma(s+1)}{s},(s>0)\) 令 \(s \rightarrow 0^{+}\) 取极限,得 \(\Gamma(s+1) \rightarrow \Gamma(1)=1\) \([\because \Gamma(s) \text { 在s }=1 \text { 连续 }]\) \(\therefore \Gamma(s) \rightarrow+\infty \quad\left(\text { 当 } s \rightarrow 0^{+} \text {时 }\right)\)
\(\Gamma(s) \Gamma(1-s)=\frac{\pi}{\sin \pi s},(0<s<1)\)(余元公式)不证,但是可以比较轻松的得到\(\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}\) 取 \(s=\frac{1}{2},\) 代入得 \(\Gamma\left(\frac{1}{2}\right) \Gamma\left(\frac{1}{2}\right)=\frac{\pi}{\sin \frac{\pi}{2}}=\pi\) \(\therefore \quad \Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}\)
\(\int_{0}^{+\infty} e^{-u^{2}} u^{t} d u=\frac{1}{2} \Gamma\left(\frac{1+t}{2}\right),(t>-1)\)的证明 (\(\Gamma\)型向泊松型的变换) \(\Gamma(s)=\int_{0}^{+\infty} e^{-x} x^{s-1} d x\) \(\overset{\text { 令 }{x}=u^{2} }{=} \int_{0}^{+\infty} e^{-u^{2}} u^{2(s-1)} 2 u d u\) (换积分符号不影响函数的自变量) \(=2 \int_{0}^{+\infty} e^{-u^{2}} u^{2 s-1} d u\) (自变量换为t) \(\overset{\text { 记 } t= 2 s-1 }{=} 2 \int_{0}^{+\infty} e^{-u^{2}} u^{t} d u\) (泊松型表示为\(\Gamma\)函数) \(=\int_{0}^{+\infty} e^{-u^{2}} u^{t-1} 2 u d u\) \(=\int_{0}^{+\infty} e^{-u^{2}} u^{t-1} d\left(u^{2}\right)\) \(=\int_{0}^{+\infty} e^{-u^{2}}\left(u^{2}\right)^{\frac{1}{2}(t-1)} d\left(u^{2}\right)\) \(=\int_{0}^{+\infty} e^{-u^{2}}\left(u^{2}\right)^{\frac{1}{2}(t+1)-1} d\left(u^{2}\right)\) \(\overset{x=u^2}{=}\int_{0}^{+\infty} e^{-x} x^{\frac{1}{2}(t+1)-1} d x=\Gamma\left(\frac{1+t}{2}\right)\) 综上\(\therefore \int_{0}^{+\infty} e^{-u^{2}} u^{t} d u=\frac{1}{2} \Gamma\left(\frac{1+t}{2}\right),(t>-1)\)
高斯积分与泊松积分

\(\int_{-\infty}^{+\infty} \mathrm{e}^{-x^{2}} \mathrm{d} x=2 \int_{0}^{+\infty} \mathrm{e}^{-x^{2}} \mathrm{d} x=\sqrt{\pi}\)
由于被积函数是一个偶函数(如下图所示),0到\(+\infty\)的积分显然就是\(\frac {\sqrt{ \pi}}{2}\).
(0到\(+\infty\)上的积分又叫泊松积分:Euler-Poisson积分)
高斯积分可由\(\Gamma\)函数可以算出
\(\Gamma\left(\frac{1}{2}\right)=\int_{0}^{\infty} \frac{1}{\sqrt{x} e^{x}} d x=\int_{-\infty}^{\infty} e^{-x^{2}} d x=\sqrt{\pi}\)
泊松型积分可表示为\(\Gamma\)函数
\(2 \int_{0}^{+\infty} e^{-u^{2}} u^{t} d u\) \(=\int_{0}^{+\infty} e^{-u^{2}} u^{t-1} 2 u d u\) \(=\int_{0}^{+\infty} e^{-u^{2}} u^{t-1} d\left(u^{2}\right)\) \(=\int_{0}^{+\infty} e^{-u^{2}}\left(u^{2}\right)^{\frac{1}{2}(t-1)} d\left(u^{2}\right)\) \(=\int_{0}^{+\infty} e^{-u^{2}}\left(u^{2}\right)^{\frac{1}{2}(t+1)-1} d\left(u^{2}\right)\) \(\overset{x=u^2}{=}\int_{0}^{+\infty} e^{-x} x^{\frac{1}{2}(t+1)-1} d x=\Gamma\left(\frac{1+t}{2}\right)\)
即\(\int_{0}^{+\infty} e^{-u^{2}} u^{t} d u\) \(=\frac{1}{2}\Gamma\left(\frac{1+t}{2}\right)\)
即泊松积分都可以化为\(\Gamma\)函数求解。
而泊松积分在概率论中会有应用(计算正态分布、瑞利分布等的分布函数、期望、方差等)
积分不等式的证明
证明某积分不等式,是考研中经常见到的问题. 处理这类问题有三种方法. (1)将要证的某某 > 0(或 \(\geqslant0\)) 的一边变成变限函数,用微分学的办法证此不等式(例如 用单调性,最值,拉格朗日中值定理,拉格朗日余项泰勒公式等等),这是考研中经常用到的方法. (2) 设要证的是 \(\int_{a}^{b} f(x) \mathrm{d} x \geqslant \int_{a}^{b} g(x) \mathrm{d} x(a<b),\)先去证当 \(a \leqslant x \leqslant b\) 时 \(f(x) \geqslant g(x),\) 那么再由积分不等式的性质便有 \(\int_{a}^{b} f(x) \mathrm{d} x \geqslant \int_{a}^{b} g(x) \mathrm{d} x\) 如果要证的是\(\int_{a}^{b} f(x) \mathrm{d} x>\int_{a}^{b} g(x) \mathrm{d} x(a<b), \text {先去证当 } a \leqslant x \leqslant b \text { 时 } f(x) \text { 与 } g(x)\)都连续,且 \(f(x) \geqslant g(x),\) 并且至少存在一点 \(x_{1} \in[a, b]\) 使 \(f\left(x_{1}\right)>g\left(x_{1}\right),\) 则由定理 便有 \(\int_{a}^{b} f(x) \mathrm{d} x>\int_{a}^{b} g(x) \mathrm{d} x .\) 考试中常见的是严格不等式情形. (3) 利用积分性质,例如积分中值定理、积分变量代换、分部积分等方法,经变形并计算。 如果一个式子有积分号,一个没有积分号,要比较它们的大小,可以将有积分号的那一个用积分中偵定理化成没有积分号的,或者将没有积分号的套上积分号,在积分号里面比较大小. 有时两个积分的积分区间不一样,那么是否能通过变量代换将它们变成一样,从而比较被积既数的大小等等
