高等数学-一元积分学-定积分与反常积分

定积分与积分函数

求定积分

分部积分法求定积分

例1

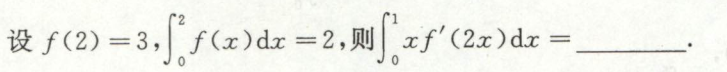
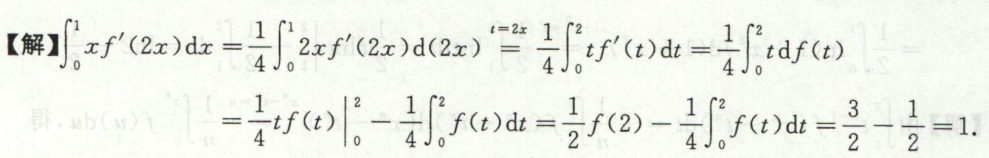
例2

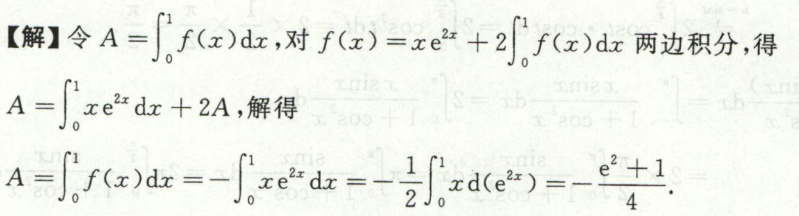
例3

例4

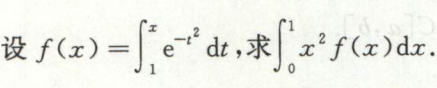
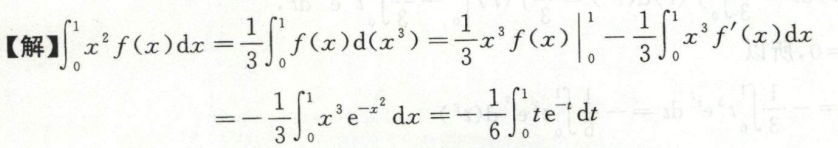
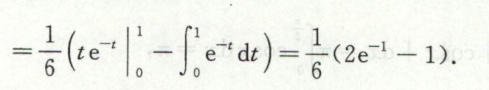
例5

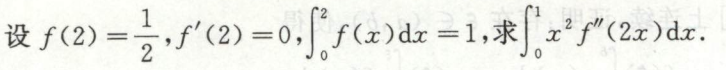
例6

例7

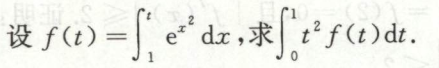
例8

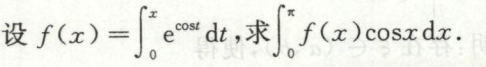
换元法求定积分

常规换元法

例1

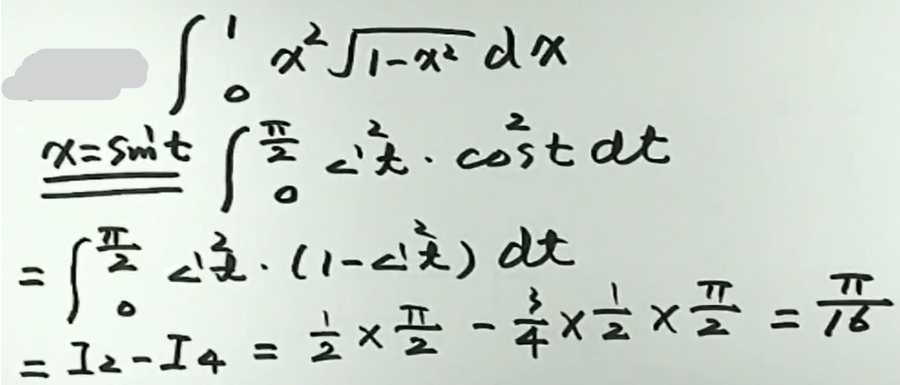
例2

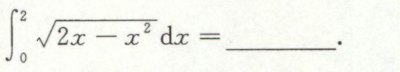
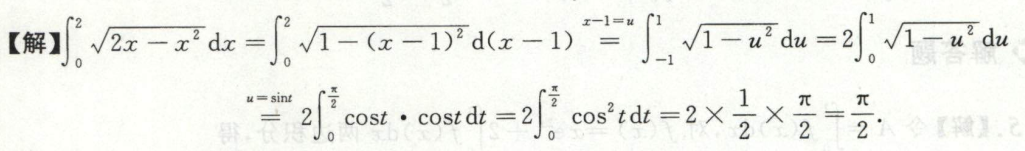
例3

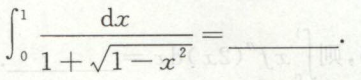
例4

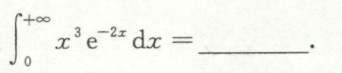
例5

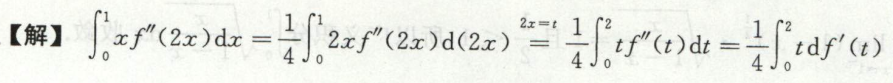
例6

例7

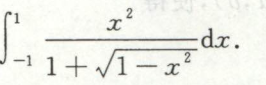
例8

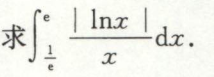
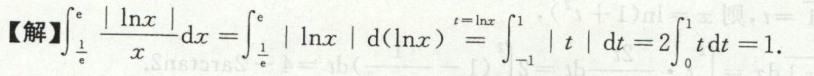
例9

例10

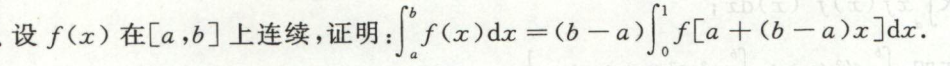
例11

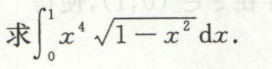
例12

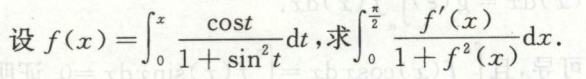
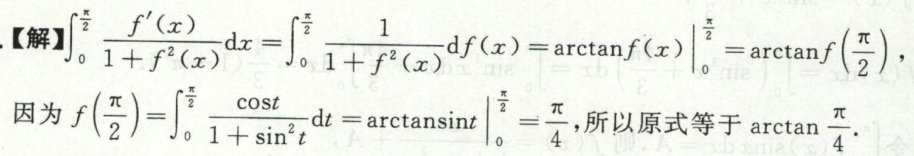
例13

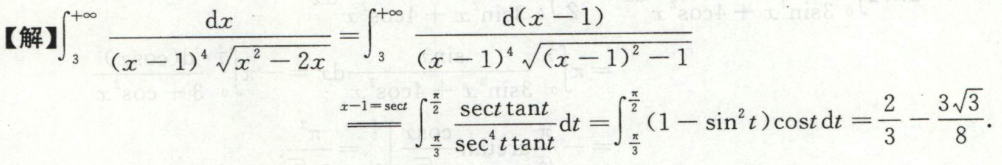
例14

例15

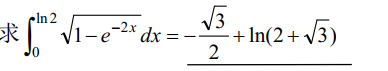
解：换元法：$\mathrm{设}t=e^{-2x}$，然后设$u=\sqrt{1-t}$求解

对调区间上下限的换元法

例1

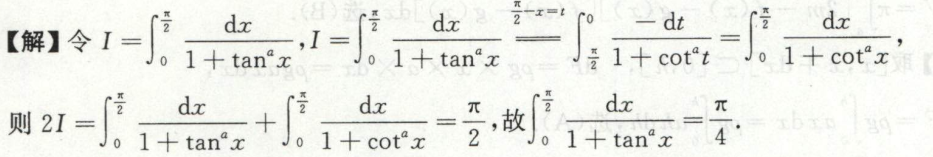
例2

例3

方法一:递推法

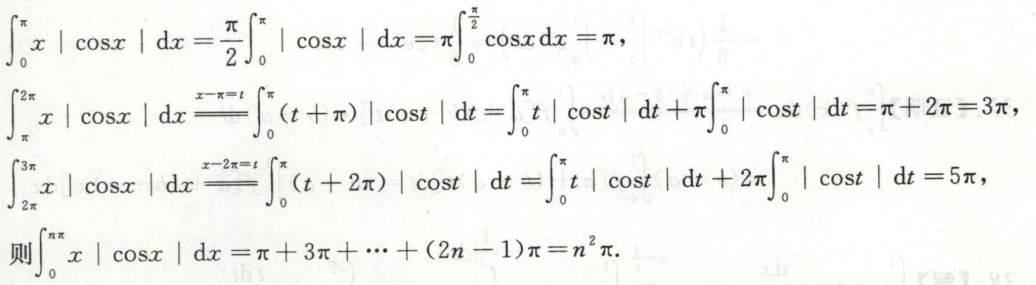
方法二:对调区间上下限的换元

倒数的换元法

例1

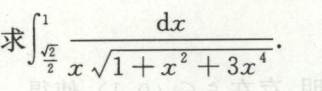
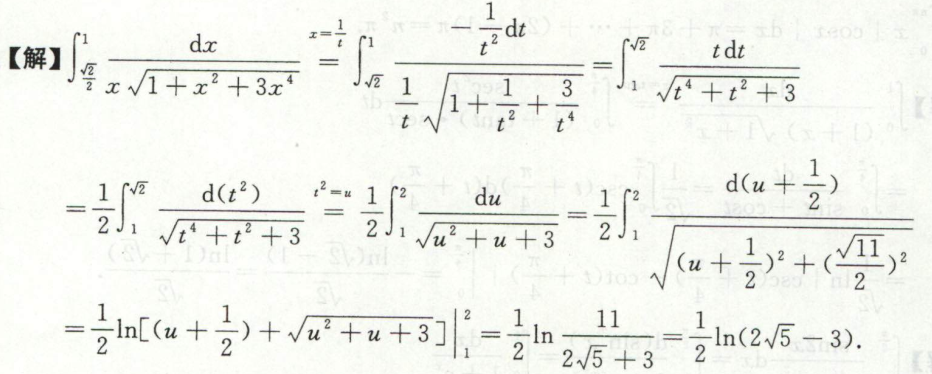
根据奇偶性和周期性求定积分

根据区间的对称性、函数的奇偶性求定积分；根据函数的周期性求定积分

例1

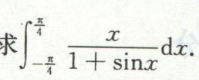
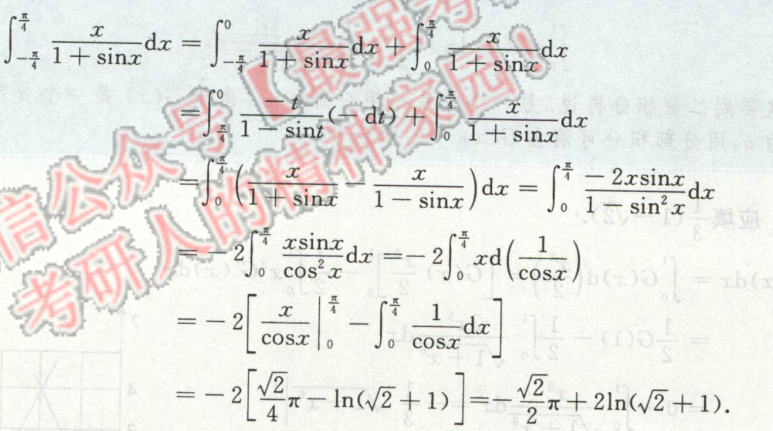
例2

例3

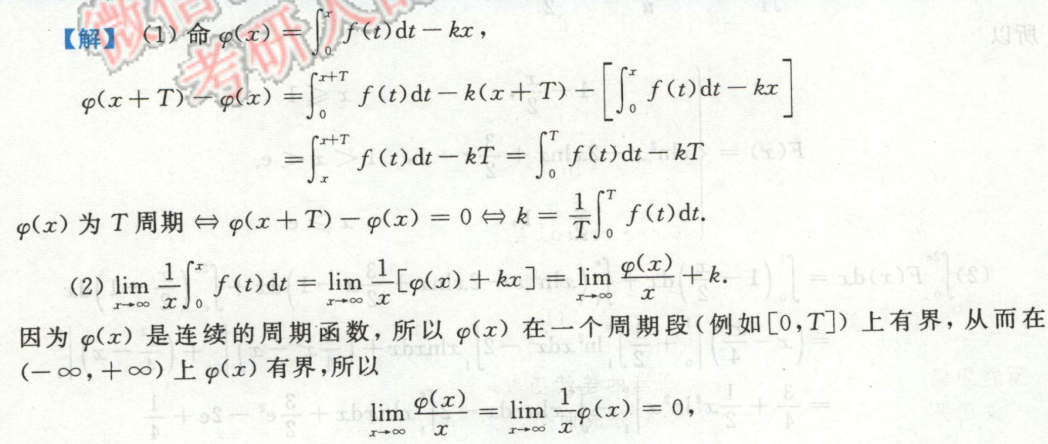
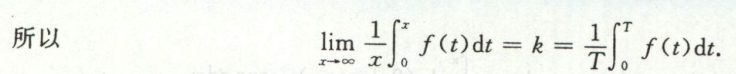
例4

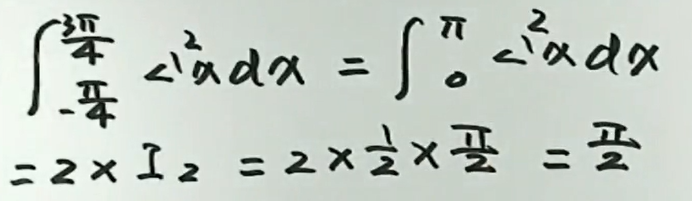
周期函数,平移上下限后可以使用华里士公式

例5

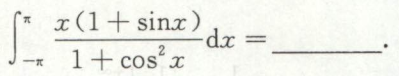
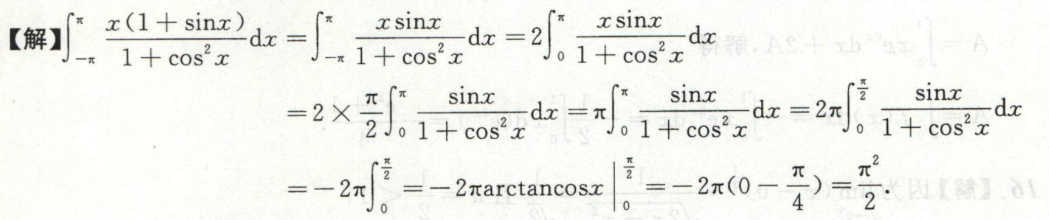
例6

例7

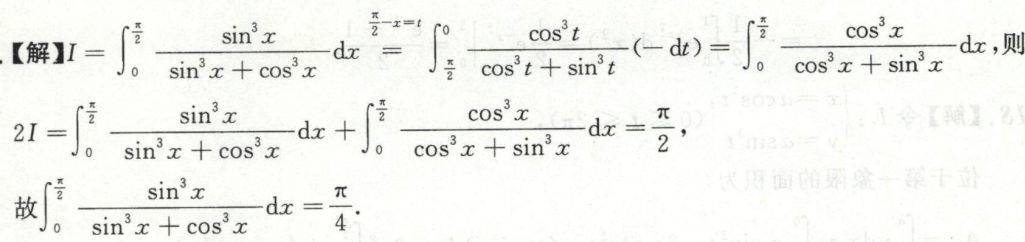
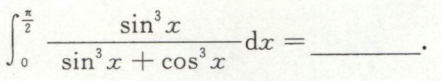
例8

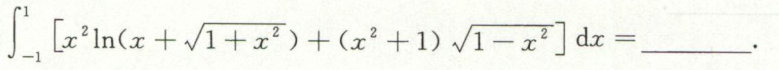
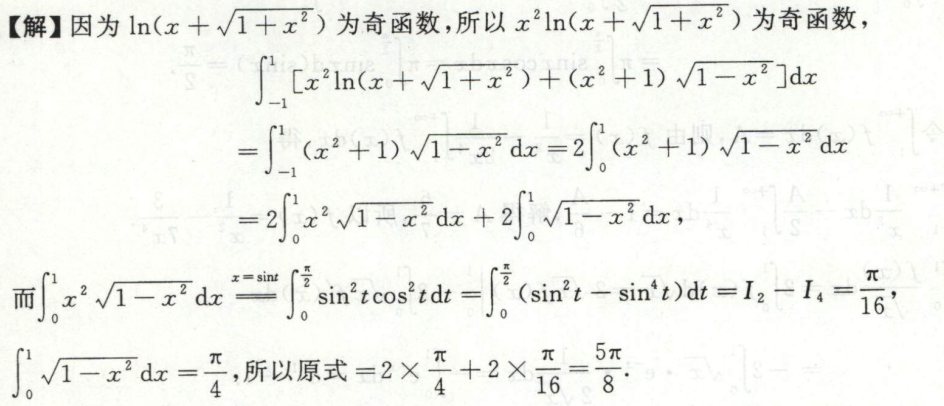
例9

例10

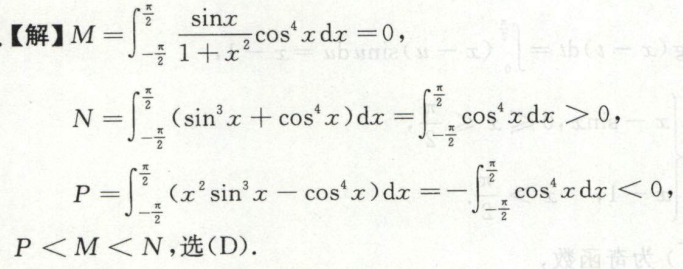
例11

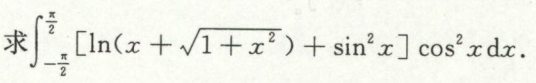
例12

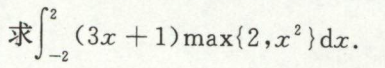
例13

例14

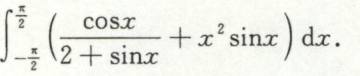
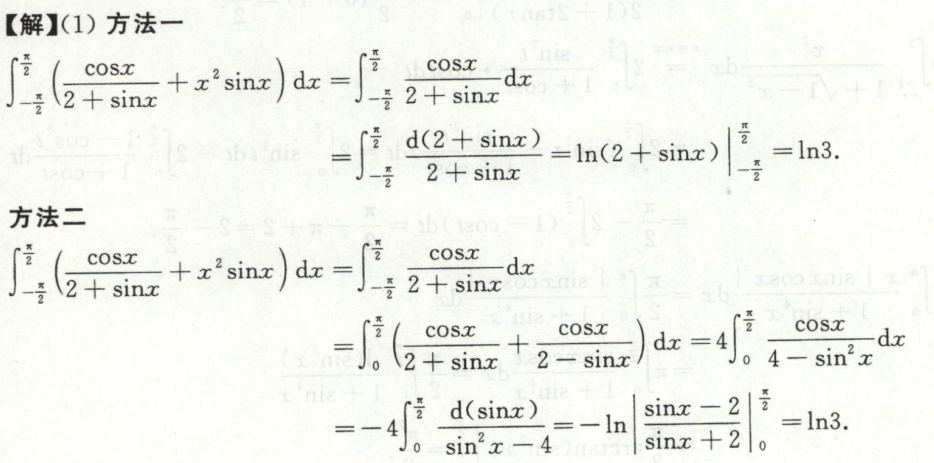
例15

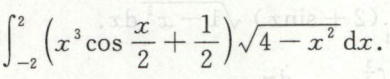
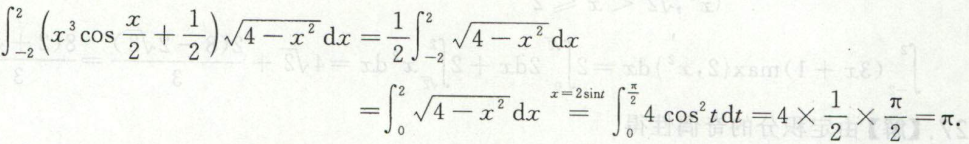
求分段函数的定积分

给f(x)为分段表达式，应按f(x)的分段，分段做定积分；由于积分的上限为x，所以应对x的范围作讨论才能选取分段

例1

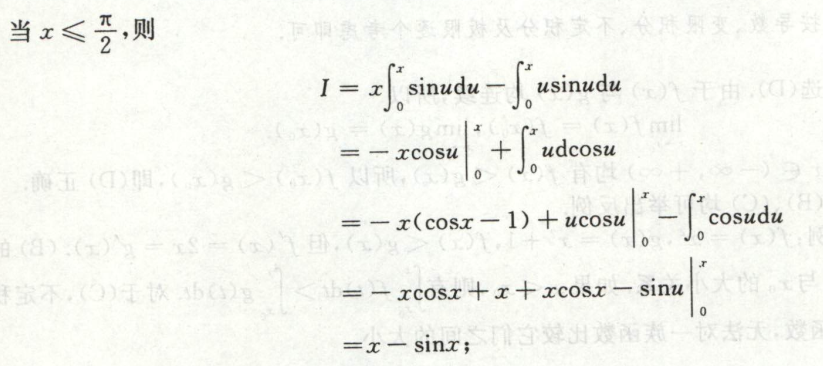
例2

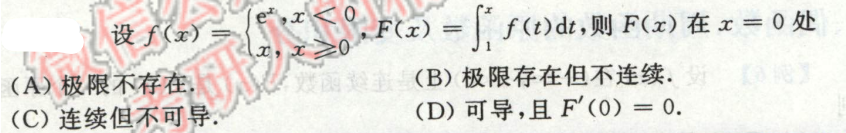
例3

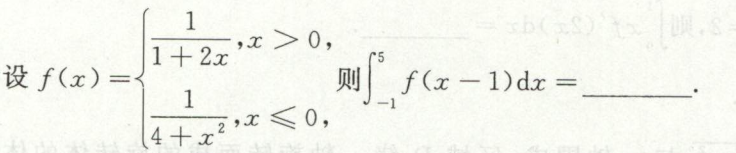
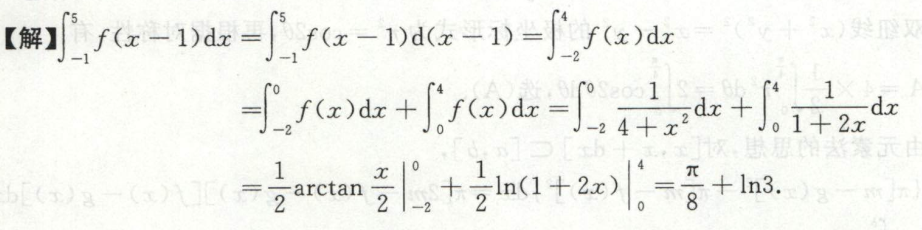
例6

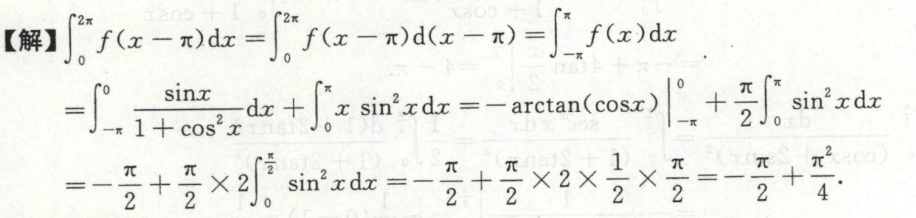
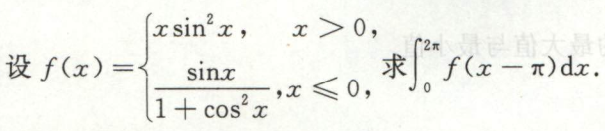
求三角函数的定积分

例1

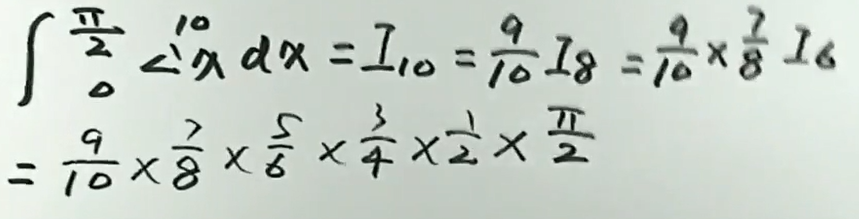
此题是${\int }_0^{\frac{\pi }{2}}f(\sin x)dx={\int }_0^{\frac{\pi }{2}}f(\cos x)dx$的推广

华里士公式：$I_n={\int }_0^{\frac{\pi }{2}}{\sin }^{n}x\mathrm{d}x={\int }_0^{\frac{\pi }{2}}{\cos }^{n}x\mathrm{d}x=\{\begin{array}{lr}\frac{n-1}{n}\cdot \frac{n-3}{n-2}\cdot \cdots \cdot \frac{1}{2}\cdot \frac{\pi }{2},& \text{ 当 }n\text{ 为正偶数 }\\ \frac{n-1}{n}\cdot \frac{n-3}{n-2}\cdots \cdots \frac{2}{3}\cdot 1,& \text{ 当 }n\text{ 为大于 }1\text{ 的正奇数. }\end{array}$ 即$\{\begin{array}{rl}& I_n=\frac{n-1}{n}{I}_{n-2}\\ & I_0=\frac{\pi }{2}\\ & I_1=1\end{array}$

例2

例3

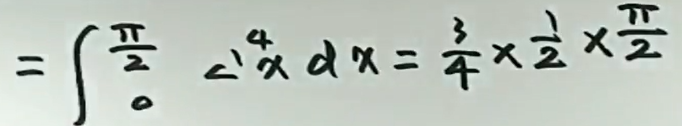
例4

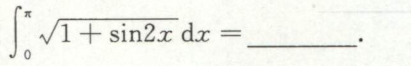
例5

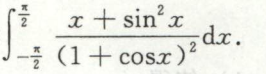
例6

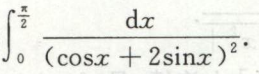
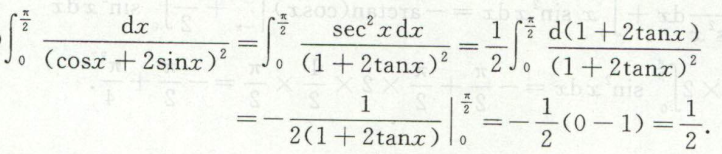
例7

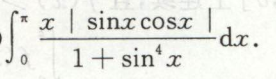
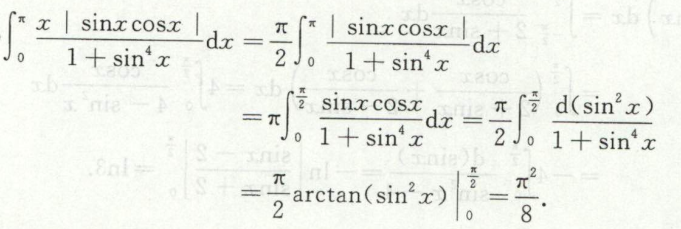
求简单无理分式的定积分

定积分化简根式时要保留绝对值。（一般是三角替换的时候）

例1

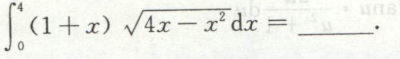
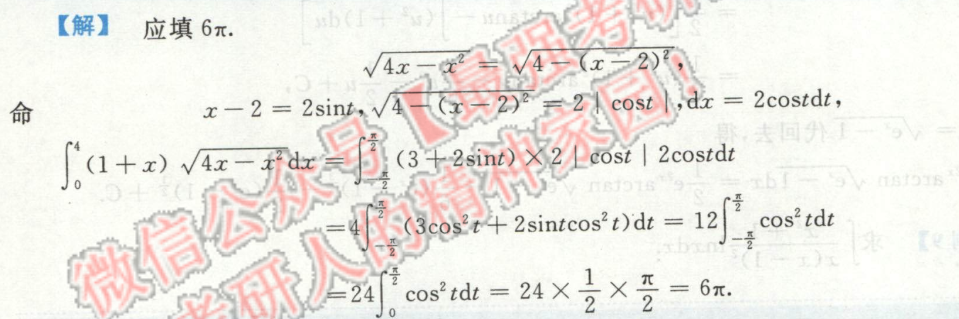
求含导数或变限函数的积分

带变限函数的积分有两种方法：可以化为2重积分，或者使用分部积分去掉一次积分

含导数的积分一般使用分部积分求解

例1

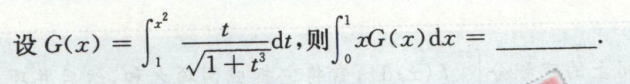
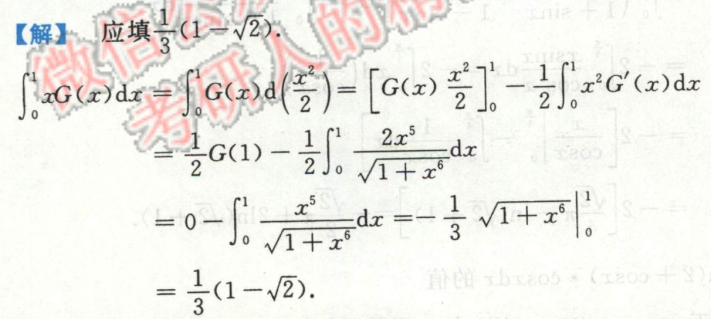
例2

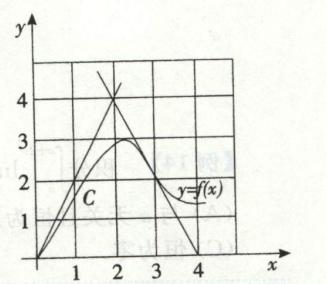
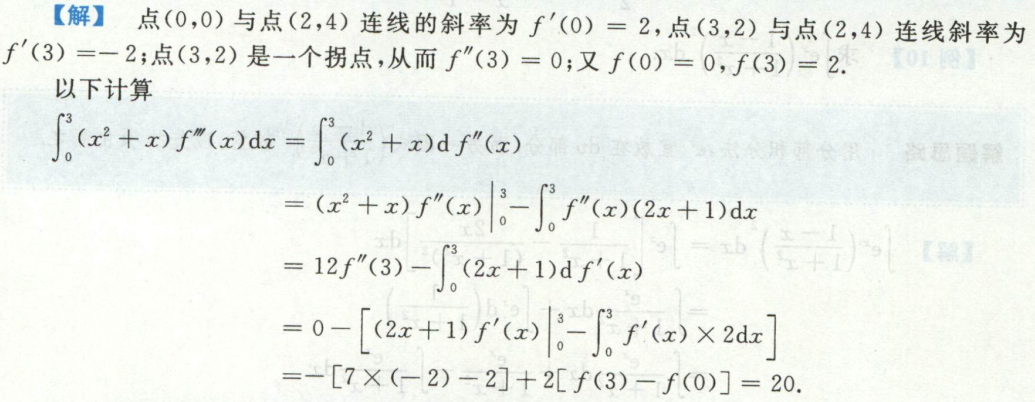
例3

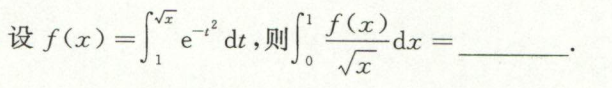
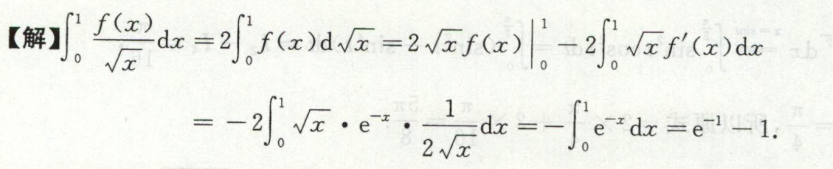
求带参带绝对值的定积分

例1

根据积分确定函数

例1

例2

例3

例4

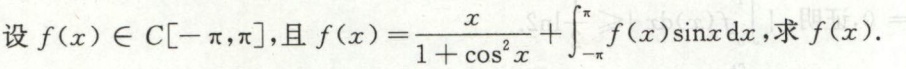
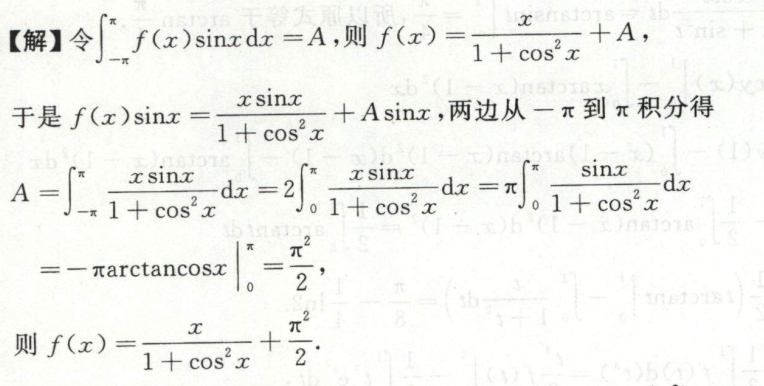
求变限积分函数

求变限积分

例1

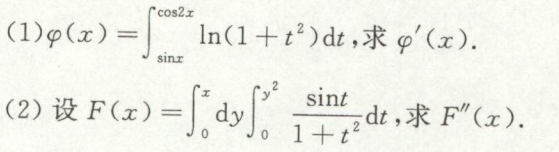
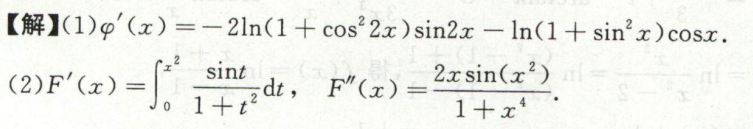
例2

求含变限积分的极限

求极限

根据定积分定义求极限

分子齐次，分母齐次，使用定积分的定义来求极限。

分子或分母，有一个不齐，使用夹逼定理求极限

例1

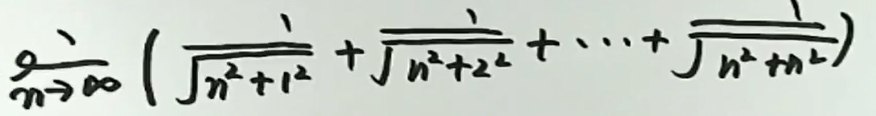
例2

例3

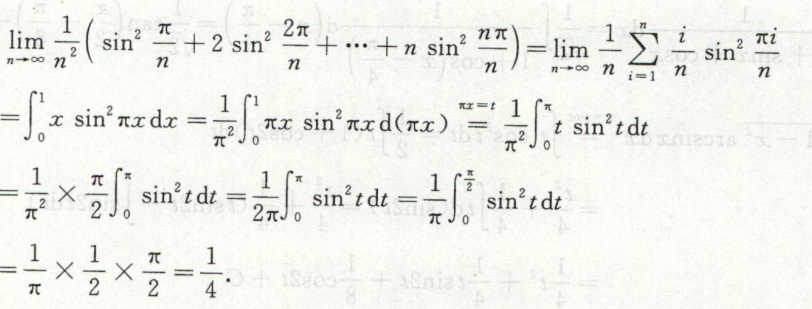
例4

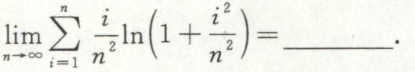
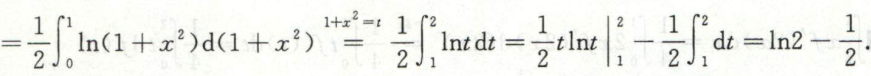
求含定积分的极限

例1

求含变限积分的极限

例1

例2

例3

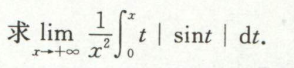
变限积分求参数

例1

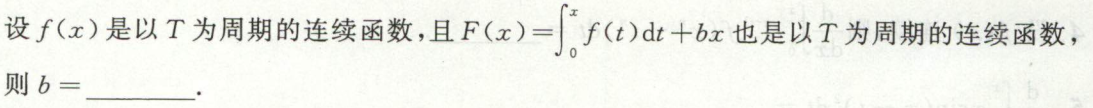
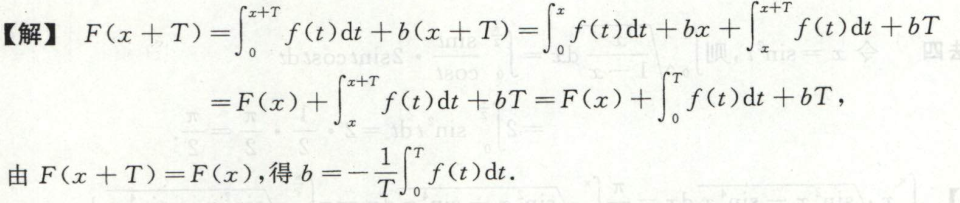
变限积分函数求导数

例1

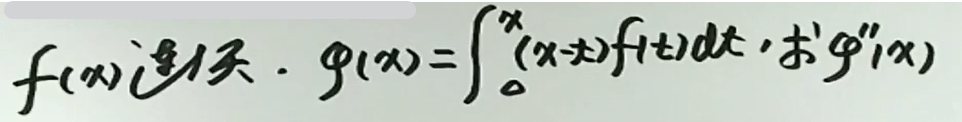
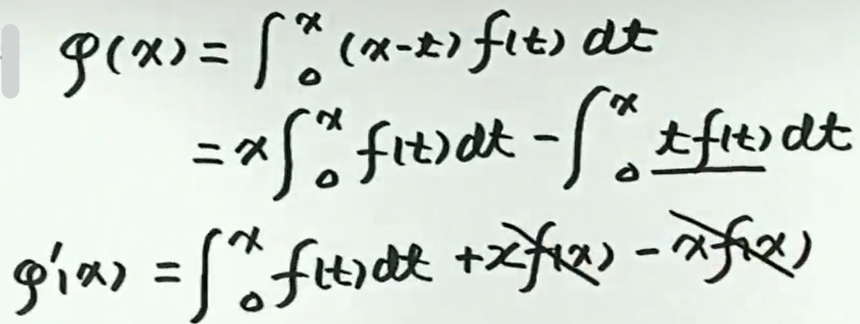
例2

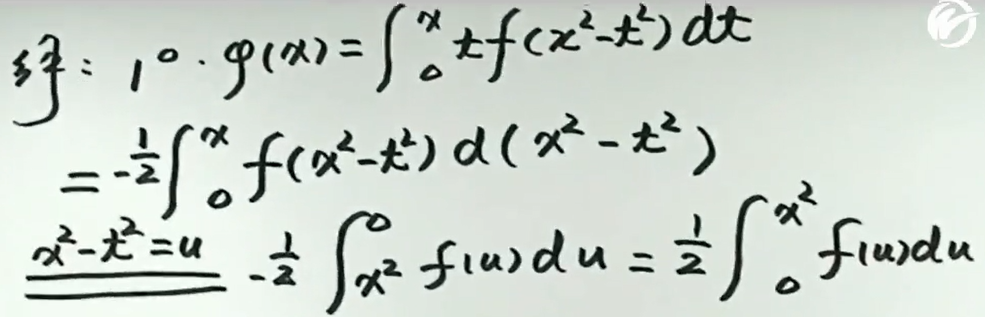
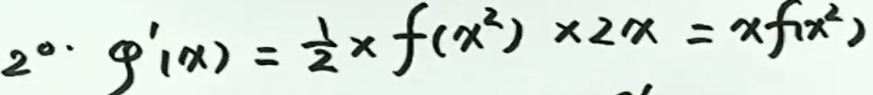
例3

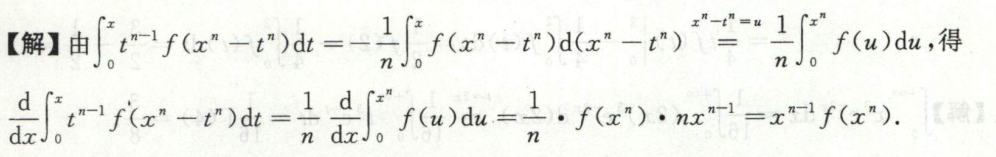
例4

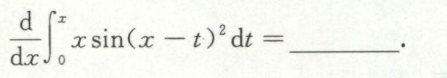
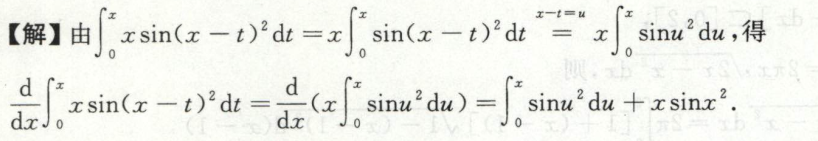
例5

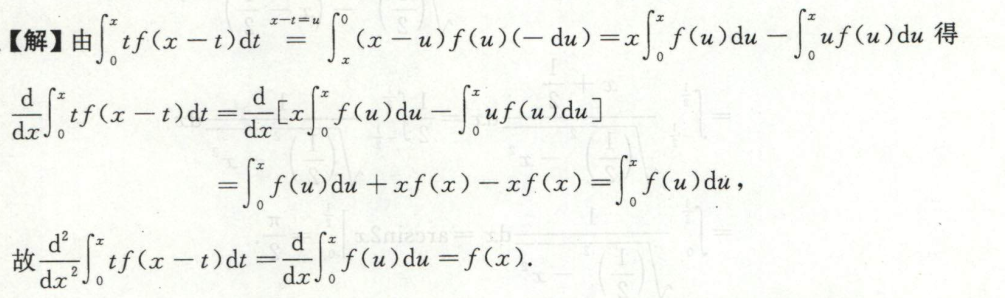
变限积分函数求最值

例1

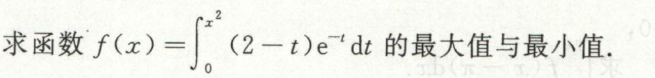
定积分与原函数的存在性判断

例1

函数存在原函数的前提条件是要连续。虽然不连续，但是只有有限个间断点，这样的函数是可积的（可以拆成几个连续的区间）。是否可导可根据定义或者左右导数存在且相等来看。

证明题

求证存在$\xi$使等式成立

零点定理求证存在$\xi$使等式成立

例1

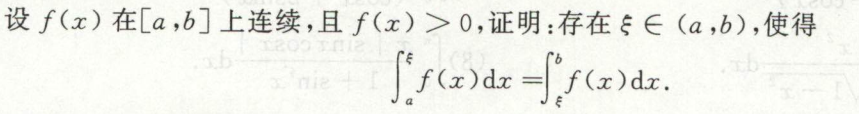
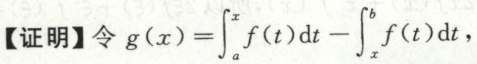
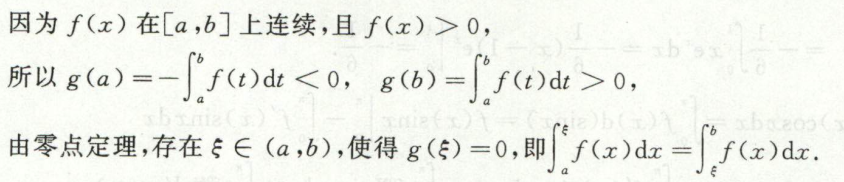
罗尔定理求证存在$\xi$使等式成立

例1

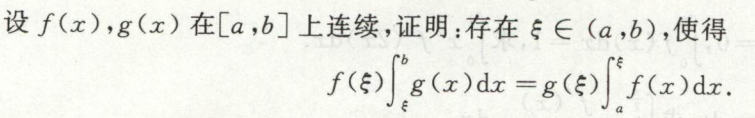
例2

泰勒公式证明存在$\xi$使等式成立

例1

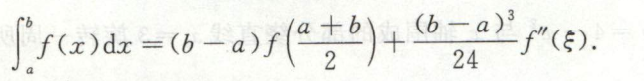
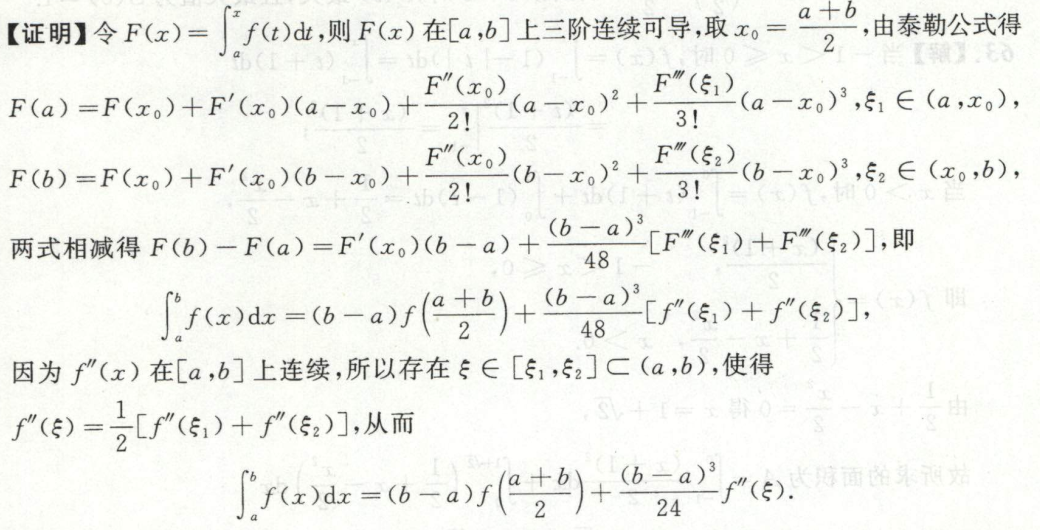
积分中值定理求证存在$\xi$使等式成立

例1

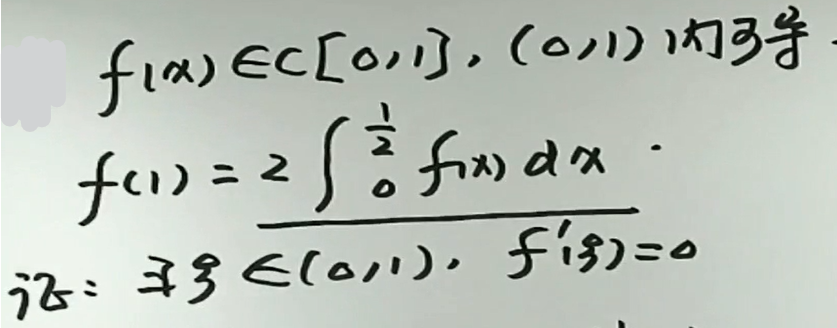
例2

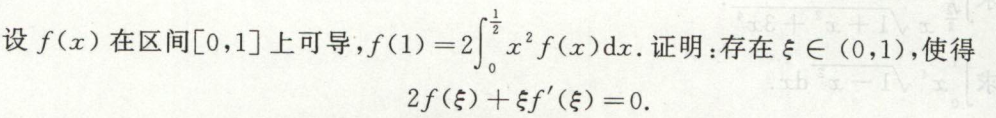
变限积分函数证存在$\xi$使等式成立

注意,如果要证明的是开区间内存在点,使等式成立,则不能使用积分中值定理.积分中值定理的结论是闭区间内存在点,满足条件

要证明的是开区间内存在点,使等式成立,应设变限积分函数来证.

积分中值定理有开区间和闭区间两种题目，开区间的话用到的结论是积分中值定理的推广，要写过程，用拉格朗日证明，所以要写出变上限积分，在原函数之一的基础上进行拉格朗日证明，和拉格朗日一样最后取到开区间；闭区间的话就是积分中值定理本身，不用写出证明过程，但是本身证明用的是介值定理，所以积分中值定理本身是闭区间

问的是开区间不是拉格朗日就是罗尔，就看已知几个相等

例1

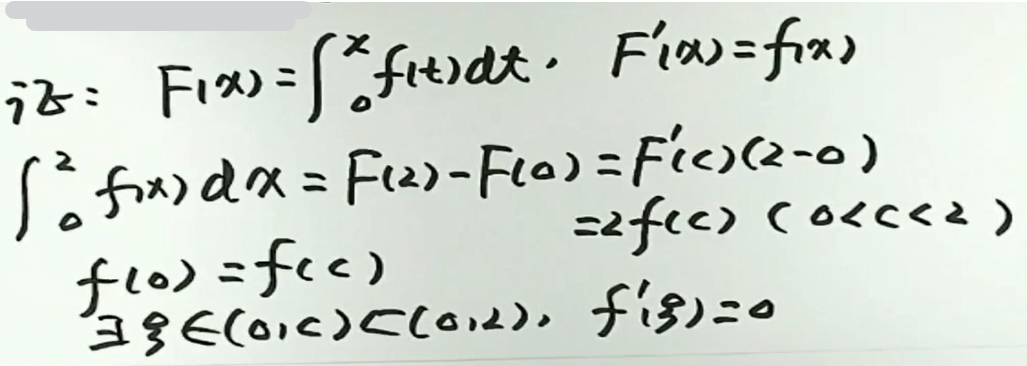
例2

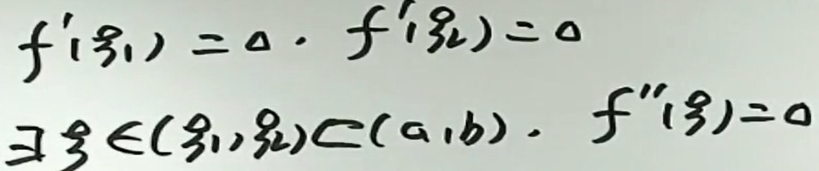
例3

例4

变限积分及其导数的奇偶性、周期性

由F（x）的奇偶性，周期性推断∫（x）的相应性质，用到微分学的性质； 反过来，由f（x）的奇偶性、周期性，推断F（x）的相应性质，可能会想到用不定积分，但是不定积分只能用来作为运算，不能用来讨论性质，应该用变上限函数来表示f（x）的某个原函数，用它来讨论原函数的性质

结论：

f->F

奇函数的（变上限）积分是偶函数；偶函数仅当从0开始的（变上限）积分是奇函数。

F->f

原函数是奇函数，求导是偶函数；原函数是偶函数，求导是奇函数。

例1

例2

例3

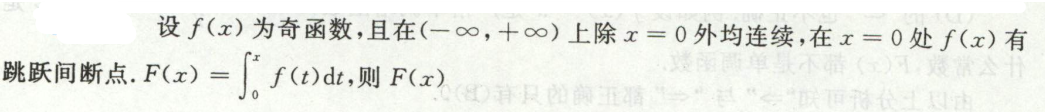
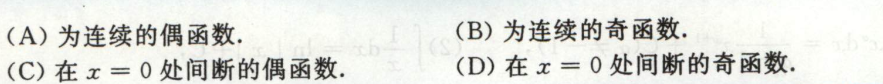
例4

例5

例6

积分等式的证明

例1

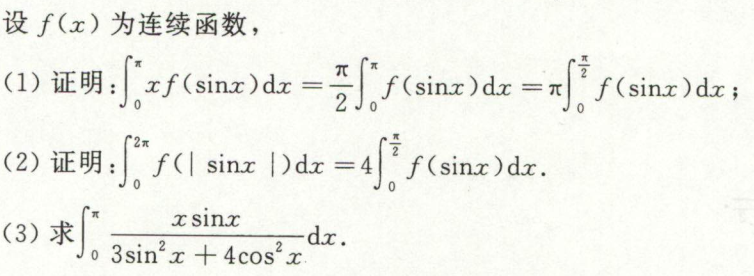
例2

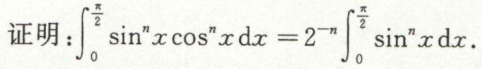
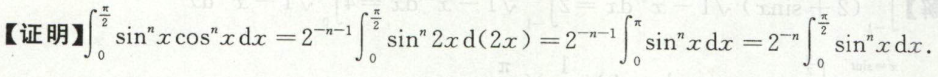
积分不等式的证明

积分的比较

例1

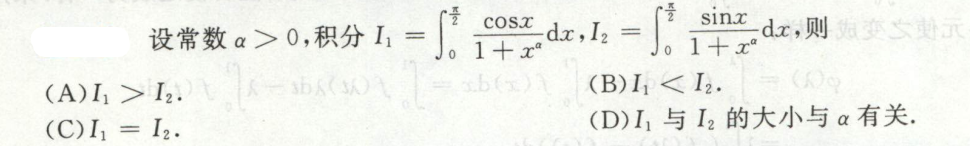
例2

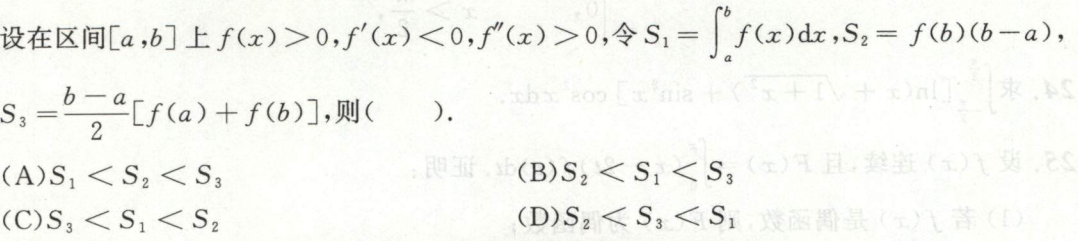
变限积分函数单调性与单调区间的判断

一个带积分号的函数,和另一个不带积分号的函数的比较,有两种办法:

• 用积分中值定理,将有积分号的化为无积分号的
• 将没有积分号的套上积分号

例1

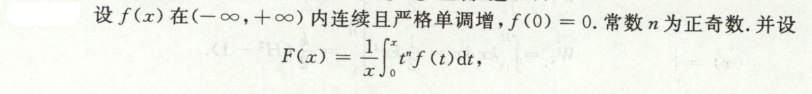
例2

积分不等式的证明

例1

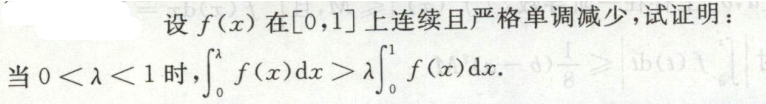
例2

例3

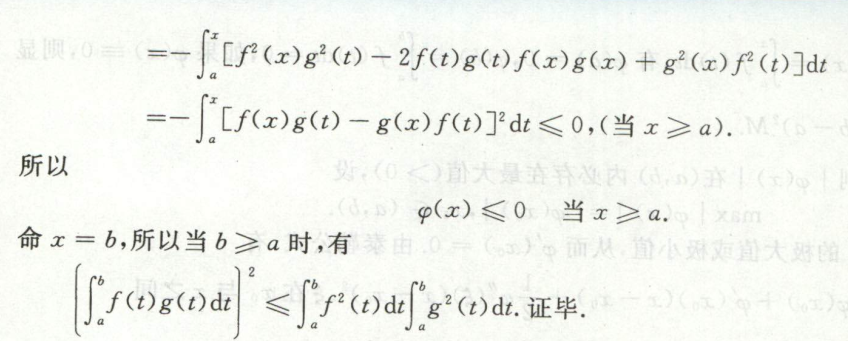
例4

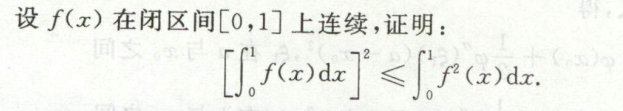
例5

例6

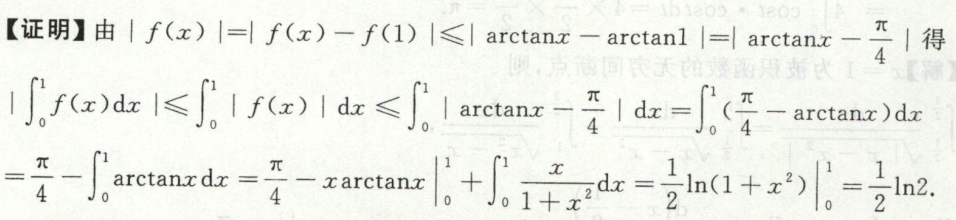
例7

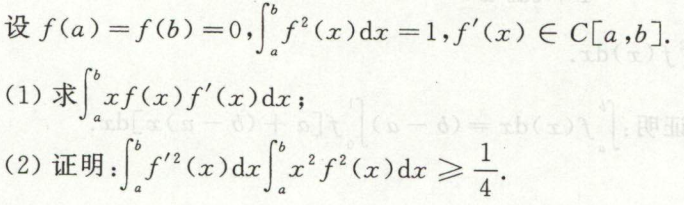
例8

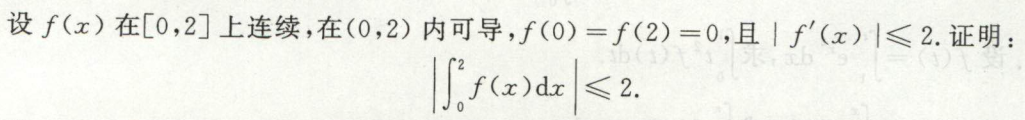
零点问题

零点问题,或者方程根的讨论

与微分学中类似，定积分与变限积分中也有零点问题处理的办法

• 一是化成变限积分看成变限的函数，用微分学中讲到的办法
• 二是利用积分中值定理

例1

例2

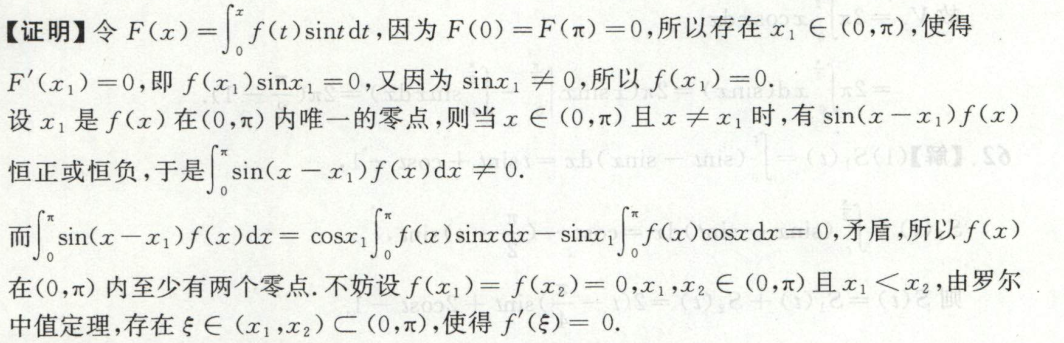
反常积分

反常积分的识别

区间无限的反常积分:只要一看积分限有$\mathrm{\infty }$,便知这是无穷区间上的反常积分

无界函数的反常积分:般是看被积函数是否有使其分母为零的点。但这句话既不充分也不必要.

例1

例2

反常积分的判敛及求解

通过计算来求解及判敛

例1

例2

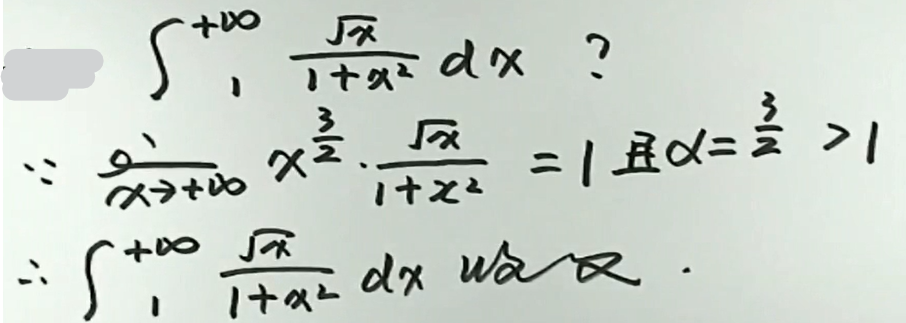
例3

要想对无穷积分使用定积分在对称区间上的性质,首先要满足无穷积分收敛才行.

例4

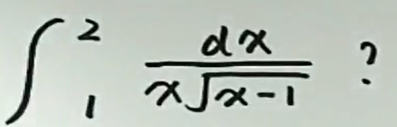
例5

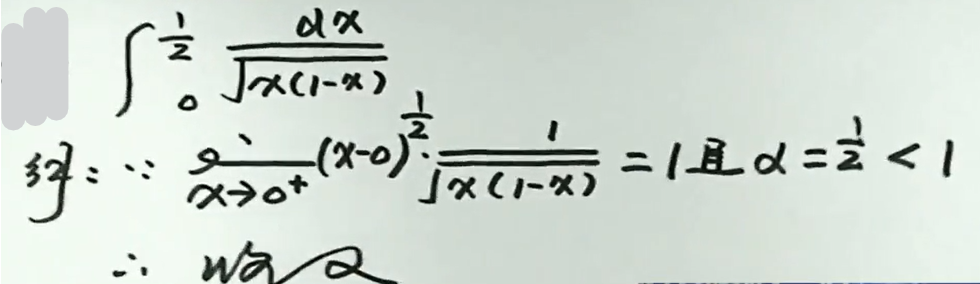
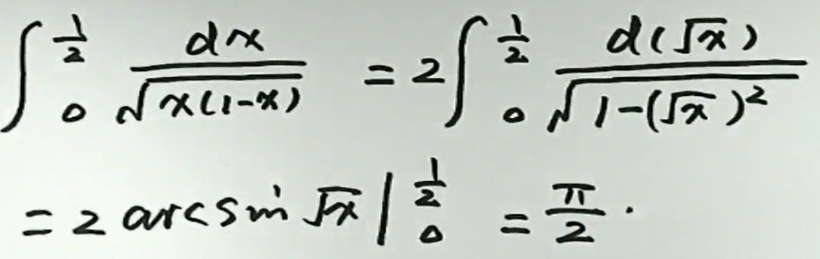
例6

例7

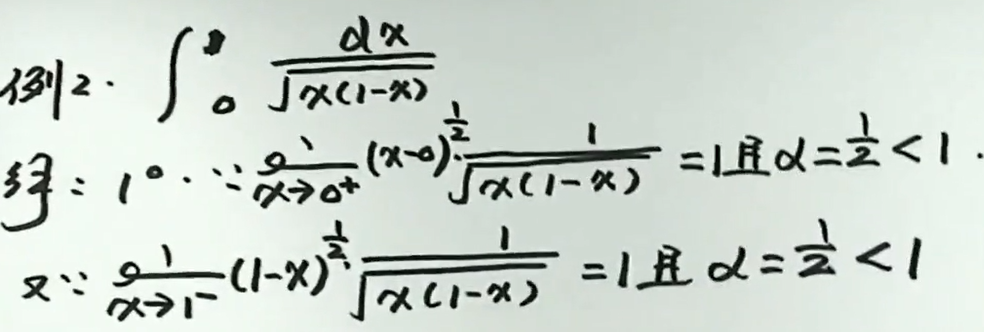
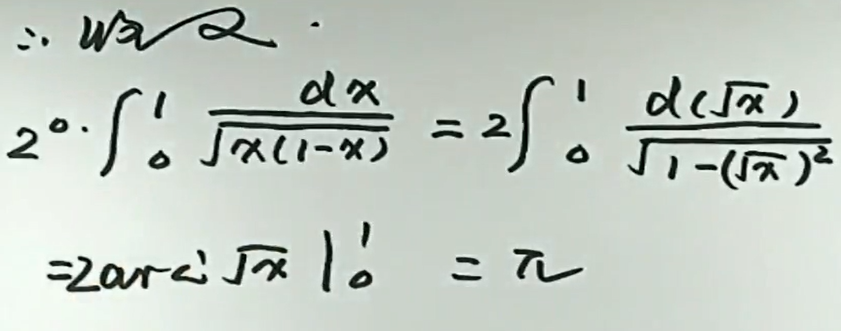
例8

例9

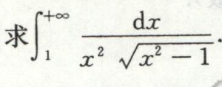
例10

通过计算这两个积分可知都收敛,答案选A

例11

例12

例13

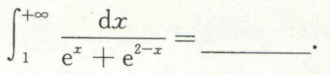
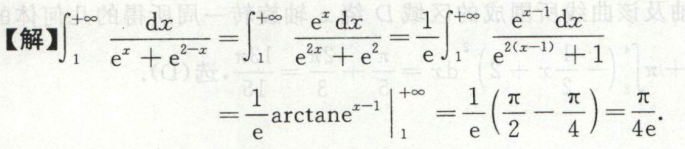
例14

例15

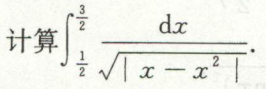
反常积分的非计算判敛方式(审敛)

例1

此题没弄懂.//TODO

例2

判别反常积分 ${\int }_1^{+\mathrm{\infty }}\frac{dx}{\sqrt[3]{x^4+1}}$ 的收敛性. 解 $\because$当 $x\in [1,+\mathrm{\infty })$ 时 $0<\frac{1}{\sqrt[3]{x^4+1}}<\frac{1}{\sqrt[3]{x^4}}=\frac{1}{x^{4/3}},p=\frac{4}{3}>1$ $\therefore$ 反常积分 ${\int }_1^{+\mathrm{\infty }}\frac{dx}{\sqrt[3]{x^4+1}}$ 收敛.

例3

判别反常积分 ${\int }_1^{+\mathrm{\infty }}\frac{dx}{x\sqrt{1+x^2}}$ 的收敛性. 解 $\because \underset{x\to +\mathrm{\infty }}{lim}{x}^2\cdot \frac{1}{x\sqrt{1+x^2}}=1,p=2>1$ $\therefore$ 所给反常积分收敛.(极限审敛法1)

例4

判别反常积分 ${\int }_1^{+\mathrm{\infty }}\frac{x^{3/2}}{1+x^2}dx$ 的收敛性 $\underset{x\to +\mathrm{\infty }}{lim}x\frac{x^{3/2}}{1+x^2}=\underset{x\to +\mathrm{\infty }}{lim}\frac{x^2\sqrt{x}}{1+x^2}=+\mathrm{\infty }$ 所给反常积分发散.（极限审敛法 1）

例5

判别反常积分 ${\int }_1^{+\mathrm{\infty }}\frac{\arctan x}{x}dx$ 的收敛性. 解 $\underset{x\to +\mathrm{\infty }}{lim}x\frac{\arctan x}{x}=\underset{x\to +\mathrm{\infty }}{lim}\arctan x=\frac{\pi }{2}>0$ $\therefore$ 所给反常积分发散.(极限审敘法 1）

例6

判别反常积分 ${\int }_0^{+\mathrm{\infty }}{e}^{-ax}\sin bxdx(a,b$ 都是常数 a > 0) 的收敛性. 解 $\because |e^{-ax}\sin bx|\le e^{-ax},$ 而 ${\int }_0^{+\mathrm{\infty }}{e}^{-ax}dx$ 收敘. $[\because {\int }_0^{+\mathrm{\infty }}{e}^{-ax}dx={[-\frac{1}{a}{e}^{-ax}]}_0^{+\mathrm{\infty }}=0-(-\frac{1}{a})=\frac{1}{a}]$ $\therefore {\int }_0^{+\mathrm{\infty }}|e^{-ax}\sin bx|dx$ 收敛. $(\text{ 比较审敛法 }1)$ $\therefore {\int }_0^{+\mathrm{\infty }}{e}^{-ax}\sin bxdx$ 收敛

例7

$$判别反常积分 ${\int }_1^3\frac{dx}{\ln x}$ 的收敛性. 解 $\because \underset{x\to 1^{+}}{lim}\frac{1}{\ln x}=+\mathrm{\infty }\therefore x=1$ 是瑕点 $\underset{x\to 1^{+}}{lim}(x-1)\frac{1}{\ln x}=\underset{x\to 1^{+}}{lim}\frac{x-1}{\ln x}\left(\frac{0}{0}\right)=$ $=\underset{x\to 1^{+}}{lim}\frac{1}{\frac{1}{n}}(\text{ 洛必达法则 })$ $\begin{array}{rl}& =1>0\end{array}$ ：反常积分${\int }_1^3\frac{dx}{\ln x}$ 发散. (极限审敛法2)

例8

$\begin{array}{rl}& \begin{array}{c}\text{判别椭圆积分 }{\int }_0^1\frac{1}{\sqrt{(1-x^2)(1-k^2{x}^2)}}dx\text{ 的收敛性 }\\ \text{ 这里 }|k|<1\end{array}\\ & \because \underset{x\to 1^{-}}{lim}\frac{1}{\sqrt{(1-x^2)(1-k^2{x}^2)}}=+\mathrm{\infty }\therefore x=1\text{ 是瑕点 }\\ & \because \underset{x\to 1^{-}}{lim}(1-x{)}^{\frac{1}{2}}\frac{1}{\sqrt{(1-x^2)(1-k^2{x}^2)}}\\ & =\underset{x\to 1^{-}}{lim}\frac{1}{\sqrt{(1+x)(1-k^2{x}^2)}}=\frac{1}{\sqrt{2(1-k^2)}},q=\frac{1}{2}<1\\ & \therefore {\int }_0^1\frac{1}{\sqrt{(1-x^2)(1-k^2{x}^2)}}dx\text{ 收敘. }(\text{ 极限审敛法2 })\end{array}$

例9

判别反常积分 ${\int }_0^1\frac{\sin \frac{1}{x}}{\sqrt{x}}dx$ 的收敛性. 解 $\sin \frac{1}{x}$ 在0的右半邻域内无界 $\therefore x=0$ 是瑕点 $\because |\frac{\sin \frac{1}{x}}{\sqrt{x}}|\le \frac{1}{\sqrt{x}},$ 而 ${\int }_0^1\frac{dx}{\sqrt{x}}$ 收敛, $[\because q=\frac{1}{2}<1]$ $\therefore {\int }_0^1\frac{\sin \frac{1}{x}}{\sqrt{x}}dx$ 收敛 $(\text{ 比较审敛法2 })\therefore {\int }_0^1|\frac{\sin \frac{1}{x}}{\sqrt{x}}|dx$ 也收敛

例10

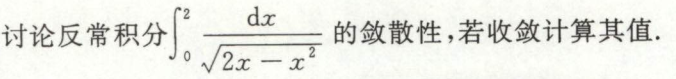
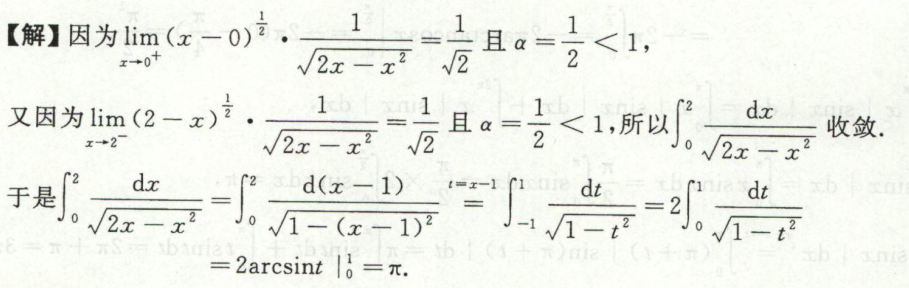
例11

首先是要审敛，要发现这是个反常积分。

这里有四种方法，换元法，分部积分法，分子有理化，1的代换。都可以做出来，亮瞎眼。

例12

对泊松型积分和$\mathrm{\Gamma }$函数的求解

例1

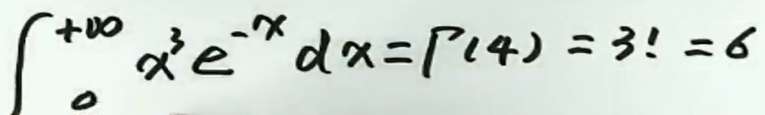
例2

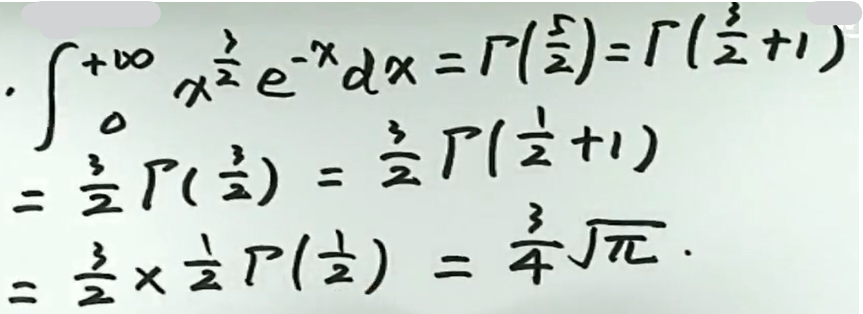
例3

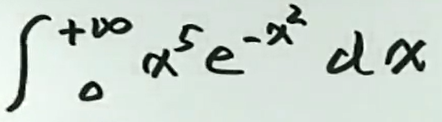
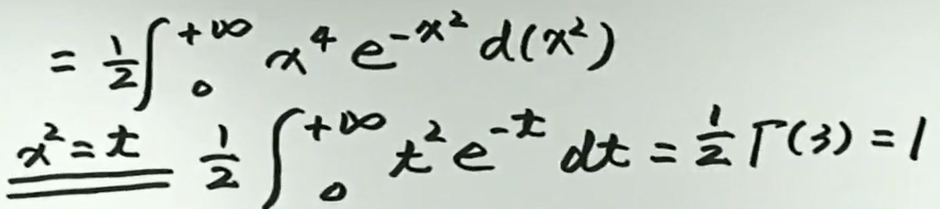
例4

求 $\mathrm{\Gamma }\left(\frac{7}{2}\right)$ 解 由递推公式得： $\begin{array}{rl}\mathrm{\Gamma }\left(\frac{7}{2}\right)& =\frac{5}{2}\cdot \mathrm{\Gamma }\left(\frac{5}{2}\right)\\ & =\frac{5}{2}\cdot \frac{3}{2}\cdot \mathrm{\Gamma }\left(\frac{3}{2}\right)\\ & =\frac{5}{2}\cdot \frac{3}{2}\cdot \frac{1}{2}\mathrm{\Gamma }\left(\frac{1}{2}\right)\\ & =\frac{5}{2}\cdot \frac{3}{2}\cdot \frac{1}{2}\sqrt{\pi }=\frac{15}{8}\sqrt{\pi }\end{array}$

例5

用$\mathrm{\Gamma }$函数表示积分 ${\int }_0^{+\mathrm{\infty }}{e}^{-x^4}dx$

解 ${\int }_0^{+\mathrm{\infty }}{e}^{-x^4}dx\stackrel{\text{令 }t=x^4}{=}{\int }_0^{+\mathrm{\infty }}{e}^{-t}\frac{1}{4}{t}^{-\frac{3}{4}}dt$ $=\frac{1}{4}{\int }_0^{+\mathrm{\infty }}{e}^{-t}{t}^{-\frac{3}{4}}dt$ $=\frac{1}{4}{\int }_0^{+\mathrm{\infty }}{e}^{-t}{t}^{\frac{1}{4}-1}dt$ $=\frac{1}{4}\mathrm{\Gamma }\left(\frac{1}{4}\right)$

例6