高等数学-一元积分学-定积分的应用
高等数学-一元积分学-定积分的应用
几何应用
面积
直角坐标系中\(L : y=f(x) \geqslant 0 \quad(a \leq x \leq b)\)
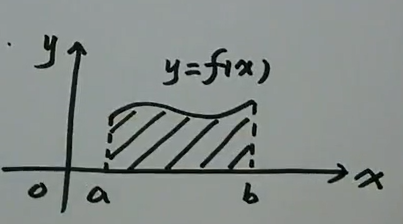
\(A=\int_{a}^{b} f(x) d x\)
极坐标系中\(L: r=r(\theta) \quad(\alpha \leq 0 \leq \beta)\)

取\([\theta,\theta+d \theta] \subset[\alpha, \beta]\), \(d A=\frac{1}{2} r^{2}(\theta) d \theta\) \(A=\frac{1}{2} \int_{\alpha}^{\beta} r^{2}(\theta) d \theta\)

\(A=\frac{1}{2} \int_{\alpha}^{\beta}\left[r_{2}^{2}(\theta)-r_{1}^{2}(\theta)\right] d \theta\)
旋转体表面积

取\([x, x+d x]<[a, b]\), \(d A=2 \pi | f(x) | \cdot d s\) \(2 \pi \cdot | f(x) | \cdot \sqrt{\left.1+f^{\prime} | x\right)} d x\) \(A=2 \pi \int_{a}^{b}|f(x)| \cdot \sqrt{1+f^{\prime}(x)} d x\)
体积
图形绕x轴旋转体积

取\([x, x+d x]<[a, b]\), \(d v=\pi f^{2} (x) \cdot d x\) \(V_{x}=\pi \int_{a}^{b} f^{2} (x) d x\)
图形绕y轴旋转体积

取\([x, x+d x]<[a, b]\), \(d v=2 \pi|x| \cdot|f(x)| \cdot d x\) \(V_{y}=2 \pi \int_{a}^{b}|x| \cdot|f(x)| \cdot d x\)
已知截面面积求体积
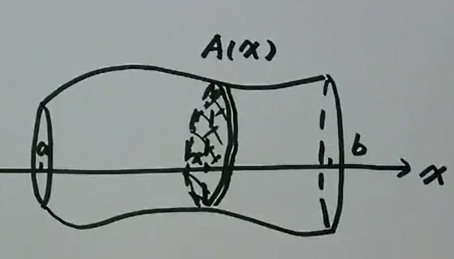
取\([x, x+d x]<[a, b]\), \(d v=A(x) d x\) \(v=\int_{a}^{b} A(x) d x\)
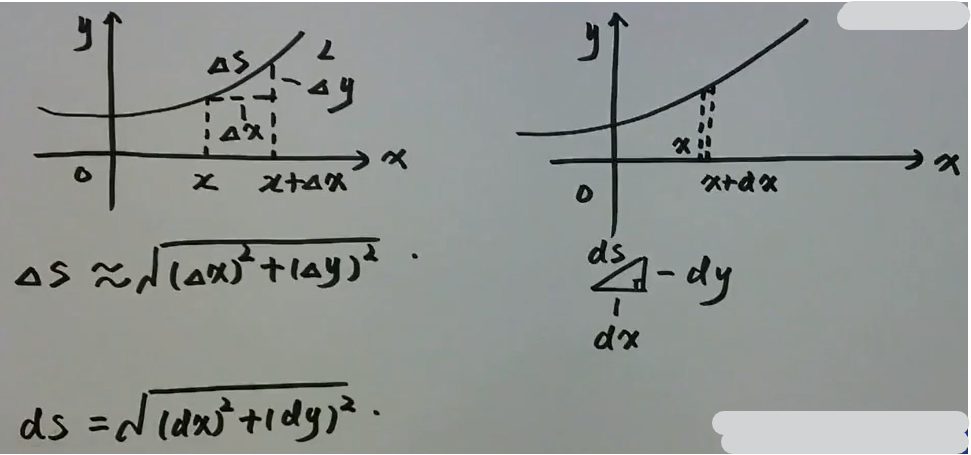
弧长
弧长部分可结合高等数学-一元微分学-应用-弧微分与曲率部分来看

直角坐标系\(L: y=f(x)(a \leq x \leq b)\)
取\([x, x+d x]<[a, b]\), \(d s=\sqrt{1+f^{\prime}(x)} d x\) \(l=\int_{a}^{b} \sqrt{1+f^{\prime 2}(x)} d x\)
参数方程\(\begin{array}{l}\left\{\begin{array}{ll}x=\varphi(t) \\ y=\psi(t)\end{array}\right. & (\alpha \leqslant t \leqslant \beta)\end{array}\)
取\([t, t+d t]<[\alpha , \beta]\), \(\begin{aligned} d s &=\sqrt{(d x)^{2}+\left( d y\right)^{2}}=\sqrt{\left(\frac{d x}{d t}\right)^{2}+\left(\frac{d y}{d t}\right)^{2}} d t \\ &=\sqrt{\varphi^{\prime}(t)+\psi^{\prime}(t)} d t \end{aligned}\) \(l=\int_{\alpha}^{\beta} \sqrt{\varphi^{\prime 2}(t)+\psi^{\prime 2} ( t)} d t\)
极坐标系\(L: r=r(\theta)\)
极坐标曲线 \(r=r(\theta), \alpha \leqslant \theta \leqslant \beta\) 的弧长(其中 \(r(\theta), r^{\prime}(\theta)\) 连续,且不同时为零) \[ s=\int_{a}^{\beta} \sqrt{r^{2}(\theta)+r^{\prime 2}(\theta)} \mathrm{d} \theta \]
圆\((a>0)\)
\(x^{2}+y^{2}=a^{2} \Leftrightarrow r=a\)
\(x^{2}+y^{2}=2 a x \Leftrightarrow(x-a)^{2}+y^{2}=a^{2}\)对应极坐标系\(x=2 a \cos \theta\)
\(x^{2}+y^{2}=2 a y \Leftrightarrow x^{2}+(y-a)^{2}=a^{2}\)对应极坐标系\(r=2 a \sin \theta\)
双扭线

\(\left(x^{2}+y^{2}\right)^{2}=a^{2}\left(x^{2}-y^{2}\right)\)对应极坐标系\(r^{2}=a^{2} \cos 2 \theta\)
摆线

\(L : \left\{\begin{array}{l}x=a(t-\sin t) \\ y=a(1-\cos t)\end{array} \quad(0 \leq t \leq 2 \pi)\right.\)
心形线
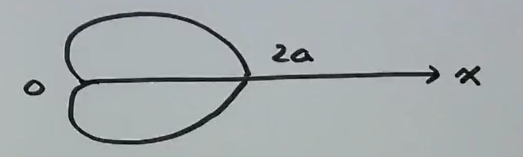
\(L: r=a(1+\cos \theta)\)