高等数学-向量代数与空间解析几何

这里先引进向量的概念,根据向量的线性运算建立空间坐标系,然后利用坐标讨论向量的运算；并介绍空间解析几何的有关内容。

在平面解析几何中,通过坐标法把平面上的点与一对有次序的数对应起来，把平面上的图形和方程对应起来,从而可以用代数方法来研究几何问题. 空间解析几何也是按照类似的方法建立起来的.通过坐标法把空间中的点与一对有次序的数对应起来，把空间里的图形和方程对应起来,从而可以用代数方法来研究几何问题.

向量及向量代数理论

向量的基本概念与定义（几何刻画）

向量/矢量：有大小、有方向的量。分为自由向量与非自由向量。数学中研究自由向量。z 向量的表示：一般用带方向的线段表示。一般记为\(\boldsymbol a, \vec{a}, \vec{AB}\)

自由向量：与起点位置无关的向量。数学研究自由向量（而速度等物理量，和位置有关，不属于自由向量）

向量相等：如果两个向量\(\vec{a}\)与\(\vec{b}\)大小相等、且方向相同，称这两个向量相等。

向量的模：向量的大小叫做向量的模。向量\(\vec{AB} , a\) 和 \(\vec{a}\) 的模依次记作 \(|\overrightarrow{A B}|,|\boldsymbol a|\) 和 \(|\vec{a}|\)

单位向量：模为1的向量称为单位向量。

向量的夹角：设有两个非零向置 \(a, b,\) 任取空间一点 \(O,\)作 \(\overline{O A}=a, \overline{O B}=b,\) 规定不超过 \(\pi\) 的 \(\angle A O B\) ( 设 \(\varphi=\angle A O B, 0 \leqslant \varphi \leqslant \pi)\) 称为向量 \(a\) 与 \(b\) 的夹角。记作 \(\hat{(\boldsymbol{a}, \boldsymbol{b})}\) 或 \(\hat{(\boldsymbol{b}, \boldsymbol{a})},\) 即 \(\hat{(\boldsymbol{a}, \boldsymbol{b})}=\varphi\)

向量共线/向量平行：若两个向量的起点放到一起时，当它们的终点和公共起点在一条直线上，称这两个向量共线。两平行向量一定共线，两向量共线也一定平行，两个概念等同。

向量共面：设有\(k(k\ge 3)\)个向量，当它们的起点放在一起时，如果k个终点和它们的公共起点在同一平面上，就称这k个向量共面。

而选取基矢，得到坐标系后，利用坐标表示这些概念的方法，在后文介绍。

向量的线性运算与性质（几何刻画）

此节介绍向量线性运算的概念、定义以及性质； 而选取基矢，确定坐标系后，利用坐标作向量的线性运算的方法，在后面介绍。

向量的加法

向量相加的三角形法则：设有两个向量 \(\boldsymbol{a}\) 与 \(\boldsymbol{b},\) 任取一点 \(A,\) 作 \(\overrightarrow{A B}=a,\) 月以 \(B\) 为起点, 作 \(\overrightarrow{B C}=b\), 连接 \(A C\), 那么向量 \(\overrightarrow{A C}=c\) 称为向母 \(a\) 与 \(b\) 的和，记作\(\vec{c}=\vec{a}+\vec{b}\)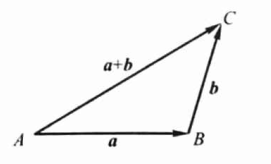

向量相加的平行四边形法则：当向量 \(\vec{a}\) 与 \(\vec{b}\) 不平行时,作 \(\overrightarrow{A B}=\vec{a}\),\(\overrightarrow{A D}=\boldsymbol{b},\) 以 \(A B, A D\) 为边作一平行四边形 \(A B C D,\) 连接对角线 \(A C\)即等于向量 \(\vec{a}\) 与 \(\vec{b}\) 的和 \(\vec{a}+\vec{b} .\)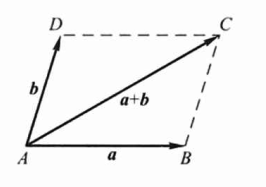

向量的减法

设\(\vec{ a}\) 为一向量,与 \(\vec{a}\) 的模相同而方向相反的向量叫做 \(\vec{a}\) 的负向量。记作 \(-\vec{a}\)

规定向量\(\vec{b}\) 与 \(\vec{a}\) 的差：\(b-a=b+(-a)\).则我们可以借助向量的加法来计算减法。

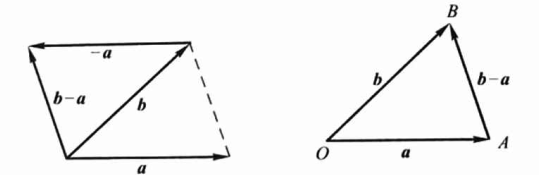
向量加减法性质

任给向量\(\vec{AB}\)及点O，有\(\overrightarrow{A B}=\overrightarrow{A O}+\overrightarrow{O B}=\overrightarrow{O B}-\overrightarrow{O A},\)

\(\vec{a}-\vec{a}=\vec{a}+(-\vec{a})=0\)

由三角形两边之和大于第三边，有\(|a+b| \leqslant|a|+|b|\)及\(|a-b| \leqslant|a|+|b|\)

向量与数的乘法（数乘）概念

向量\(\vec{a}\) 与实数 \(\lambda\) 的乘积记作 \(\lambda \vec{a},\) 规定 \(\lambda \vec{a}\) 是一个向量,它的模\(|\lambda a|=|\lambda||a|\)， 它的方向当 \(\lambda>0\) 时与 \(a\) 相同, 当 \(\lambda<0\) 时与 \(a\) 相反. 当 \(\lambda=0\) 时, \(|\lambda \vec{a}|=0,\) 即 \(\lambda \vec{a}\) 为零向量,这时它的方向可以是任意的.

特别的，当 \(\lambda=\pm 1\) 时,有\(1 \vec{a}=\vec{a},(-1) \vec{a}=-\vec{a}\)

向量数乘的性质

结合律

\(\lambda(\mu \vec{a})=\mu(\lambda \vec{a})=(\lambda \mu) \vec{a}\)

分配律

\((\lambda+\mu) \vec{a}=\lambda \vec{a}+\mu \vec{a}\) \(\lambda(\vec{a}+\vec{b})=\lambda \vec{a}+\lambda \vec{b}\)

\(\boldsymbol{a}=|\boldsymbol{a}| \boldsymbol{{e}_{n}}, \quad \frac{\boldsymbol{a}}{|\boldsymbol{a}|}= \boldsymbol{{e}_{n}}\)

向量平行的充分必要条件

设向量 \(\vec{a} \neq 0,\) 则向量 \(\vec{b}\) 平行于 \(\vec{a}\) 的充分必要条件是 :存在唯一的实数\(\lambda,\) 使 \(\vec{b}=\lambda \vec{a}\)

向量的坐标表示（代数刻画）

数轴上的点与向量坐标一一对应

给定一个点，一个方向及单位长度，就确定了一条数轴。

设点 O 及单位向量 \(\boldsymbol i\) 确定了数轴 Ox。 对于轴上任一点 P, 对应一个向\(\overrightarrow{OP}\)，根据向量平行的充分必要条件，必存在唯一的实数x，使得\(\overrightarrow{O P}=x \boldsymbol i\)，并知\(\vec{OP}\)和x一一对应。 即：点 \(P \longleftrightarrow\) 向量 \(\overrightarrow{O P}=x \boldsymbol i \longleftrightarrow\) 实数 \(x\) 即：轴上的点P与实数x有一一对应的关系，据此定义x为轴上点P的坐标。 则，轴上点P坐标为x\(\quad\Leftrightarrow \quad\overrightarrow{O P}=x \boldsymbol i\)

需要注意的是x既是点P的坐标，又是向量\(\vec{OP}\)的坐标，点和向量是两个不同的概念，上下文中要注意区分。

数轴（一维坐标系）

在1维数轴上，可以选定一个方向为数轴正向的矢量（向量），作为基本矢量/基矢。 比如\(\vec{AB} = (4-1)\vec{e} = 3\vec{e}\)，其中3称为\(\vec{AB}\)的坐标。 一般情况下，有\(\vec{AB} = (x_2-x_1)\vec{e}\)

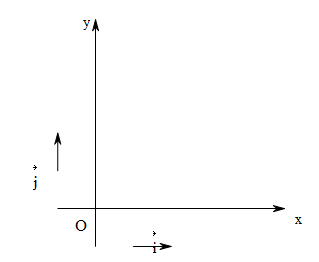
二维坐标系以及平面直角坐标系

在二维平面上，可以选定某原点O，以及两个不同方向/不共线/不平行的单位矢量\(\boldsymbol i, \boldsymbol j\)（基本矢量/单位向量），分别确定两条数轴。

根据向量的加法，平面内的任意向量\(\vec{AB}\)都可以平移到原点位置，并分解到基矢的两个数轴方向上$ = + \(； 根据[向量平行的充分必要条件](#向量平行的充分必要条件)有\) = _1 i, = _2 j \(, 则\) = _1 i + _2 j $ 即二维平面中的任何向量都可以由两个基矢线性表示。 \((\lambda_1, \lambda_2)\)称为平面向量\(\vec{AB}\)在以单位向量\(\boldsymbol i, \boldsymbol j\)确定的坐标轴（数轴）上的坐标。 二维平面中的所有向量对应的坐标，形成平面坐标系

特别的，可以以二维平面中的两个互相垂直的单位向量\(\boldsymbol i, \boldsymbol j\)确定坐标轴，来表示平面中的任意向量。此时平面中的所有向量的坐标称为平面直角坐标系。

一般情况下，在以单位向量\(\boldsymbol i, \boldsymbol j\)分别确定的坐标轴形成的平面坐标系中，若平面中两点\(A(x_1,y_1), B(x_2,y_2)\)，则平面向量\(\vec{AB} = \vec{A_1 B_1} + \vec{A_2 B_2} = (x_2 - x_1) \vec{i} + (y_2-y_1)\vec{j}\)，即将\(\vec{AB}\)的平移\((-x_1, -y_1)\)到原点位置，得平面向量\(AB\)的坐标\((x_2-x_1, y_2-y_1)\)。

需要注意的是平面中坐标为\((x,y)\)的点P，向量\(\vec{OP}\)的坐标也是\((x,y)\)，点和向量是两个不同的概念，上下文中要注意区分。

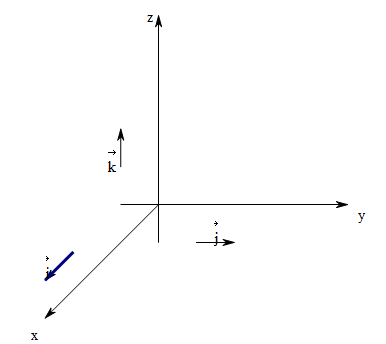
三维坐标系以及空间直角坐标系

在三维空间中，可以选定三个不共面的矢量（向量）\(\boldsymbol i , \boldsymbol j, \boldsymbol k\)，作为基本矢量/基矢，以这三个基本矢量，可以分别确定一条数轴。类比二维的情况，根据向量的线性运算（加法与数乘），空间中的任意向量都可用这三个基本矢量\(\boldsymbol i , \boldsymbol j, \boldsymbol k\)线性表示。 即\(\vec{AB} = \lambda_1 \boldsymbol i + \lambda_2 \boldsymbol j + \lambda_3 \boldsymbol k\)， 而\((\lambda_1, \lambda_2, \lambda_3)\)称为向量\(\vec{AB}\)在以单位向量\(\boldsymbol i , \boldsymbol j, \boldsymbol k\)确立的坐标轴（数轴）上的坐标。 三维空间中的所有向量对应的坐标，形成空间坐标系

特别的，可以以三维空间中的三个不共线的单位向量\(\boldsymbol i, \boldsymbol j\)确定坐标轴，来表示空间中的任意向量。此时空间中的所有向量的坐标，称为空间直角坐标系。

一般情况下，空间中的任意两点\(A(x_1,y_1,z_1), B(x_2,y_2,z_2)\),都可形成向量\(\vec{AB}\)。通过将向量平移\((-x_1,-y_1,-z_1)\)到原点，有\(\vec{AB} = \vec{A_1 B_1} + \vec{A_2 B_2} + \vec{A_3 B_3} = (x_2 - x_1) \vec{i} + (y_2-y_1)\vec{j} + (z_2-z_1)\vec{k}\)，得到向量的坐标表示\((x_2-x_1, y_2-y_1,z_2-z_1)\)

需要注意的是空间中坐标为\((x,y，z)\)的点P，向量\(\vec{OP}\)的坐标也是\((x,y,z)\)，点和向量是两个不同的概念，上下文中要注意区分。

向量的线性运算与性质（代数刻画，利用坐标）

设两个向量\(\boldsymbol{a}=\left(a_{x}, a_{y}, a_{z}\right), \boldsymbol{b}=\left(b_{x}, b_{y}, b_{z}\right)\),即\(a=a_{x} \boldsymbol i+a_y \boldsymbol j+a_{z} \boldsymbol k, b=b_{x} \boldsymbol i+b_{y} \boldsymbol j+b_{z} \boldsymbol k\)

向量的加法（利用坐标运算）

\(\boldsymbol{a}+\boldsymbol{b}=\left(a_{x}+b_{x}\right) \boldsymbol{i}+\left(\boldsymbol{a},+b_{y}\right) \boldsymbol{j}+\left(a_{z}+b_{z}\right) \boldsymbol{k}\) 即\(a+b=\left(a_{x}+b_{x}, a_{y}+b_{y}, a_{z}+b_{z}\right)\)

向量的减法（利用坐标运算）

\(\boldsymbol{a}-\boldsymbol{b}=\left(a_{x}-b_{x}\right) \boldsymbol{i}+\left(a_{y}-b_{y}\right) \boldsymbol{j}+\left(a_{z}-b_{z}\right) \boldsymbol{k}\)

即\(\boldsymbol{a}-\boldsymbol{b}=\left(a_{x}-b_{x}, a_{y}-b_{y},, a_{z}-b_{z}\right)\)

向量的数乘（利用坐标运算）

\(\lambda \boldsymbol{a}=\left(\lambda a_{x}\right) \boldsymbol{i}+\left(\lambda a_{y}\right) \boldsymbol{j}+\left(\lambda \boldsymbol{a}_{z}\right) \boldsymbol{k} \quad(\lambda\) 为实数 \()\)

即\(\lambda \boldsymbol{a}=\left(\lambda a_{x}, \lambda a_{y}, \lambda a_{z}\right)\)

向量平行的充分必要条件（坐标表示）

当向量 \(\boldsymbol a \neq \boldsymbol 0\) 时，向量 \(\boldsymbol{b} / / \boldsymbol{a}\) 相当于 \(\boldsymbol{b}=\lambda \boldsymbol{a},\) 坐标表示式为\(\left(b_{x}, b_y, b_{z}\right)=\lambda\left(a_{x}, a_{y}, a_{z}\right)\)，即坐标对应成比例：\(\frac{b_{x}}{a_{x}}=\frac{b_{y}}{a_{y}}=\frac{b_{z}}{a_{z}}\)

向量的基本概念的坐标表示（代数刻画）

向量如下基本概念的定义在前面已有介绍：向量的基本概念与定义（几何刻画）

向量的模

向量的模：向量的大小称为向量的模。 则向量端点之间的距离就是向量的模。 设有点 \(A\left(x_{1}, y_{1}, z_{1}\right)\) 和点 \(B\left(x_{2}, y_{2}, z_{2}\right),\) 则点 \(A\) 与点 \(B\) 间的距离 \(|A B|\) 就是向量\(\overrightarrow{A B}\) 的模。 向量\(\begin{aligned} \overrightarrow{A B} &=\overrightarrow{O B}-\overrightarrow{O A}=\left(x_{2}, y_{2}, z_{2}\right)-\left(x_{1}, y_{1}, z_{1}\right) \\ &=\left(x_{2}-x_{1}, y_{2}-y_{1}, z_{2}-z_{1}\right) \end{aligned}\) A 、B 两点间的距离/向量\(\vec{AB}\)的模\(|A B|=|\overrightarrow{A B}|=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}+\left(z_{2}-z_{1}\right)^{2}}\)

单位向量

设直角坐标系中的向量\(\vec{a}=(a_1,a_2,a_3)\)

则与\(\vec{a}\)同方向的单位向量为\(\vec{a}^\circ = \frac{\vec{a}}{|\vec{a}|} = \left\{\frac{a_1}{\sqrt{a_1^2+b_1^2+c_1^2}},\frac{b_1}{\sqrt{a_1^2+b_1^2+c_1^2}}, \frac{c_1}{\sqrt{a_1^2+b_1^2+c_1^2}}\right\}\)

方向角

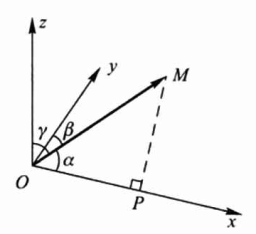
方向角：向量\(\vec{r}= \vec{OM}=(a_1,b_1,c_1)\)与x,y,z轴正向的夹角，一般记为\(\alpha,\beta,\gamma\).

方向余弦

\(\cos \alpha=\frac{a_1}{|O M|}=\frac{a_1}{|r|} = \frac{a_1}{\sqrt{a_1^2+b_1^2+c_1^2}}\)

\(\cos \beta=\frac{a_2}{|r|} = \frac{b_1}{\sqrt{a_1^2+b_1^2+c_1^2}}\)

\(\cos \gamma=\frac{a_3}{|r|} = \frac{c_1}{\sqrt{a_1^2+b_1^2+c_1^2}}\)

\(\cos^2 \alpha + \cos^2 \beta + \cos^2 \gamma = 1\)

\(\vec{a}^\circ = \frac{\vec{a}}{|\vec{a}|} = \{\cos \alpha, \cos \beta, \cos \gamma\}\)

向量的投影

点M在数轴u上的投影：过点M作与u轴垂直的平面交u轴于点M‘，则点M’称作点M在u轴上的投影。

向量\(\vec{r}= \vec{OM}\)在数轴u上的投影：过点M作与u轴垂直的平面交u轴于点M‘，则\(\vec{OM^\prime}\)称为向量\(\vec{r}\)在u轴上的分向量，设\(\vec{OM^\prime} = \lambda boldsymbol e\)，则\(\lambda\)称为向量\(\vec{r}= \vec{OM}\)在数轴u上的投影，记作\(\operatorname{Prj}_{u} \boldsymbol r\)或者\((\boldsymbol r)_u\)

直角坐标系中，设向量\(\vec{a} = (a_x,a_y,a_z)\)，则\(a_x,a_y,a_z\)恰好就是\(\vec{a}\)在三条坐标上的投影。

投影的性质： \(\operatorname{Prj}_{u} \boldsymbol a=|\boldsymbol a| \cos \varphi\) \(\operatorname{Prj}_{u}(\boldsymbol{a}+\boldsymbol{b})=\operatorname{Prj}_{u} \boldsymbol{a}+\operatorname{Prj}_{u} \boldsymbol{b}\) \(\operatorname{Prj}_{u}(\lambda \boldsymbol{a})=\lambda \operatorname{Prj}_{u} \boldsymbol{a}\)

向量的数量积、向量积与混合积

数量积\(\vec{a} \cdot \vec{b}\)

数量积的结果是个标量。

数量积定义（几何刻画）：

\(\vec{a} \cdot \vec{b}=|\vec{a}| \cdot |\vec{b}| \cos \hat{(\vec{a},\vec{b})}\)

\(\vec{a} \cdot \vec{b}=|\vec{a}| \operatorname{Prj}_{\vec{a}} \vec{b}\)

\(\vec{a} \cdot \vec{b}=|\vec{b}| \operatorname{Prj}_{\vec{b}} \vec{a}\)

意义：是其中一个向量与另一个向量在此方向投影的乘积的大小。

性质：

\(\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}\)

\((\vec{a}+\vec{b}) \cdot \vec{c}=\vec{a} \cdot \vec{c}+\vec{b} \cdot \vec{c}\)

\((\lambda \vec{a}) \cdot \vec{b}=\lambda(\vec{a} \cdot \vec{b}), \lambda\) 为数.

\(\vec{a} \cdot \vec{a}=|\vec{a}|^2\)

若\(\vec{a} \cdot \vec{a}=0 \Leftrightarrow \vec{a} = \vec{0}\)

若\(\vec{a} \cdot \vec{b}=0 \Leftrightarrow \vec{a} \perp \vec{b}\)

坐标表示（直角坐标系中的代数刻画）：

\(\boldsymbol a \cdot \boldsymbol b=\left(a_{x} \boldsymbol i+a_y \boldsymbol j+a_{z} \boldsymbol k\right) \cdot\left(b_{x} \boldsymbol i+b_u \boldsymbol j+b_{z} \boldsymbol k\right)=a_{x} b_{x}+a_{y} b_{y}+a_{z} b_{z}\)

向量积\(\vec{a} \times \vec{b}\)

向量积的结果是个向量。

向量积定义（几何刻画）：

向量积的方向：通过右手准则确定，并与\(\vec{a}\)和\(\vec{b}\)都垂直。 向量积的大小：\(|\vec{a} \times \vec{b}|=|\vec{a}| \cdot |\vec{b}| \sin \hat{(\vec{a},\vec{b})}\)

意义：由两个向量决定另一个向量方向。

性质：

\(\vec{a} \times \vec{a}=\vec{0}\)

\(\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}\)

\(\vec{a} \times \vec{b} \perp \vec{a}, \vec{a} \times \vec{b} \perp \vec{b}\)

\((\vec{a}+\vec{b}) \times \vec{c}=\vec{a} \times \vec{c}+\vec{b} \times \vec{c}\)

\((\lambda \vec{a}) \times \vec{b}=\vec{a} \times(\lambda \vec{b})=\lambda(\vec{a} \times \vec{b})\)

若对于两个非零向量，\(\vec{a} \times \vec{b}=\vec{0} \Leftrightarrow \vec{a} // \vec{b}\) 或\(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\)

\(|\vec{a} \times \vec{b}| = |\vec{a}| \cdot |\vec{b}| \sin \hat{(\vec{a},\vec{b})} = 2 S_\triangle\)

坐标表示（直角坐标系中的代数刻画）：

\(\vec{a} \times \vec{b} =\left(a_{x} \boldsymbol i+a_{y} \boldsymbol j+a_{z} \boldsymbol k\right) \times\left(b_{x} \boldsymbol i+b_{y} \boldsymbol j+b_{z} \boldsymbol k\right)= \left|\begin{array} \vec{i} & \vec{j} & \vec{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{array}\right|\)

混合积\((\vec{a} \times \vec{b})\cdot \vec{c}\)

三个向量的混合积是个标量。

混合积定义（几何刻画）：

\([\vec{a} \vec{b} \vec{c}]=(\vec{a} \times \vec{b}) \cdot \vec{c}\)

意义：它的绝对值表示以\(\vec{a} , \vec{b} , \vec{c}\)为棱的平行六面体的体积。

坐标表示（代数刻画）：

\([\vec{a} \vec{b} \vec{c}]=(\vec{a} \times \vec{b})\cdot \vec{c}=\left|\begin{array}{lll}a_{x} & a_{y} & a_{z} \\ b_{x} & b_{y} & b_{z} \\ c_{x} & c_{y} & c_{z}\end{array}\right|\)

性质：

3个向量\(\vec{a} , \vec{b} , \vec{c}\)共面 \(\Leftrightarrow\) \([\vec{a} \vec{b} \vec{c}]=(\vec{a} \times \vec{b})\cdot \vec{c}=0\)

向量的几何应用：空间解析几何

空间解析几何中，任何曲面或曲线都可以看作是点的几何轨迹。

空间解析几何将图形看作是点的轨迹，如何由几何轨迹建立方程、如何根据方程研究几何图形，是研究的两个基本的问题。

空间曲面\(F(x,y,z) = 0\)

对于曲面S和方程\(F(x,y,z) = 0\)，若： 1）曲面上任何一点的坐标都满足方程 2）曲面外任何一点的坐标都不满足方程 称这个方程\(F(x,y,z) = 0\)是曲面S的方程，曲面S是方程\(F(x,y,z) = 0\)的图形。

特殊曲面

球面

球心在点 \(M_{0}\left(x_{0}, y_{0}, z_{0}\right),\) 半径为 \(R\)，设 \(M(x, y, z)\) 是球面上的任一点，则有\(\left|M_{0} M\right|=R\) 即\(\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}+\left(z-z_{0}\right)^{2}=R^{2}\)

一般的，三元二次方程\(A x^{2}+A y^{2}+A z^{2}+D x+E y+F z+G=0\)都可以通过配方法化为球的方程的标准形式。其特点是缺 xy, yz,zx 各项, 而且平方项系数相同。

柱面

\(F(x,y)= 0\)表示某平行于z轴的柱面。平面上任意一条平行于z轴的直线称为柱面的母线，xOy面上的\(F(x,y)= 0\)叫做柱面的准线。 \(F(y,z)= 0\)表示某平行于x轴的柱面。 \(F(x,z)= 0\)表示某平行于y轴的柱面。

不论没出现的那个坐标取何值，点都在对应的曲面上。

旋转曲面

对于曲线: \(\left\{\begin{array}{} f(x,y) = 0 \\ z=0\end{array}\right.\)

绕x轴旋转形成的曲面\(\Sigma_x\)为： \(f(x,\pm \sqrt{y^2+z^2}) = 0\)

绕y轴旋转形成的曲面\(\Sigma_y\)为： \(f(\pm \sqrt{x^2+z^2}, y)= 0\)

规律是：绕谁旋转，谁不变

二次曲面

与平面解析几何中规定的二次曲线相似，我们把三元二次方程\(F(x, y, z)=0\)所表示的曲面称作二次曲面，把平面称作一次曲面。

我们可以通过截痕法、伸缩变形的方法得到二次曲面的形状。

共有9种二次曲面。

其中三种： 这3种二次曲面是以二次曲线为准线的柱面：

椭圆柱面：\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) 双曲柱面：\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) 抛物柱面：$ x^{2}=a y$

剩余6种：

空间平面

空间平面可看作空间曲面的退化。

空间平面的点法式方程

设\(M_0(x_0,y_0,z_0) \in \pi\)平面，\(\vec{n} = {A,B,C} \perp \pi\)平面。 $M(x,y,z) =0 $ 所以\(\pi\)平面方程为：\(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)

空间平面的截距式方程

\(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 0\)

空间平面的一般式方程

\(Ax+By+Cy+D=0\)

两平面的夹角

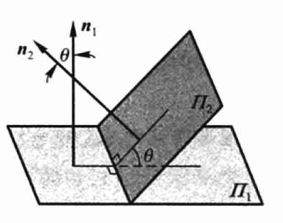
两平面的夹角等于两平面法向量的夹角，则：

\(\cos \theta=\frac{\vec{| n_1 \cdot \vec{n_2}|}}{|\vec{n_1}| \cdot| \vec{n_2}|}=\frac{\left|A_{1} A_{2}+B_{1} B_{2}+C_{1} C_{2}\right|}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}} \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}\)

从两向量垂直、平行的充分必要条件可推得： 平面\(\Pi_{1}, \Pi_{2}\) 互相垂直相当于 \(A_{1} A_{2}+B_{1} B_{2}+C_{1} C_{2}=0\) 平面\(\Pi_{1}, \Pi_{2}\) 互相平行或重合相当于 \(\frac{A_1}{A_{2}}=\frac{B_{1}}{B_{2}}=\frac{C_{1}}{C_{2}}\)

平面束方程

设直线 L 由如下方程组确定： \(\left\{\begin{array}{l}A_{1} x+B_{1} y+C_{1} z+D_{1}=0 \\ A_{2} x+B_{2} y+C_{2} z+D_{2}=0\end{array}\right.\) 其中系数 \(A_{1}, B_{1}, C_{1}\) 与 \(A_{2}, B_{2}, C_{2}\) 不成比例.

则三元一次方程组(其中 \(\lambda\) 为任意常数)： \(A_{1} x+B_{1} y+C_{1} z+D_{1}+\lambda\left(A_{2} x+B_{2} y+C_{2} z+D_{2}\right)=0\) 可表示过直线L的任意平面（除\(A_{2} x+B_{2} y+C_{2} z+D_{2}=0\)之外） 称为通过直线L的平面束方程。

空间曲面的切平面与法线

\(\Sigma: F(x,y,z)=0\)是空间曲面， \(M_0(x_0,y_0,z_0) \in \Sigma\)曲面， \(M_0\)处切平面的一个法向量为\(\vec{n} = \{F_x^\prime, F_y^\prime, F_z^\prime\}|_{M_0}\)

根据\(M_0\)和\(\vec{n}\)可写出曲面的切平面的点法式方程。 根据\(M_0\)和\(\vec{n}\)可写出曲面的法线的点向式方程。

空间曲线

空间曲线的表达形式

空间曲线的一般式方程

\(\left\{\begin{array}{} F(x,y,z) = 0 \\ G(x,y,z) = 0 \end{array}\right.\)

空间曲线的参数式方程

\(\left\{\begin{array}{} x=x(t) \\ y=y(t) \\ z=z(t) \end{array}\right.\)

空间曲线在坐标面上的投影

由空间曲线的一般式消去其中一元后（如果可以消去的话，比如消去z），得：\(H(x, y)=0\) 由前面已知，这是一个柱面，称为曲线关于平面xOy的投影柱面，再令z=0， 即得到空间曲线在xOy面的投影（方程）： \(\left\{\begin{array}{l}H(x, y)=0 \\ z=0\end{array}\right.\)

后面重积分章节，用投影法算三重积分可能会用到。

空间直线

空间直线可看作是空间曲线的退化。

空间直线的点向式方程

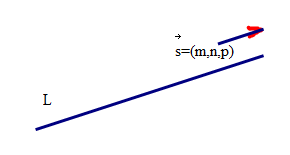
已知\(M_0 \in L, \vec{s} = \{m,n,p\} // L\)

\(\forall M(x,y,z) \in L \Leftrightarrow \vec{M_0 M} // \vec{s}\)，则L：\(\frac{x-x_0}{m} = \frac{y-y_0}{n} = \frac{z-z_0}{p}\)

当 m、n 和 p 中有一个为0,例如 m = 0, 而 n 与 p不等于0 时,这方程组应理解为 \(\left\{\begin{array}{l}x-x_{0}=0 \\ \frac{y-y_{0}}{n}=\frac{z-z_{0}}{p}\end{array}\right.\)

空间直线的参数式方程

令\(\frac{x-x_0}{m} = \frac{y-y_0}{n} = \frac{z-z_0}{p} = t\) 则L：\(\left\{\begin{array}{} x=x_0 +mt \\ y=y_0 + nt \\ z=z_0 + pt \end{array}\right.\)

空间直线的一般式方程

空间直线可看作是两个空间平面的交线。

则L：\(\left\{\begin{array}{} A_1 x + B_1 y + C_1 z + D_1 = 0 \\ A_2 x + B_2 y + C_2 z + D_2 = 0 \end{array}\right.\)

两空间直线的夹角

两直线的方向向量的夹角(通常指锐角或直角) 叫做两直线的夹角.

\(\cos \varphi= \frac{| \vec{s_1} \cdot \vec{s_2} |}{| \vec{s_1}| \cdot |\vec{s_2} |}=\frac{\left|m_{1} m_{2}+n_{1} n_{2}+p_{1} p_{2}\right|}{\sqrt{m_{1}^{2}+n_{1}^{2}+p_{1}^{2}} \sqrt{m_{2}^{2}+n_{2}^{2}+p_{2}^{2}}}\)

直线与平面的夹角

当直线与平面不垂直时，直线与它在平面上的投影直线的夹角为\(\varphi\left(0 \leqslant \varphi<\frac{\pi}{2}\right)\)，称为直线与平面的夹角。 当直线与平面垂直时，规定直线与平面的夹角为\(\frac{\pi}{2}\)

设直线的方向向量为 \(\vec{s}=(m, n, p)\),平面的法线向量为 \(\vec{n}=(A, B, C),\) 直线与平面的夹角为 \(\varphi=\left|\frac{\pi}{2}-\hat{(\boldsymbol s, \boldsymbol n)}\right|,\) 因此（当\(\varphi < \frac{\pi}{2}\)时）： \(\sin \varphi=|\cos \hat{(\boldsymbol s, \boldsymbol{n})}|=\frac{\left|A m+B n+C p\right|}{\sqrt{A^{2}+B^{2}+C^{2}} \sqrt{m^{2}+n^{2}+p^{2}}}\) 当直线与平面平行时（即当\(\varphi = 0\)时），直线与平面的法向量垂直: \(A m+B n+C p = 0\) 当至直线与平面垂直时（即当\(\varphi = \frac{\pi}{2}\)时），直线与平面的法向量平行： \(\frac{A}{m}=\frac{B}{n}=\frac{C}{p}\)

空间曲线的切线与法平面

根据空间曲线的参数式方程： \(\left\{\begin{array}{} x=x(t) \\ y=y(t) \\ z=z(t) \end{array}\right.\) 取\(t = t_0 \Rightarrow \text{切点}M_0(x_0, y_0, z_0)\) 切点\(M_0\)处的切向量\(\vec{T} = \{x^\prime(t_0), y^\prime(t_0), z^\prime(t_0)\}\) 则可以写出空间曲线的切线的点向式方程， 也可以写出空间曲线的法平面的点法式方程。

根据空间曲线的一般式方程： \(\left\{\begin{array}{} F(x,y,z) = 0 \\ G(x,y,z) = 0 \end{array}\right.\) 取\(M_0(x_0,y_0,z_0) \in \text{曲线} L\) 设\(\vec{n_1},\vec{n_2}\)分别是\(M_0\)处两个曲面$ F(x,y,z) = 0 , G(x,y,z) = 0\(的切平面的法向量，则\) = = { F_x^, F_y^, F_z^} { G_x^, G_y^, G_z^} $ 则可以写出空间曲线的切线的点向式方程， 也可以写出空间曲线的法平面的点法式方程。

距离

两点间的距离

设\(A(x_1,y_1,z_1), B(x_2,y_2,z_2)\) 则两点间的距离\(d=\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2}\)

点到平面的距离

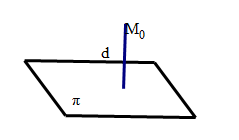
\(\pi \text{平面:} Ax+By+Cz+D=0,M_0(x_0,y_0,z_0) \notin \pi\) 则点\(M_0\)到\(\pi\)平面的距离\(d=\frac{|A x_0 + B y_0 + C z_0 + D|}{\sqrt{A^2+B^2+C^2}}\)

平行平面之间的距离

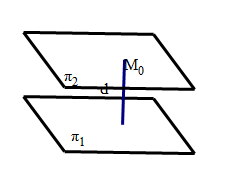
\(\pi_1 \text{平面:} Ax+By+Cz+D_1=0\) \(\pi_2 \text{平面:} Ax+By+Cz+D_2=0\)

取\(\forall M_0(x_0,y_0,z_0) \in \pi_2\)，则\(A x_0 + B y_0 + C z_0 + D_2 = 0\) 则\(M_0\)到平面\(\pi_1\)的距离就是两平面间的距离。 \(d=\frac{|A x_0 + B y_0 + C z_0 + D_1|}{\sqrt{A^2+B^2+C^2}}=\frac{|D_1 - D_2|}{\sqrt{A^2+B^2+C^2}}\)

点到直线的距离

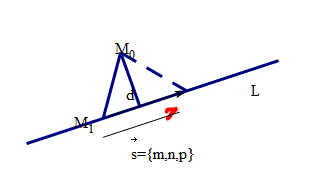
设\(M_0(x_0,y_0,z_0), M_1(x,y,z)\) 则有\(|\vec{M_1 M_0} \times \vec{s} | = 2 S_\triangle\) 又有\(|\vec{s}| \cdot d = 2 S_\triangle\) 则\(|\vec{s}| \cdot d =|\vec{M_1 M_0} \times \vec{s} |\) 则点\(M_0\)到直线L的距离\(d = \frac{|\vec{M_1 M_0} \times \vec{s} |}{|\vec{s}|}\)

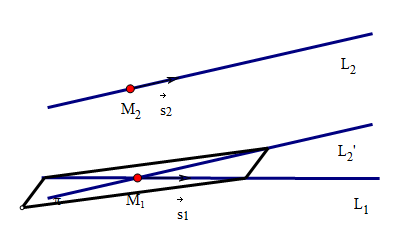
异面直线间的距离

1）准备工作： 在直线\(L_1\)上找任意一点\(M_1(x_1,y_1,z_1)\)，找直线\(L_1\)的一个方向向量\(\vec{s_1} = \{m_1,n_1,p_1\}\)。 在直线\(L_2\)上找任意一点\(M_2(x_2,y_2,z_2)\)，找直线\(L_2\)的一个方向向量\(\vec{s_2} = \{m_2,n_2,p_2\}\)。

2）确认两直线异面 \(L_1,L_2\)共面\(\Leftrightarrow \vec{s_1} \times \vec{s_2} \perp \vec{M_1 M_2} \Leftrightarrow (\vec{s_1} \times \vec{s_2}) \cdot \vec{M_1 M_2} = 0\) \(L_1,L_2\)异面\(\Leftrightarrow (\vec{s_1} \times \vec{s_2}) \cdot \vec{M_1 M_2} \neq 0\)

3）转化为求点到直线之间的距离 过点\(M_1\)作\(L_2^\prime // L_2\)，则\(L_1,L_2^\prime\)在一个平面\(\pi\)上 $M_1 \(平面，\) = \(，则可以确定平面\)$ 求异面直线间的距离转化为求点\(M_2\)到平面\(\pi\)的距离。