高等数学-基础概念-函数与极限习题
高等数学-基础概念-函数与极限习题
首先判断未定式类型,使用对应的方法 无法根据未定式求解时,考虑根据定义来做,或者夹逼定理,泰勒展开等 对于含有绝对值的式子求极限,需要分类讨论
根据未定式的形式求极限
\(\frac{0}{0}\)型、\(\frac{\infty}{\infty}\)型
等价无穷小求极限
例1
\(\lim _{x \rightarrow 0} \frac{e^{x}-e^{\ln (1+x)}}{x \arcsin 2 x}\)=?
答:
\(\frac{e^{x}-e^{\ln (1+x)}}{x+0} \frac{e^{x}}{x \arcsin 2 x}=\lim _{x \rightarrow 0} e^{\ln (1+x)} \cdot \frac{e^{x-\ln (1+x)}-1}{2 x^{2}}=\lim _{x \rightarrow 0} \frac{e^{x-\ln (1+x)}-1}{2 x^{2}}\) \(=\lim _{x \rightarrow 0} \frac{x-\ln (1+x)}{2 x^{2}}=\lim _{x \rightarrow 0} \frac{1-\frac{1}{1+x}}{4 x}=\frac{1}{4}\)
例2

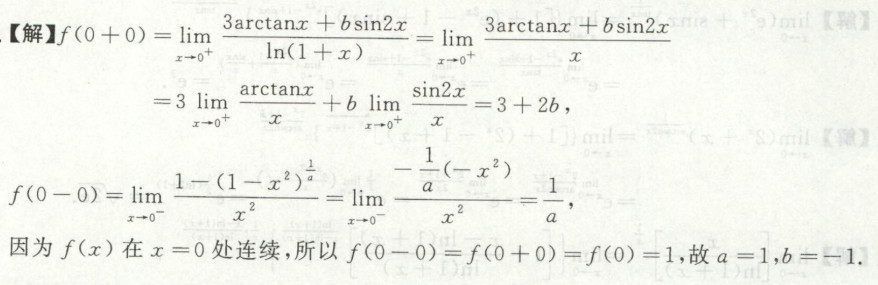
例3
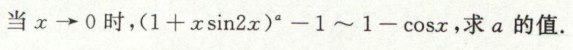
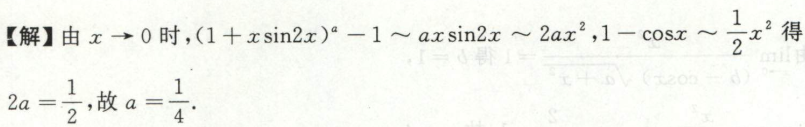
例4

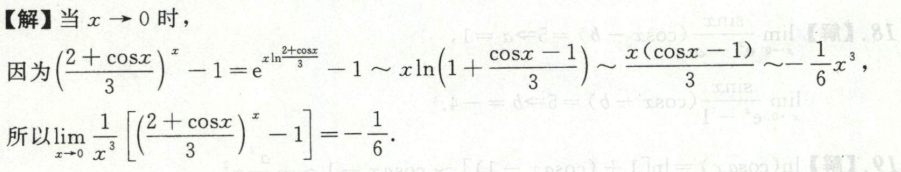
例5

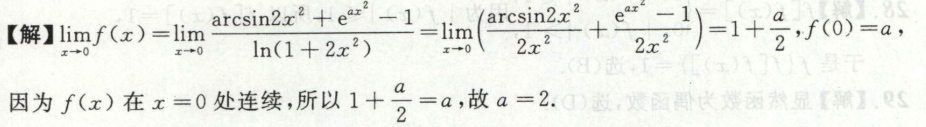
例6
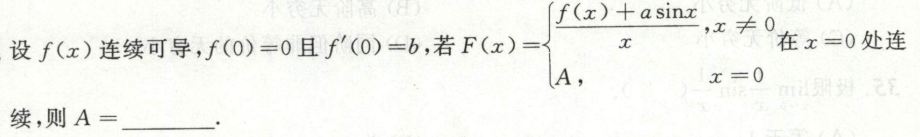

例7

这里使用等价无穷小,也可以使用和差化积+泰勒展开
例8
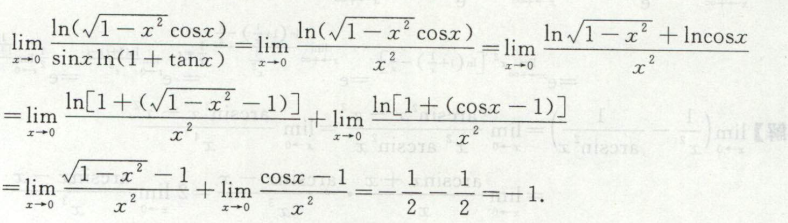
例9
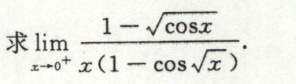

根式有理化或因式分解求极限
目的是尽可能的消去0或无穷因子,再用极限运算法则或连续函数极限的求法。
例1

例2
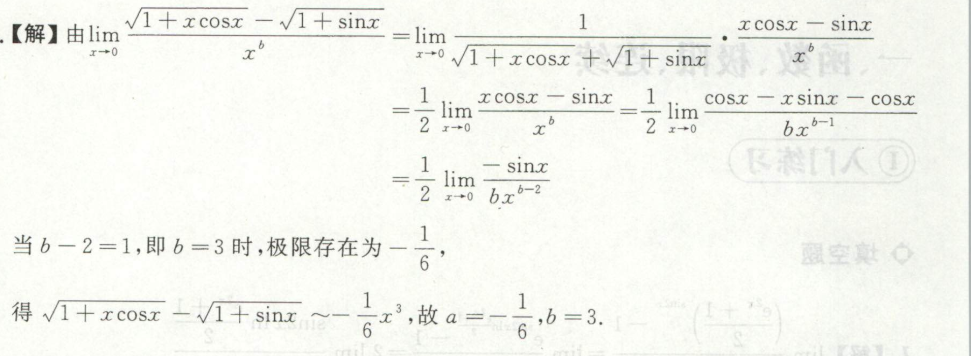
例3
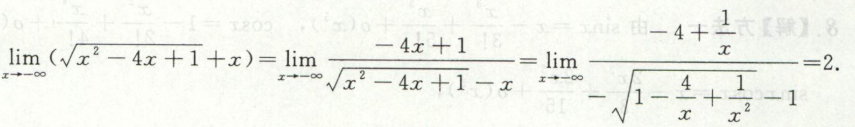
例3

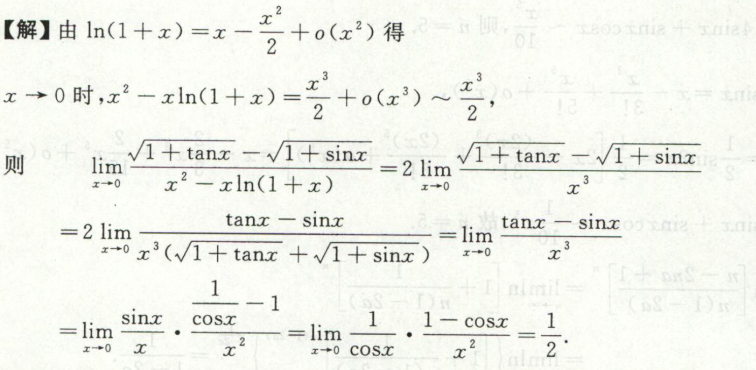
例4

例5
方法1根式有理化,方法2等价无穷小替换

例6
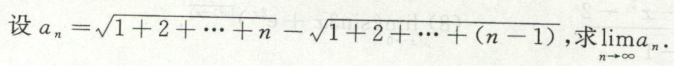
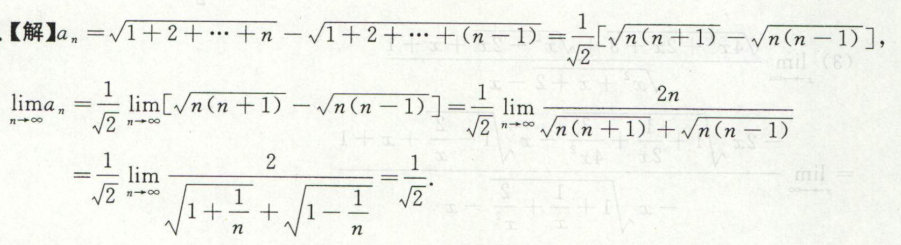
例7

洛必达法则求极限
例1
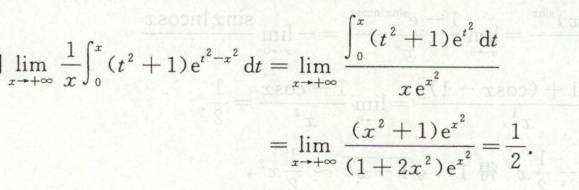
变量替换求极限
使用洛必达法则运算后,若式子反而比原来更复杂,应想到用变量替换。
例1


例2
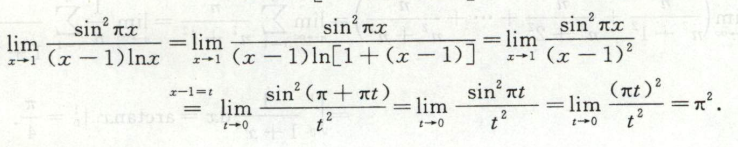
例3
本题用等价无穷小+变量替换

直接凑成或者添加因子凑成两个极限的积或和
例1

例2


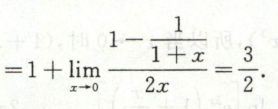
解此题还有一种方法见泰勒公式求极限的例1
例3

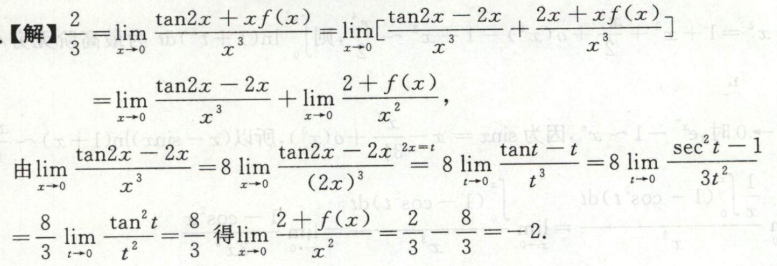
例4

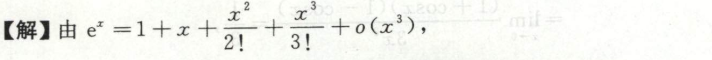
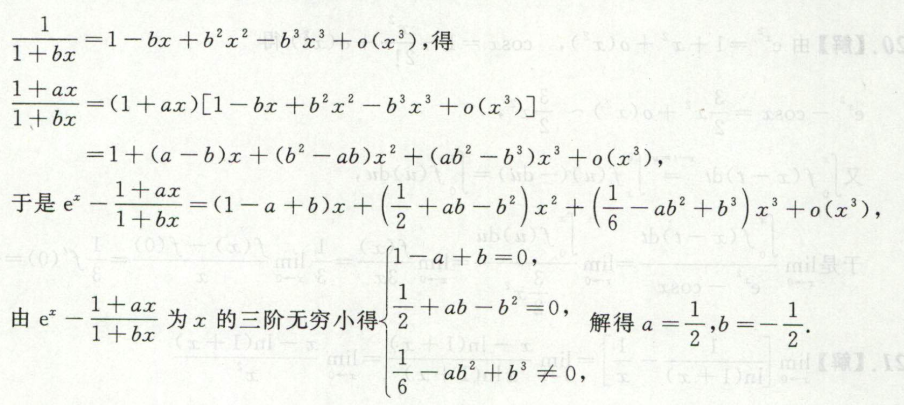
例5

此题也可对sin部分直接做等价无穷小代换
例6
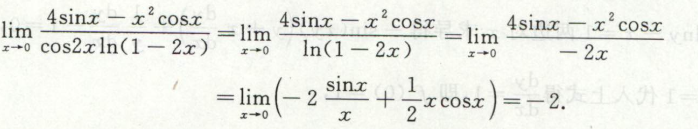
例7
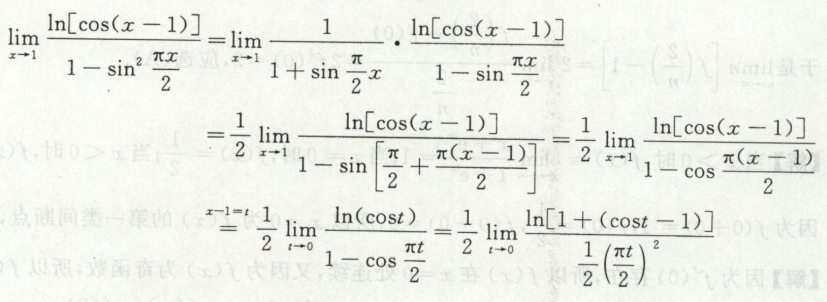
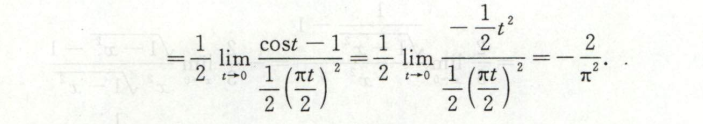
这道题先凑成两个极限的积,然后多次使用等价无穷小替换
例8
凑因子+洛必达+分子有理化
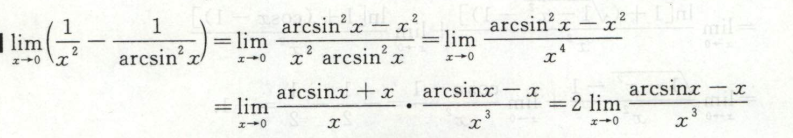
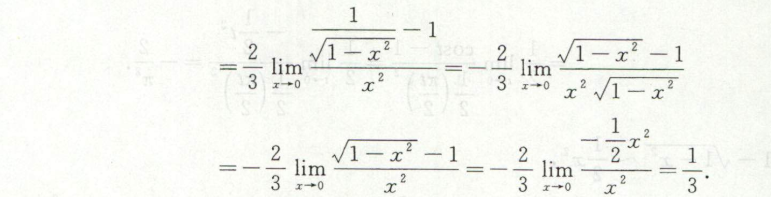
例9
凑因子+等价无穷小
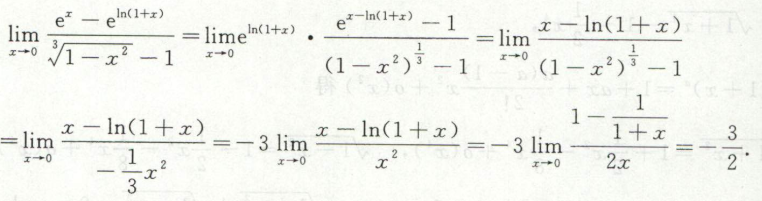
例10

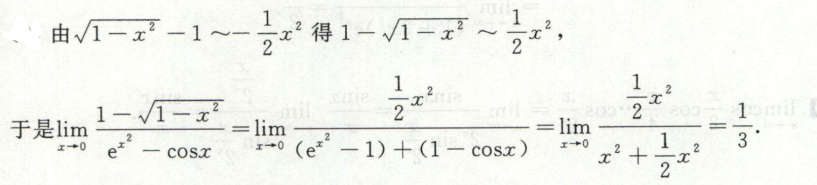
注意这里分母凑成两项的和,原式的倒数可以拆成两项使用等价无穷小替换,所以这里的分母也可以使用等价无穷小替换
例11
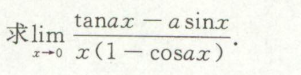

这道题是凑因子+泰勒展开
提因子留常数加无穷小量
例1

分子分母同除以因子求极限

化为对数形式
例1
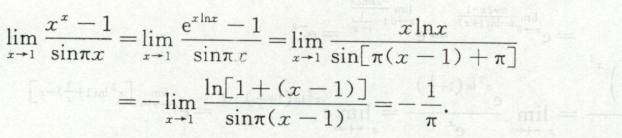
例2
化为对数形式+等价无穷小替换

\(\infty - \infty\)型求极限
通分求极限
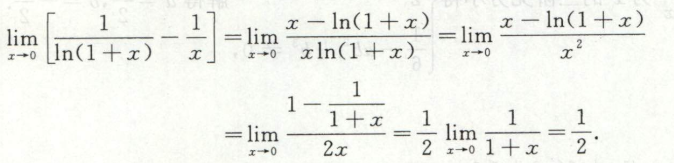
提因子变量替换求极限

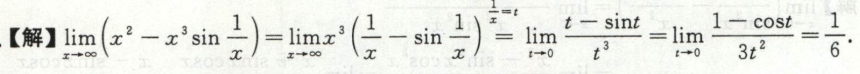
\(0\cdot \infty\)型求极限
变量替换
例1
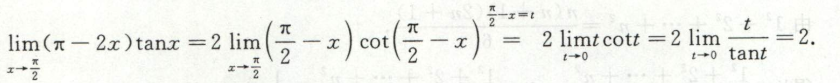
\(1^\infty\)型、\(0^0\)型、\(\infty^0\)型求极限
凑自然对数e求极限
例1

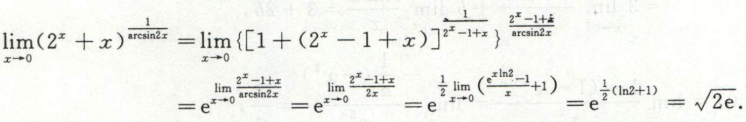
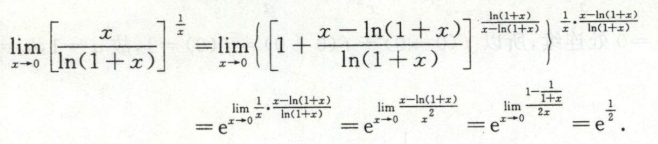
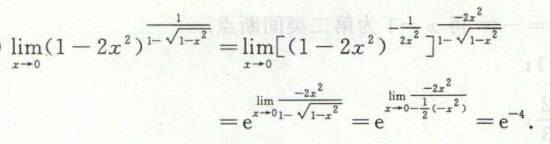





例2


例3
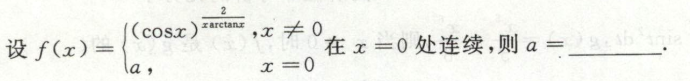
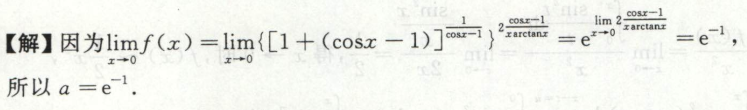
例4

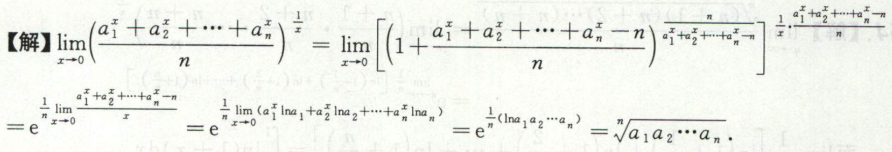
例5

例6

化为对数形式求极限
例1
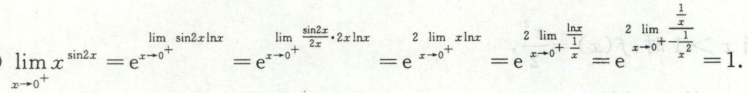
例2


例3

注意这里将分子化为了对数形式,而没有使用e的定义
例4

例5
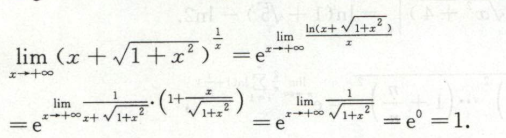
例6


例7

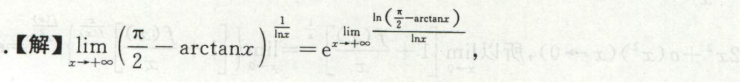

例8
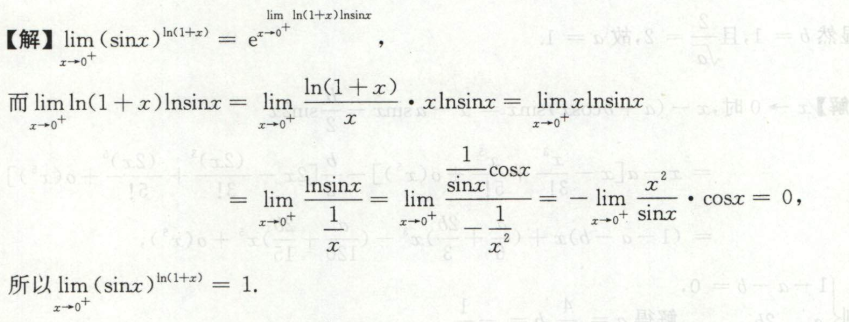
未定式求极限解不出时
根据相关定义求极限
根据导数定义求极限
例1
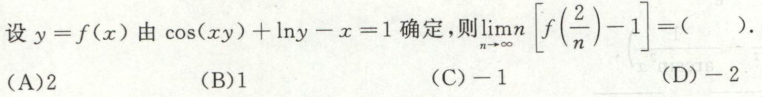

根据定积分定义求极限
(分子齐,分母不齐 )或者(分母齐,分子不齐)用夹逼定理。
分子分母都齐次用积分。
例1

例2


例3

根据恒等变换求极限
例1
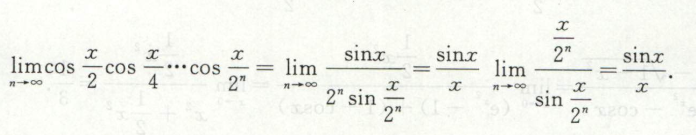
夹逼定理求极限
(分子齐,分母不齐 )或者(分母齐,分子不齐)用夹逼定理。
分子分母都齐次用积分。
例1
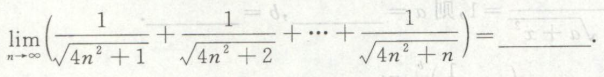

例2


例3

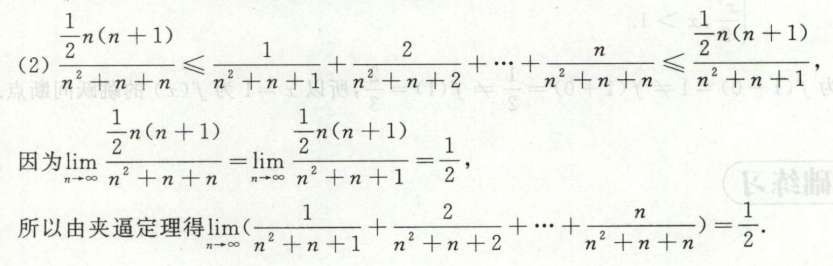
例4
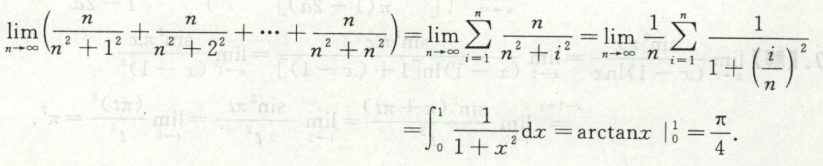
例5
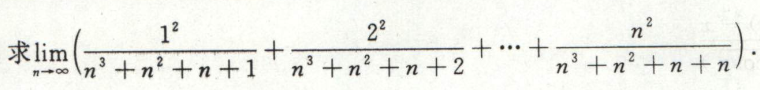
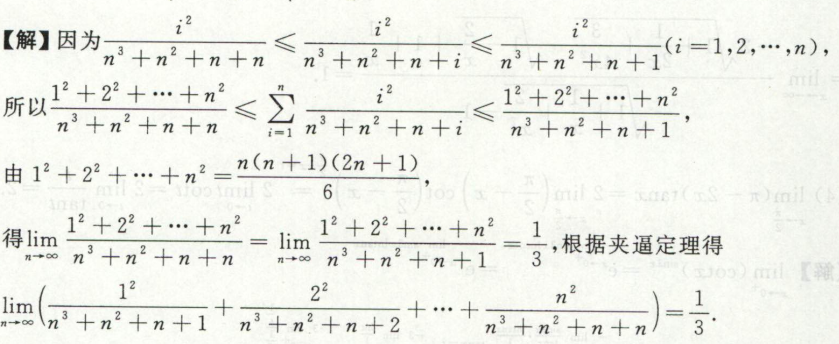
例6
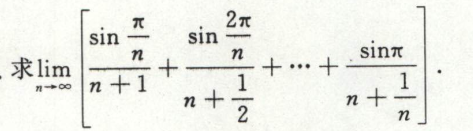

例7
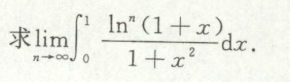
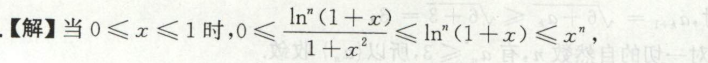
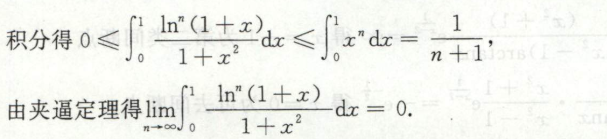
泰勒展开求极限
例1

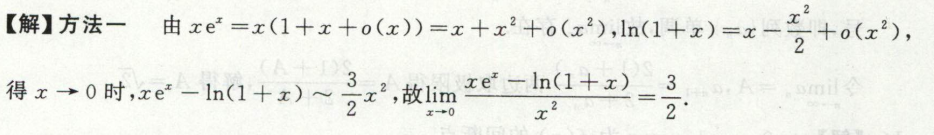
例2


例3



例4


例5

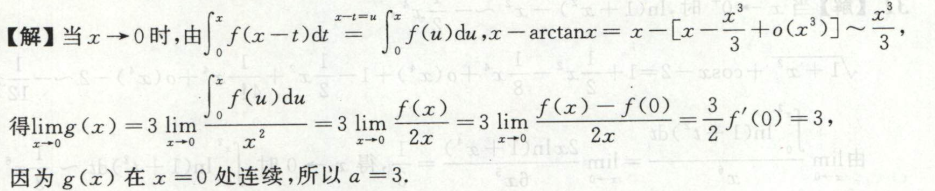
例6

可以使用泰勒展开+等价无穷小替换的方法:

也可以分母有理化+等价无穷小替换
例6
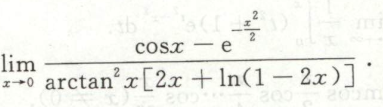

例7


例8
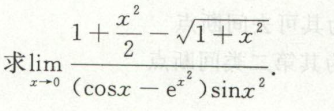
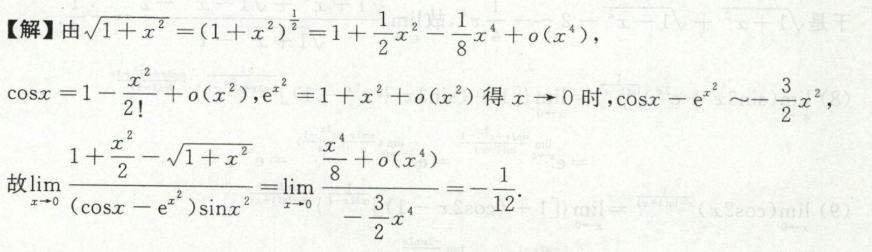
例9
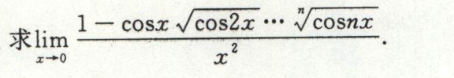
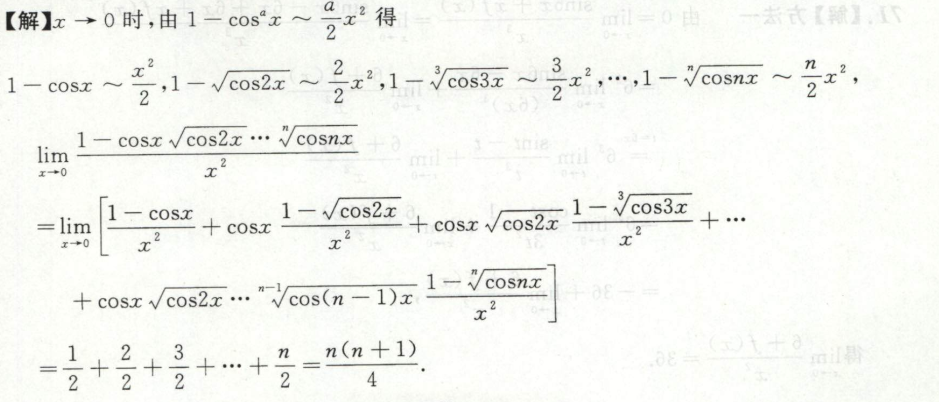
例10


本题也可以对分子使用和差化积公式+等价无穷小替换来做
例11


例12

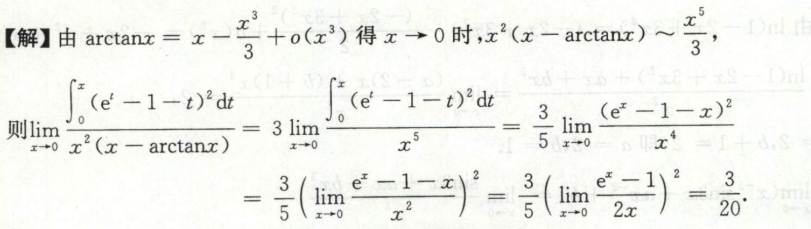
带绝对值式子求极限
例1


微分中值定理求极限
例1
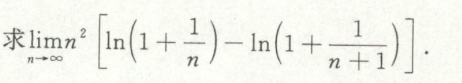
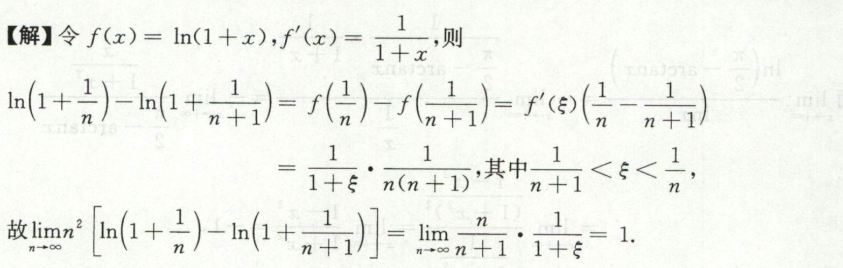
根据数列求极限
例1
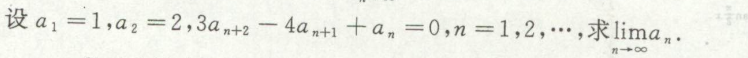
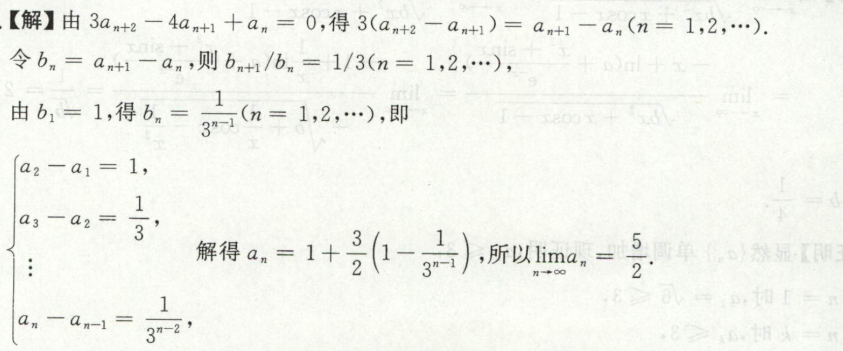
已知极限求其他
已知极限求参数
例1
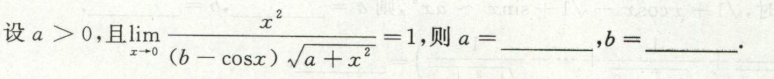

例2
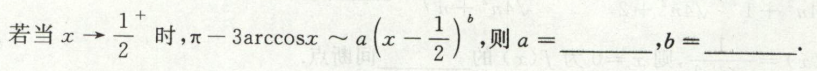
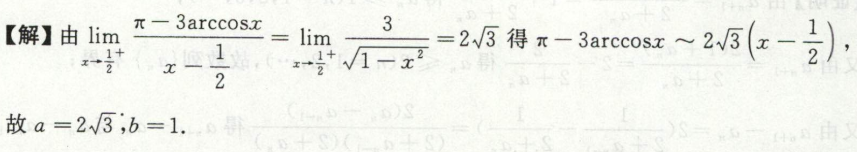
例3
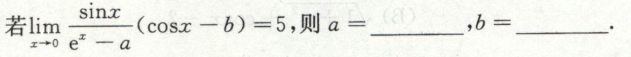

例4


例4


例5
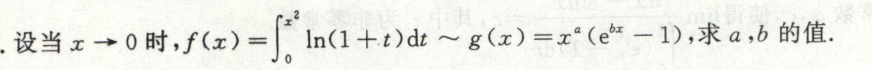
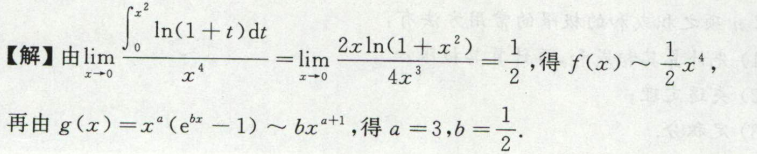
例6
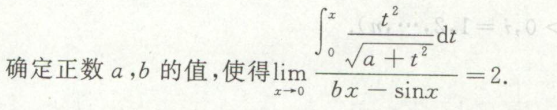
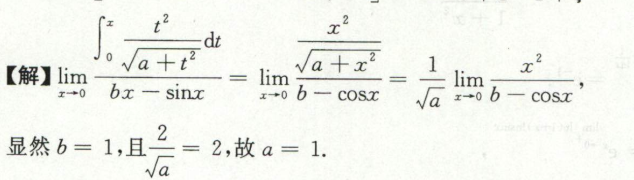
例7
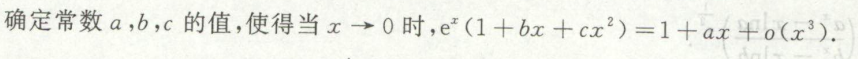

例8
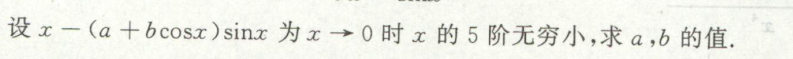

例9
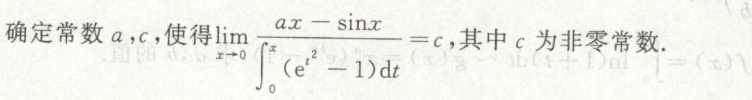
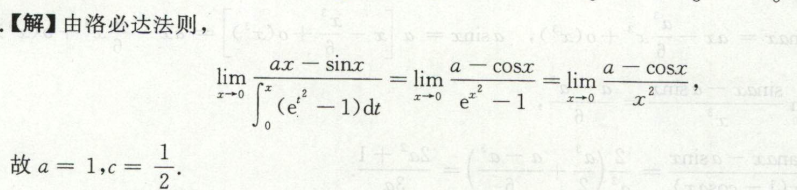
例10
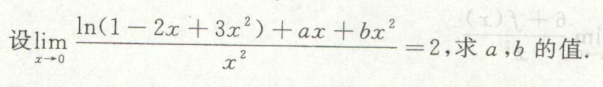

例11
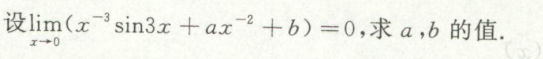
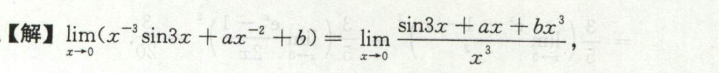

例12

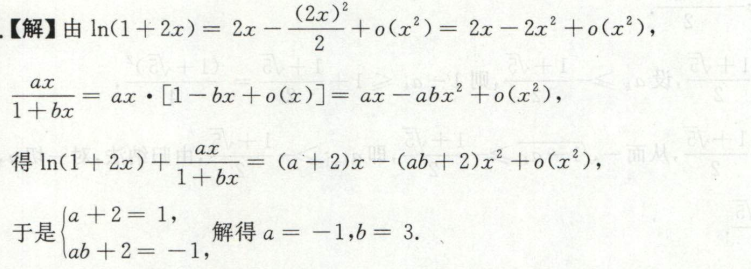
例13
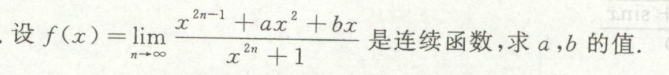

此题需要根据x的不同讨论极限值,然后根据连续性来做
已知极限求新极限
主要方法有:
1)想办法从待求极限中凑出已知极限,消去
2)根据已知极限得分子分母无穷小阶数高低关系,可以得到一些值
例1
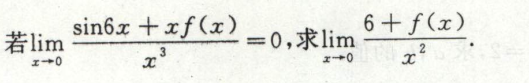

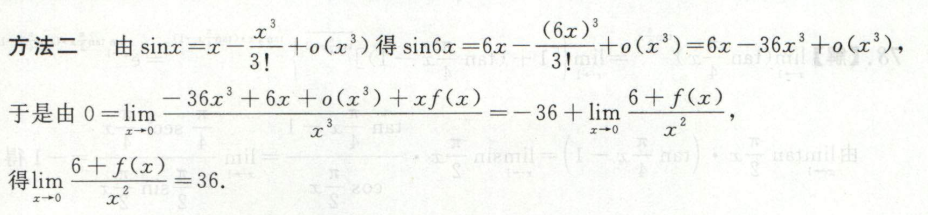
例2
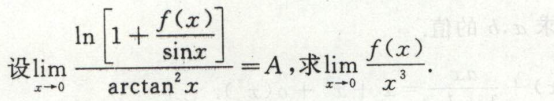
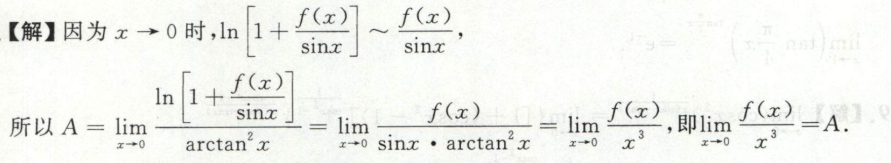
例3


例4
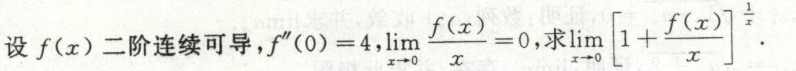

比较无穷小阶数高低
泰勒展开后比较是比较方便的
例1

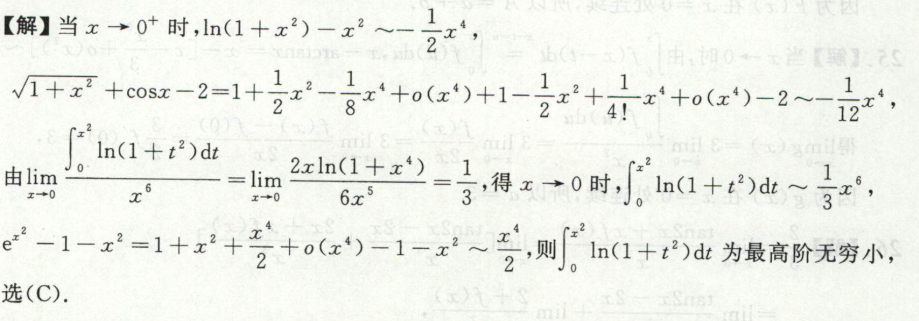
例2

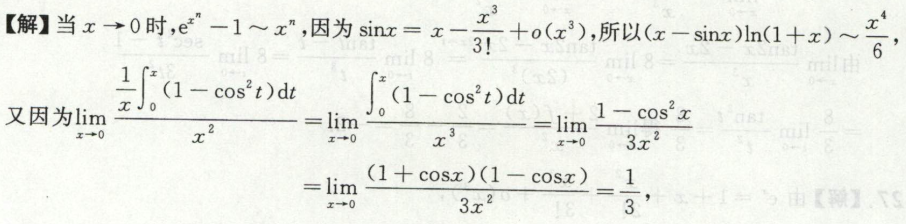
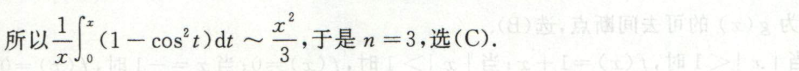
例3

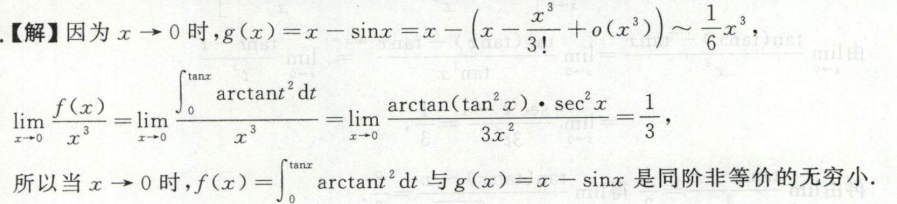
比值求极限判断
例1


例2

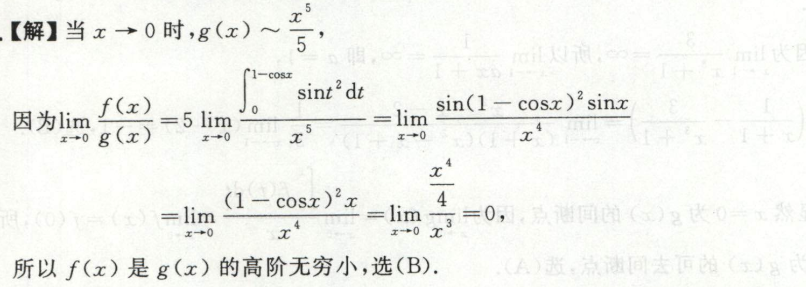
证明极限存在与否
数列极限存在的证明
数列单调有界,则数列收敛,极限存在
极限为A代入递推式可得A
例1
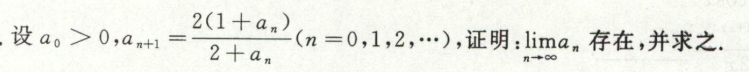

例2



例3
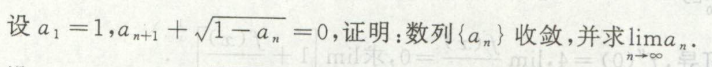

单调有界必收敛,设极限为A代入递推式可得A
反证极限不存在
例1
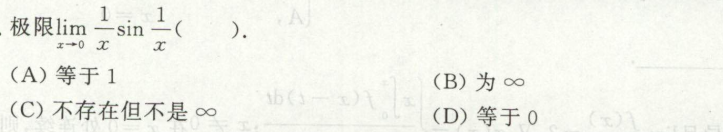
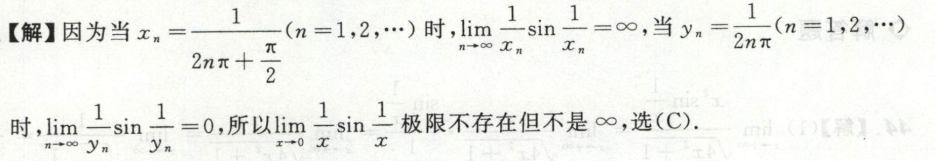
例2

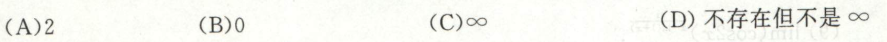
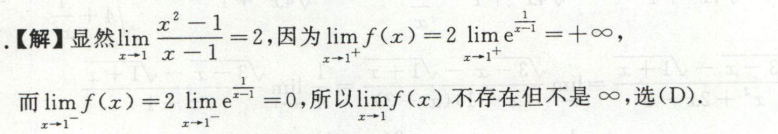
例3


极限函数的分段讨论
极限函数连续性的讨论
例1
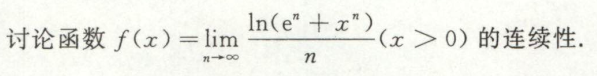

间断点类型的判断
例1



例2
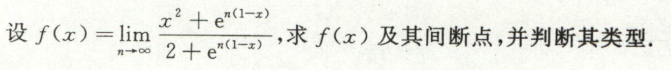
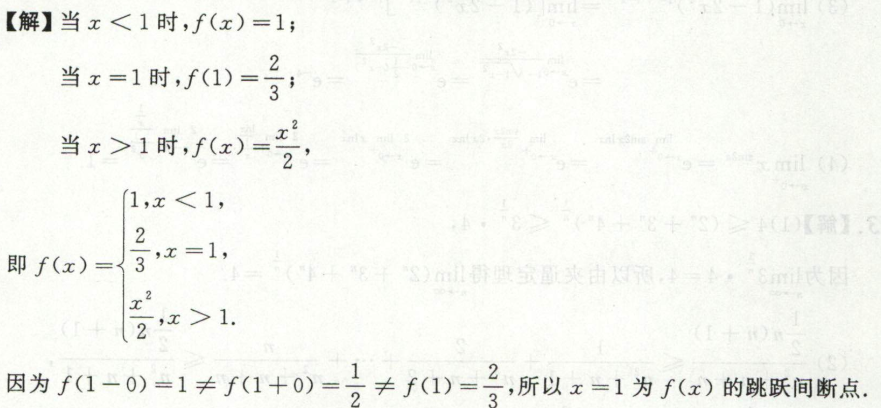
例3

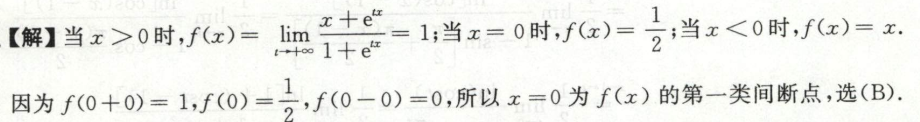
例4
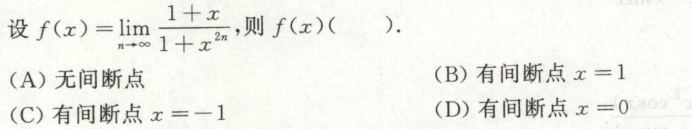

例5
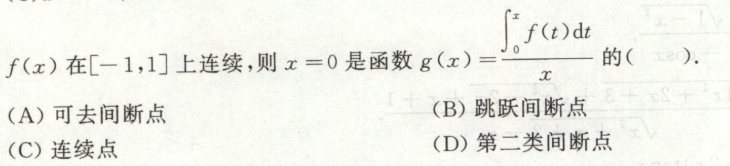
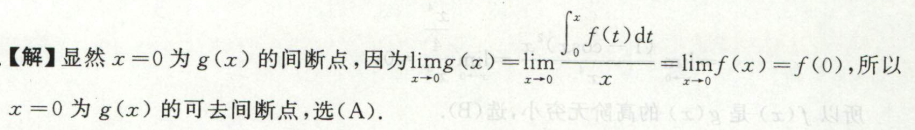
例6


例7
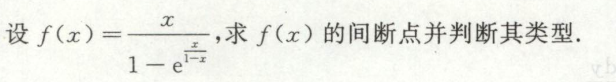
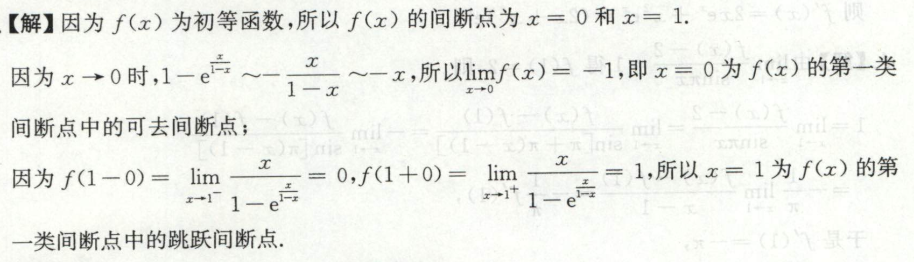
例8
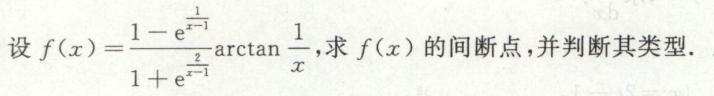

例9