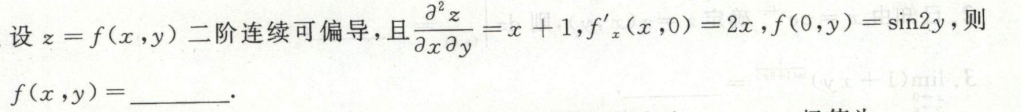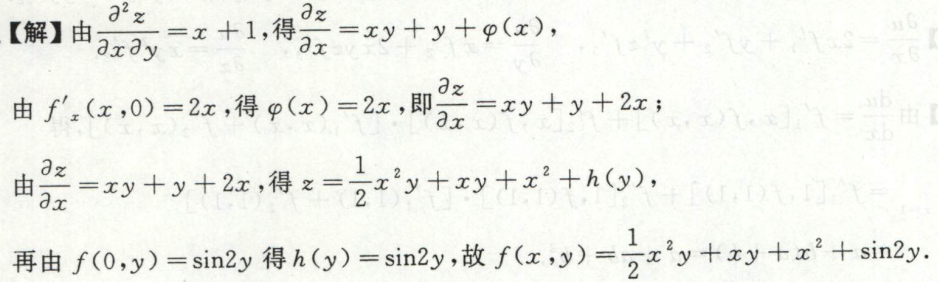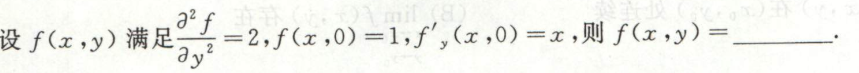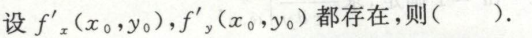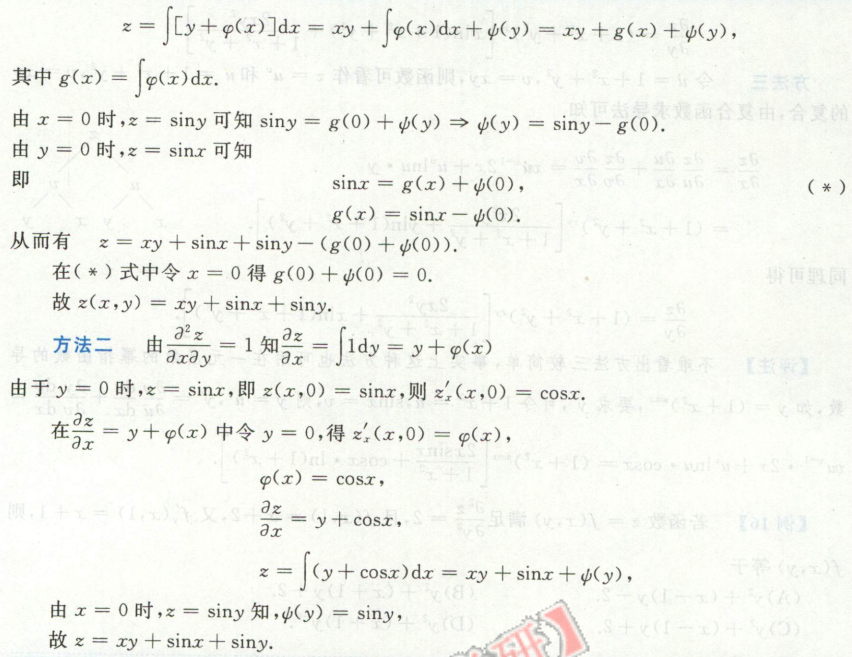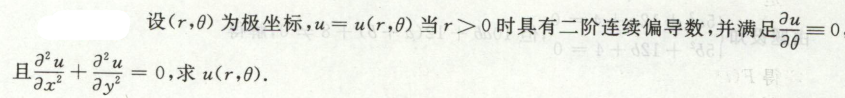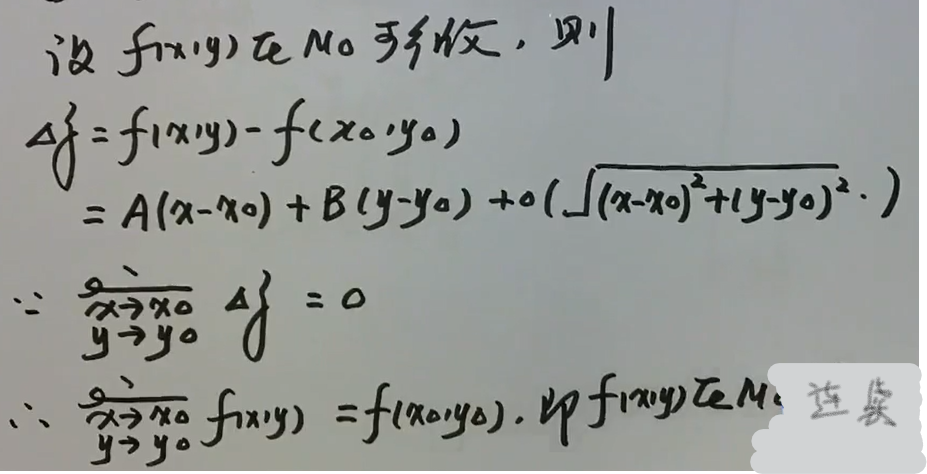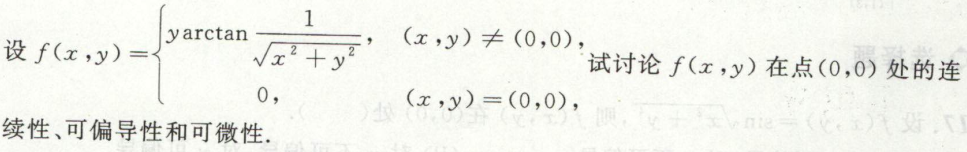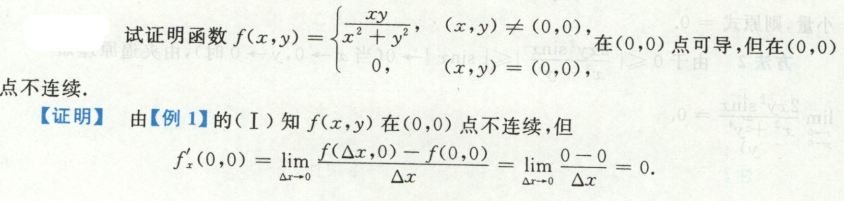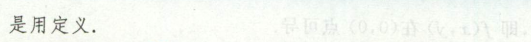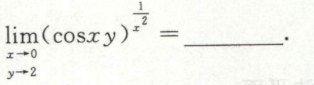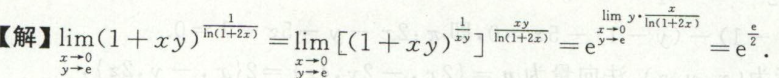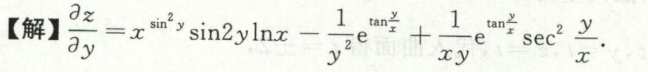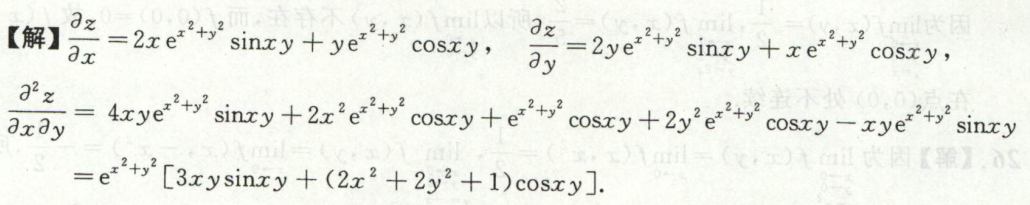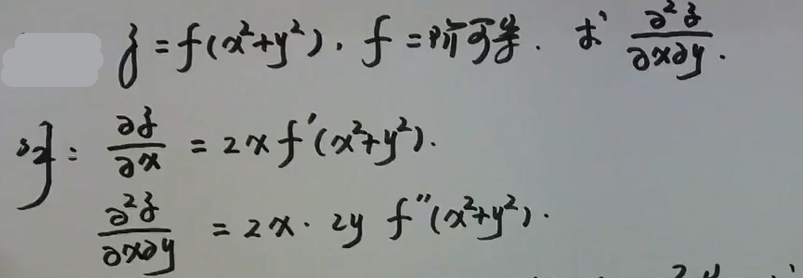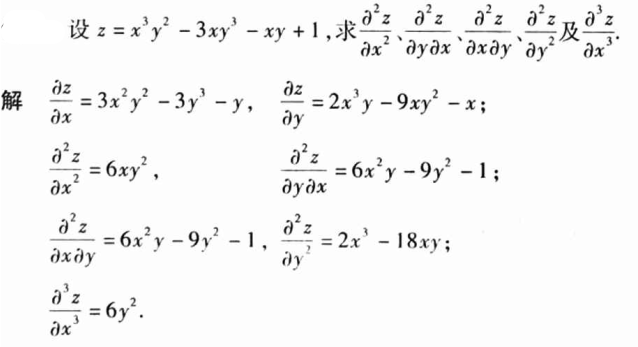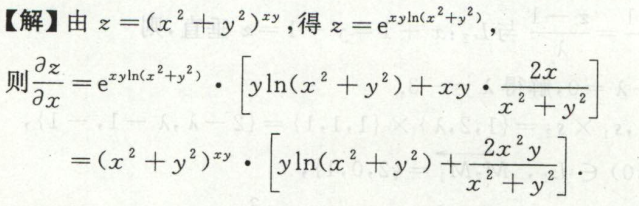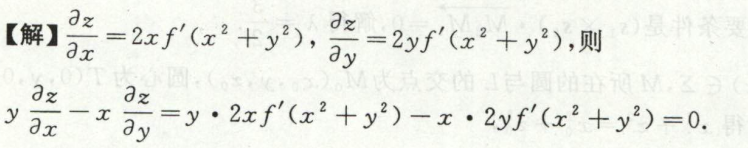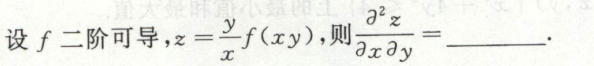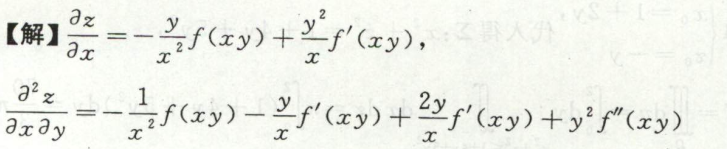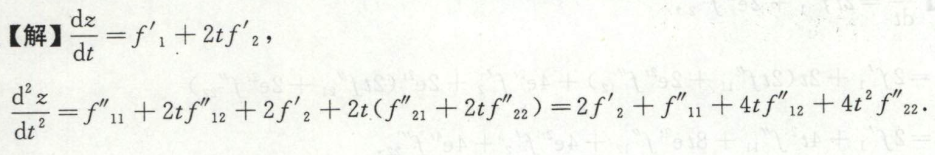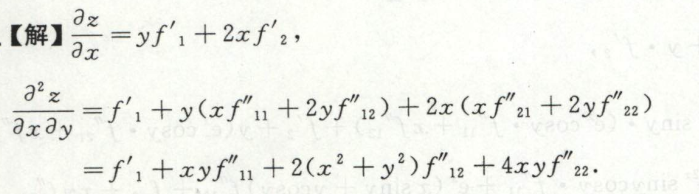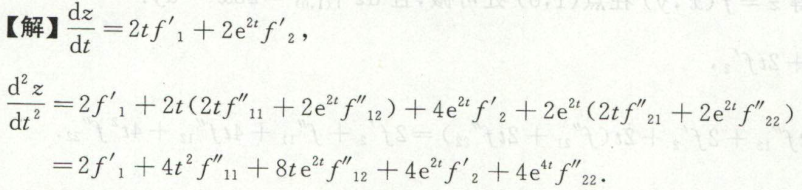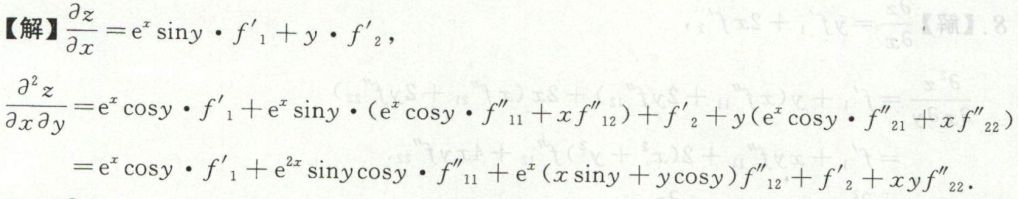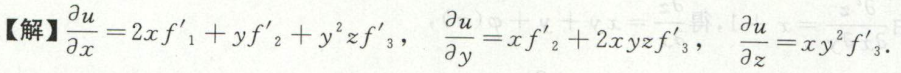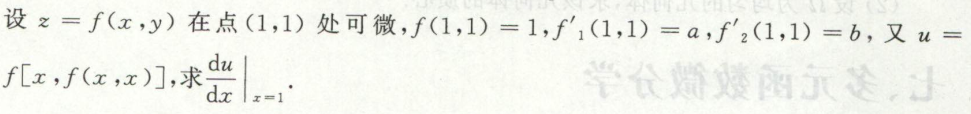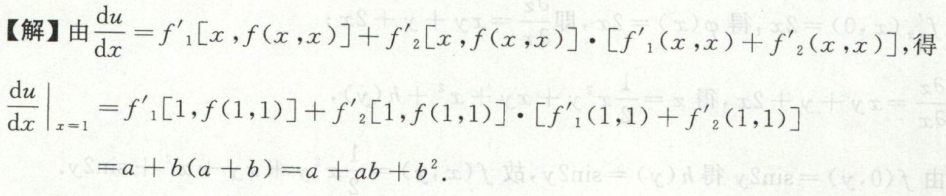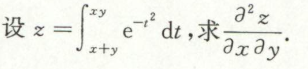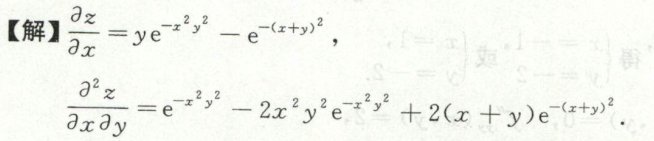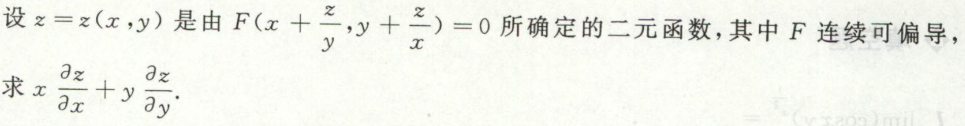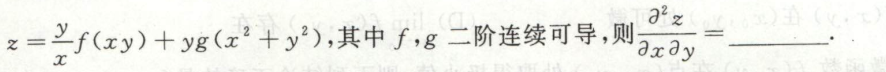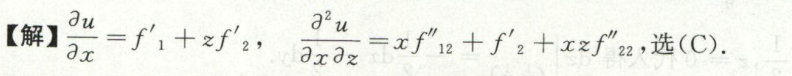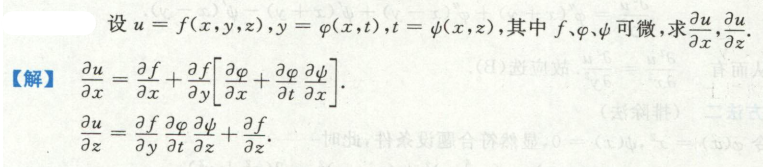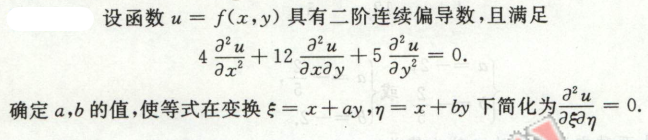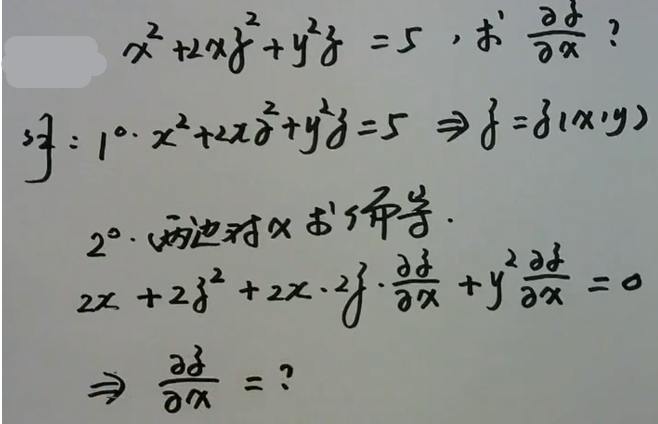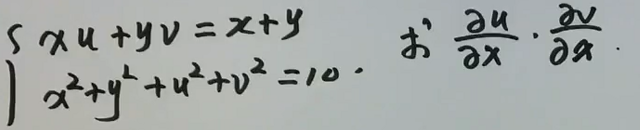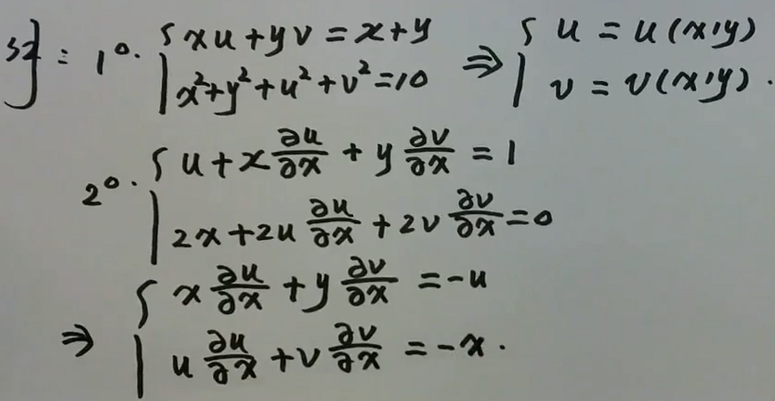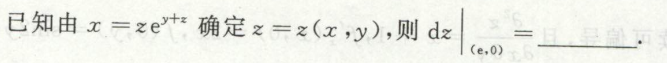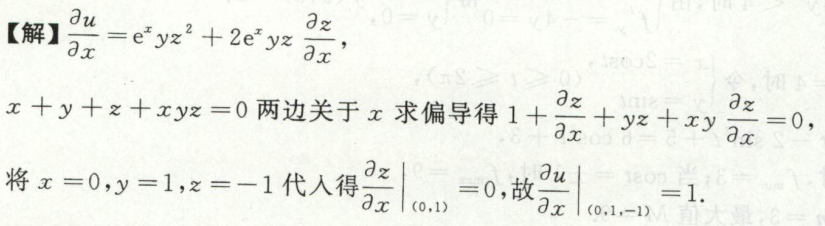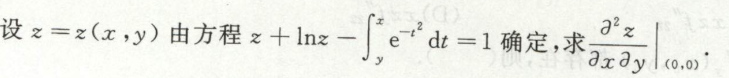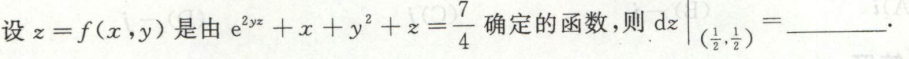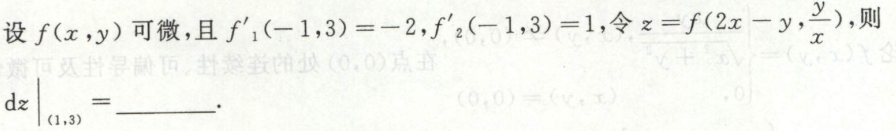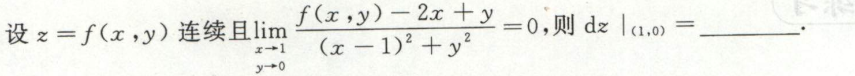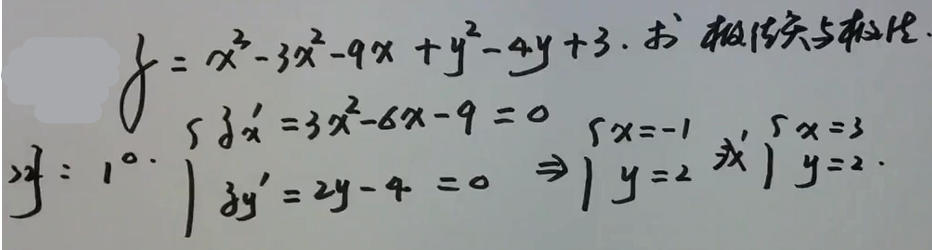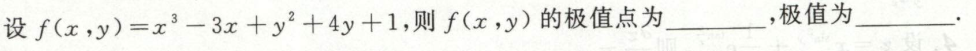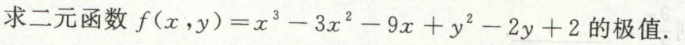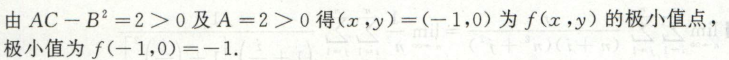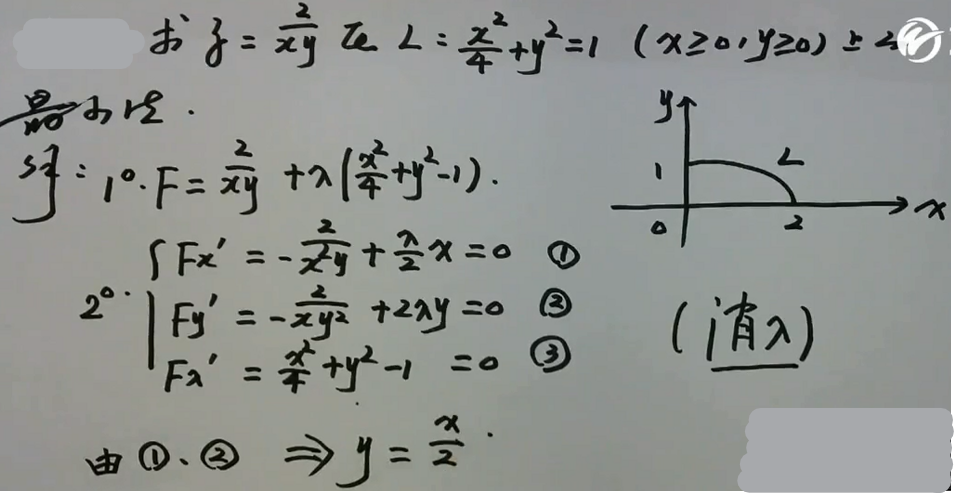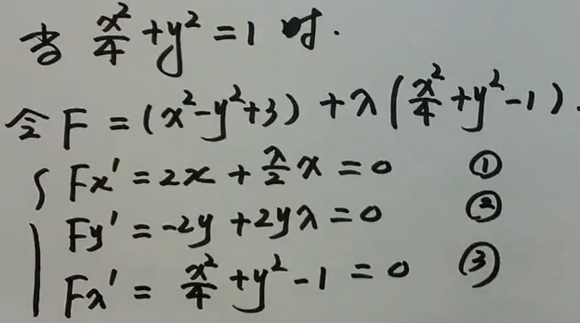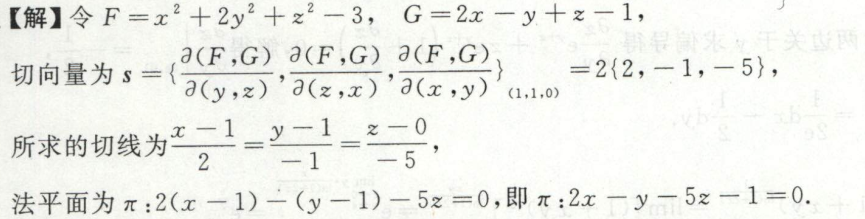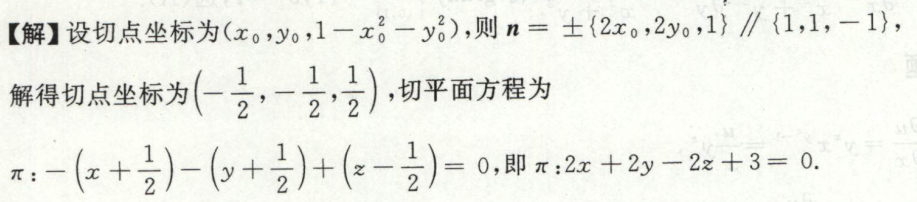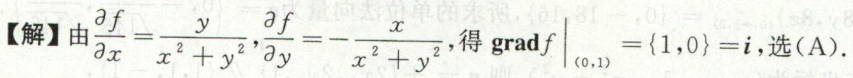高等数学-多元微分学习题
考察多元函数定义、极限存在、连续性、可微、可偏导、泰勒定理
多元函数的定义
例1
image-20200702122423759例2
image-20200702122611230偏导数的定义
偏导数是把多元函数其中一元看作变量，其他元看作常数后，求函数的变化率（求导）
例1
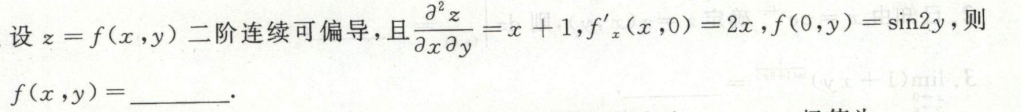image-20200709144415604
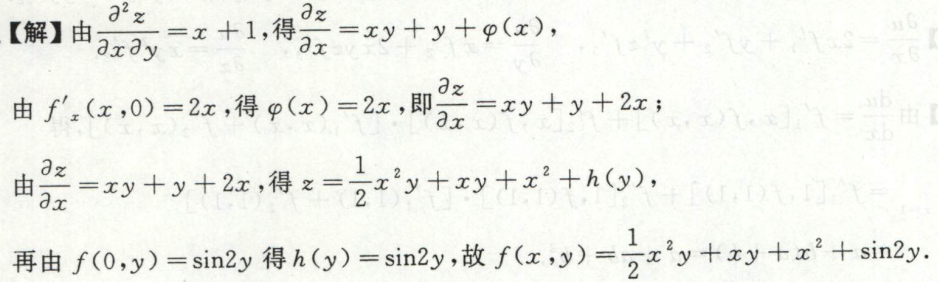image-20200709144432350例2
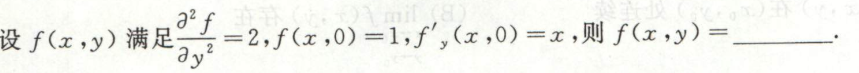image-20200710163615194
image-20200710163631402例3
image-20200710231400530
image-20200710231418304
image-20200710231429789例4
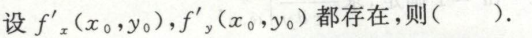image-20200711000314135
image-20200711000327726
image-20200711000344744例5
image-20200713145337218例6
image-20200713145652539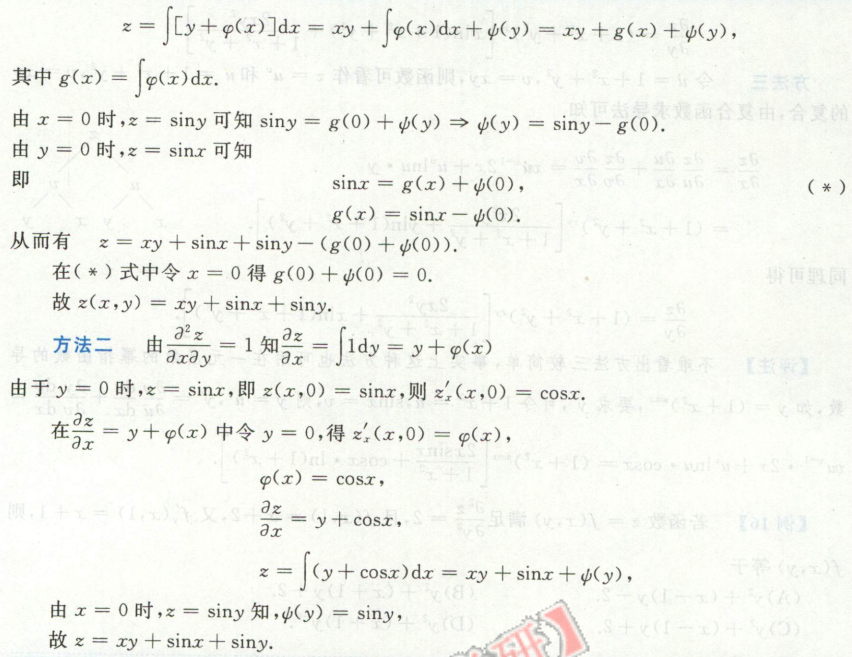
image-20200713145725465例7
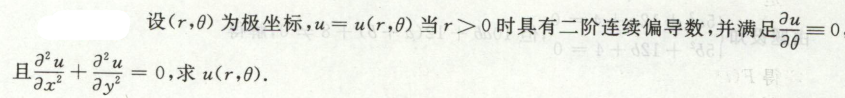image-20200713162205205
image-20200713162250977极值的定义
例1
image-20200710232139022
image-20200710232158542例2
image-20200713175333243例3
image-20200713180142424
image-20200713180435932例4
image-20200714171451504连续不一定可偏导，可偏导不一定连续
例1 连续不一定可偏导，可偏导不一定连续
image-20200711093916297
image-20200711093943298可微必连续
例1 证明可微必连续
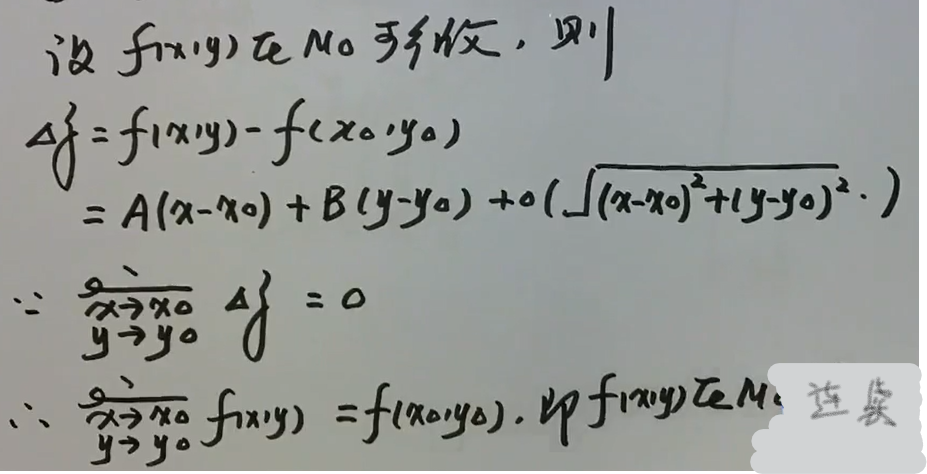
可微必可导
例1 证明可微必可偏导
求证：如果函数 \(z=f(x, y)\) 在点 \((x, y)\) 可微分,那么该函数在点\((x, y)\) 的偏导数 \(\frac{\partial z}{\partial x}\) 与 \(\frac{\partial z}{\partial y}\) 必定存在 \(,\) 且函数 \(z=f(x, y)\) 在点 \((x, y)\) 的全微分为\(\mathrm{d} z=\frac{\partial z}{\partial x} \Delta x+\frac{\partial z}{\partial y} \Delta y\)
image-20200701153847161例2 可微必可偏导
image-20200711002100508
image-20200711002115138连续可偏导必可微
例1 证明连续可偏导必可微
image-20200701160132385
image-20200701160157106例2
image-20200713122053068连续性、可偏导、可微的判断
连续性判断： 用连续定义判断：求该点处的极限，若极限值=对应点值，则连续。否则存在某路径极限值\(\neq\)对应点值，在该点不连续。
可偏导性的判断： 用偏导数的定义判断/求偏导数
可微的判断： 1）可微的定义判断 2）函数连续可偏导必可微 3）可微必可偏导、可微必连续的逆否命题：不可偏导一定不可微、不连续一定不可微
例1 函数连续性、可偏导性、可微的判断
image-20200711094459424
image-20200711094523571例2 函数连续性、可偏导性、可微性的判断
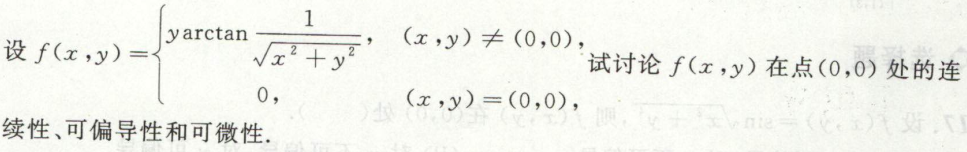image-20200711094918489
image-20200711094933694
image-20200711094948922例3 函数连续性的判断
image-20200712233234132例4 函数连续性、可偏导性的判断
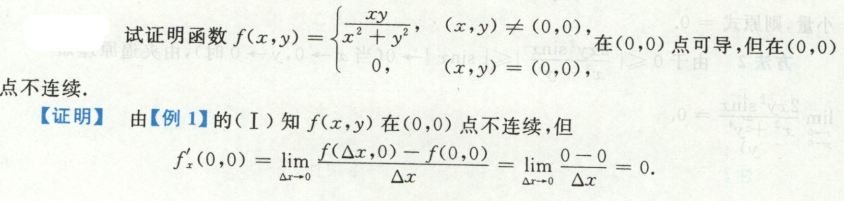image-20200712234029517
image-20200712234115590例5 函数连续性、可偏导性、可微性的判断
image-20200713121706344
image-20200713112654421例6 可微的判断
2020-7-13-001例7 可微的判断
2020-7-13-002例8 可微的判断
image-20200713143156817
image-20200713143240883二元函数泰勒定理
例1
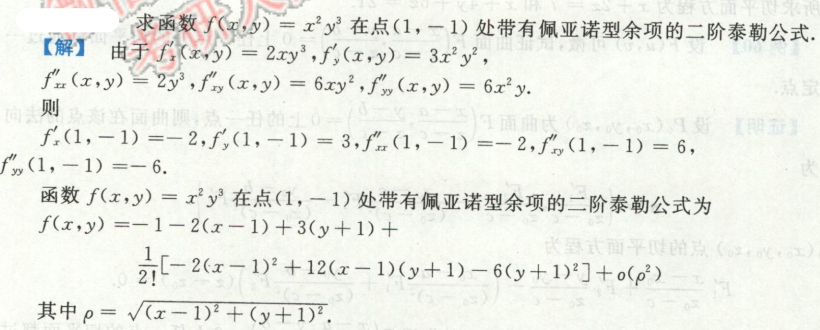image-20200714173833094极限的证明与计算
例1
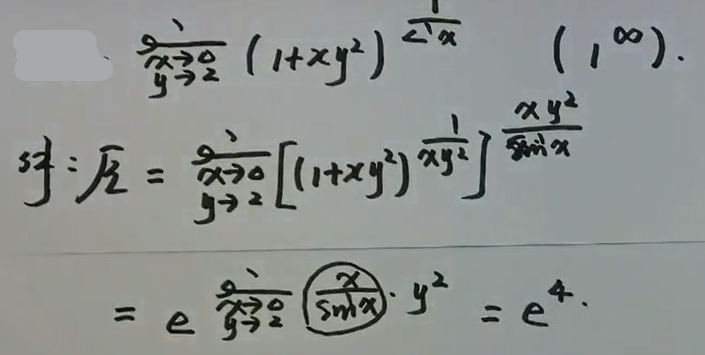image-20200627234136112例2
image-20200627234814941例3
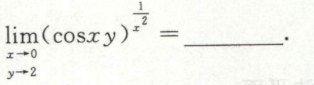image-20200709115331124
image-20200709115355220例4
image-20200710153926439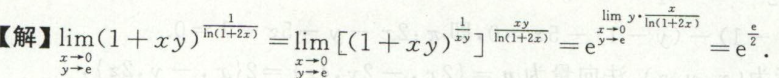
image-20200710154008168例5
2020-7-12-001偏导数的计算
普通多元函数偏导数的计算
例1
image-20200630193622716例2
image-20200630193722483例3
image-20200630194820210例4
image-20200710154605029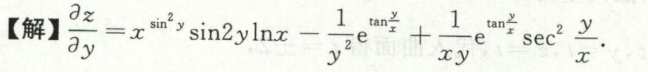
image-20200710154631336例5
image-20200710163046837
image-20200710163102165例6
image-20200710170255824
image-20200710170316137例7
image-20200711100253125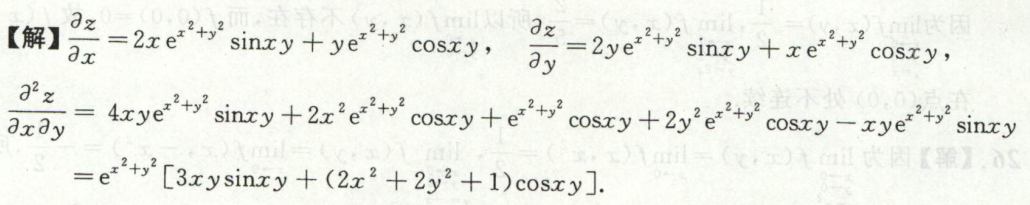
image-20200711100317734例8
image-20200712233907028例9
image-20200713144242620例10
image-20200713144708235多元复合函数偏导数的计算
例1
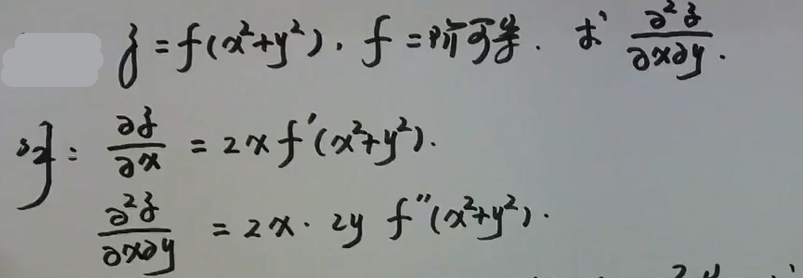image-20200701200713256例2
image-20200701201025937例3
image-20200701201356400例4
image-20200630195731232
image-20200630195748789例5
image-20200630200109237例6
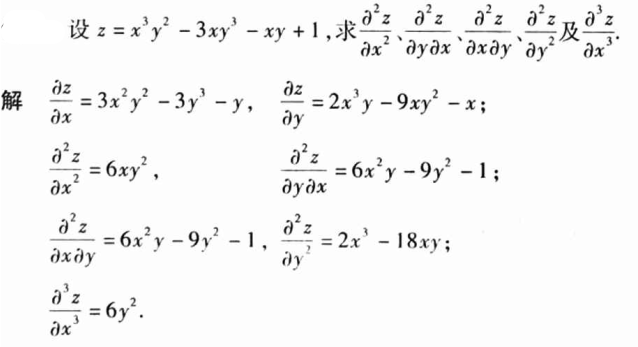image-20200630210624138例7
image-20200630210717628例8
image-20200630211047597
image-20200630211557621例9
image-20200709115723584
image-20200709115812472例10
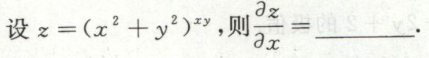image-20200709115841168
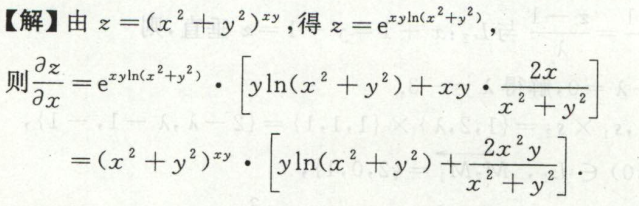image-20200709115857916例11
image-20200709115925231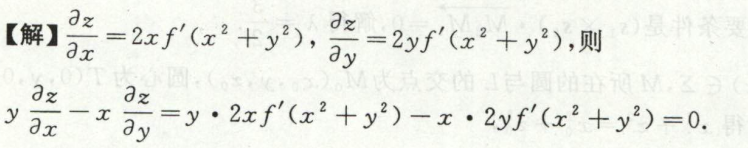
image-20200709120026906例12
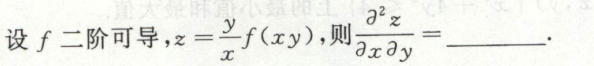image-20200709120054695
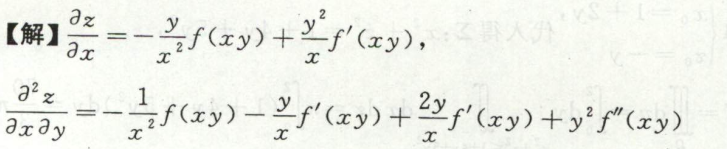image-20200709120109524
image-20200709120119794例13
image-20200709142509529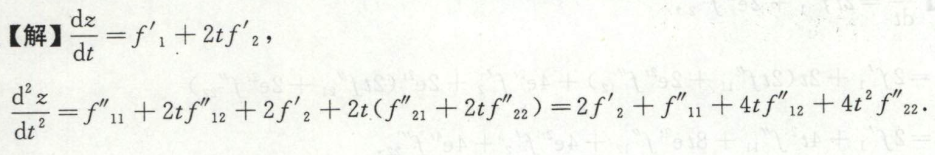
image-20200709142521539例14
image-20200709143454804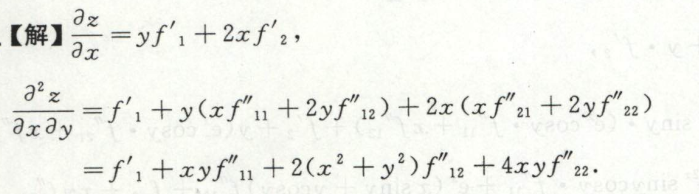
image-20200709143509307例15
image-20200709154525460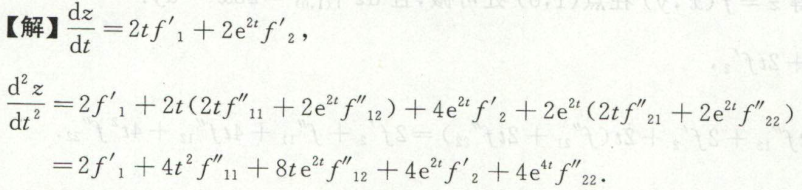
image-20200709154545305例16
image-20200709155415509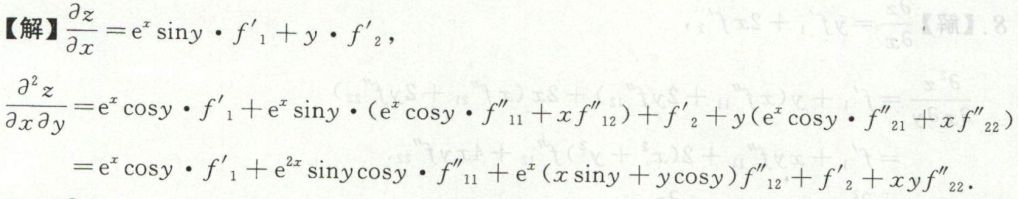
image-20200709155447245例17
image-20200709160119364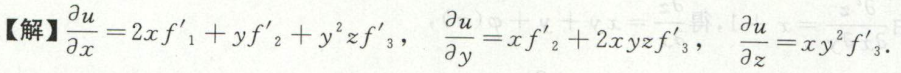
image-20200709160139480例18
注意一下这里偏导数代入的是不同的值
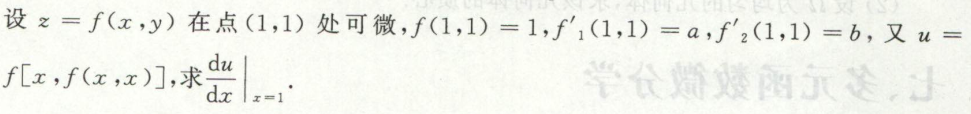image-20200709173236549
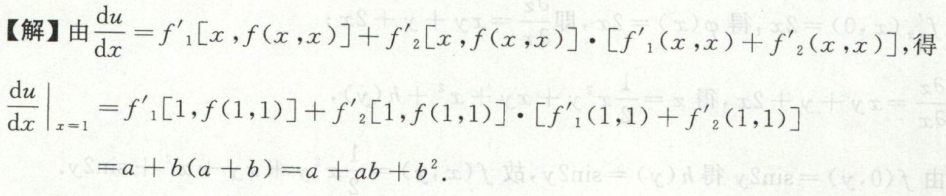image-20200709173254867例19
与变限积分函数复合，求偏导
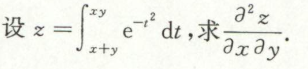image-20200709174135042
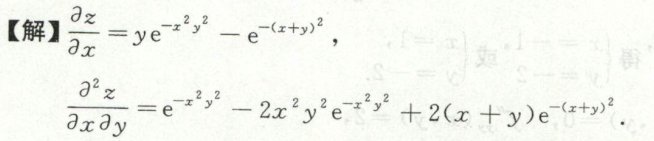image-20200709174240062例20
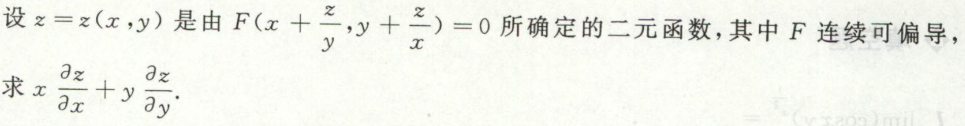image-20200709234842860
image-20200709234859286
image-20200709234911899例21
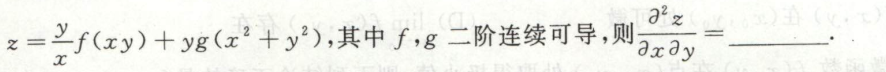image-20200710164338334
image-20200710164317757例22
image-20200711000042513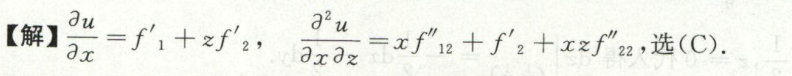
image-20200711000059017例23
image-20200711021616926
image-20200711021632092例24
image-20200711095417822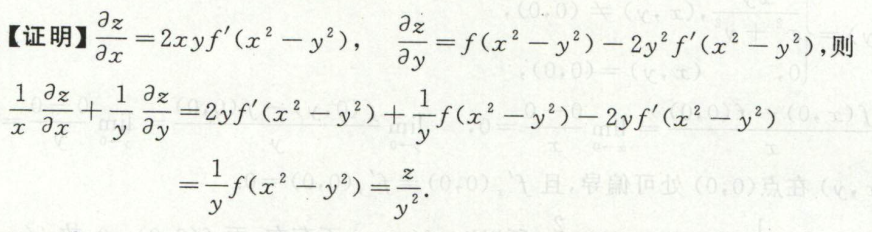
image-20200711095435151例25
image-20200711100817437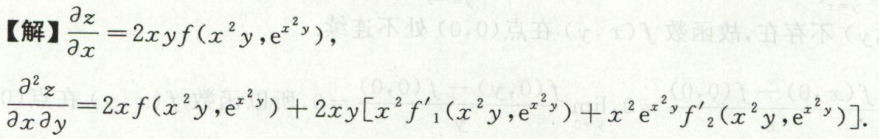
image-20200711100836952例26
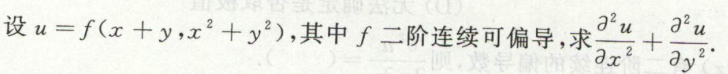image-20200711101447402
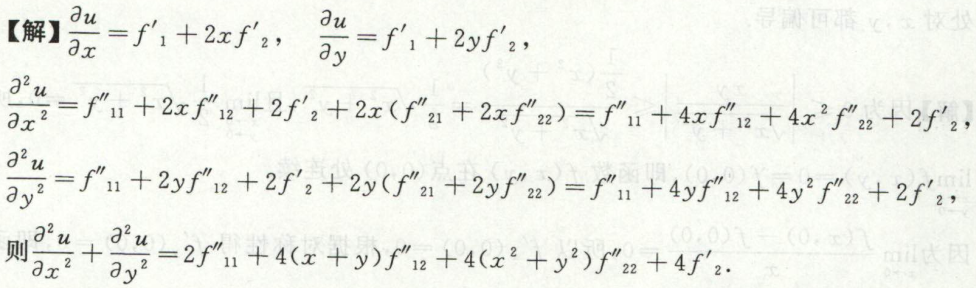image-20200711101524524例27
image-20200711142518827
image-20200711142540183例28
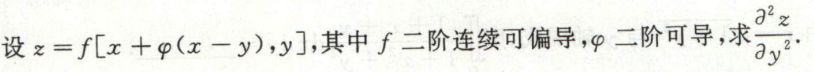image-20200711145058043
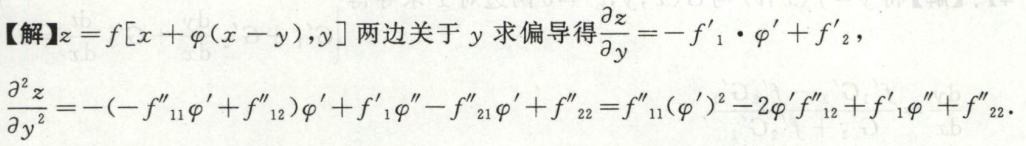image-20200711145114756例29 换元/换坐标系
image-20200711174231552
image-20200711174416018例30 换元/换坐标系
拉普拉斯算子在直角坐标系与柱坐标系中的转换
参考：拉普拉斯算子的百度百科
高数同济第七版P82的证明：
还有csdn上博主的证明（与高数同济7的证明类似）：https://blog.csdn.net/u013102281/article/details/70800631
例31
image-20200713145045588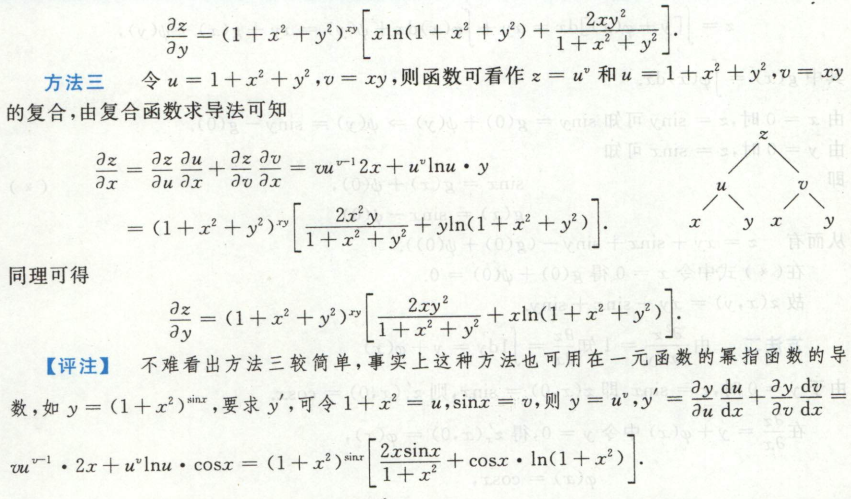
image-20200713145111578例32 换元求偏导
image-20200713151645364例33
image-20200713151858650
image-20200713151924146例34
image-20200713154407255例35
image-20200713154521245例36
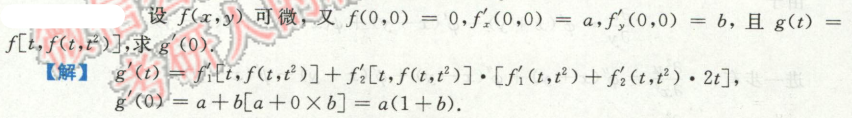image-20200713154634020例37
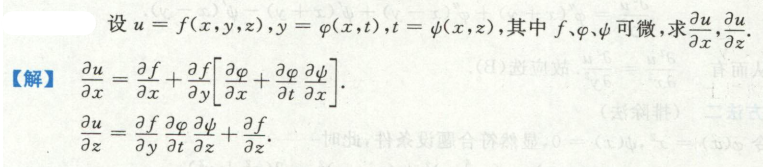image-20200713154828736例38
image-20200713155004931
image-20200713155029885例39
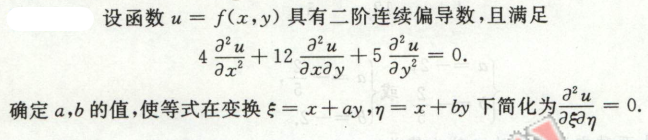image-20200713155411573
image-20200713155430337
image-20200713155500516例40
image-20200713155710640例41
image-20200713164313638
image-20200713164329698多元隐函数及方程组的偏导数的计算
例1
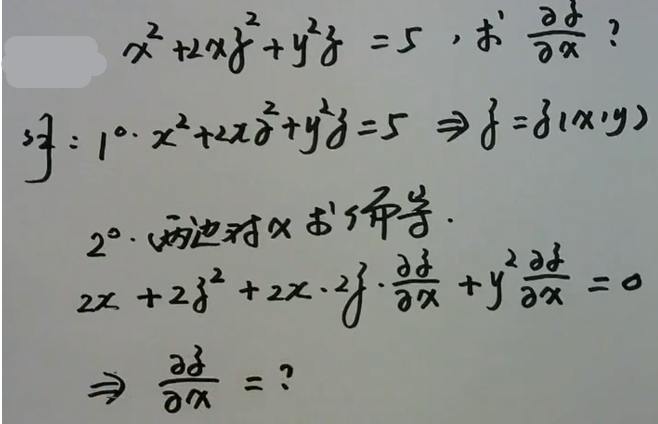image-20200701212558284例2
image-20200701212659511
image-20200701212735480例3
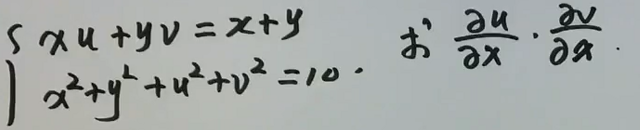image-20200701212826072
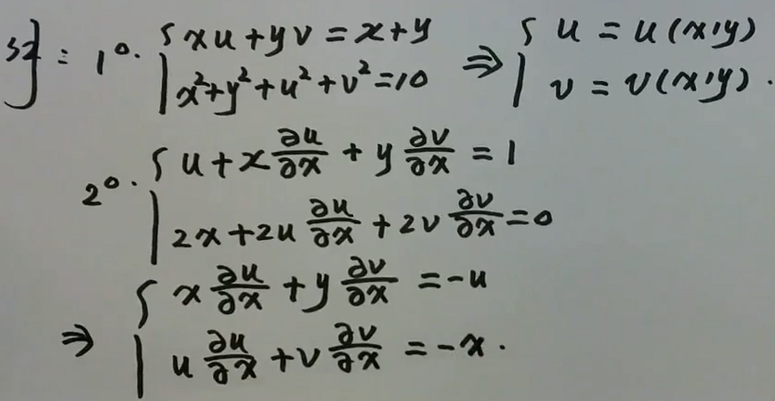image-20200701212911399例4
image-20200709174823501
image-20200709174847696例5
image-20200710152612800
image-20200710152657856
image-20200710152709808例6
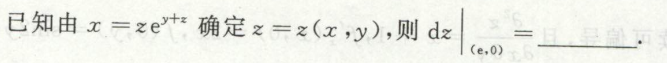image-20200710153357691
image-20200710153415151例7
image-20200710165737474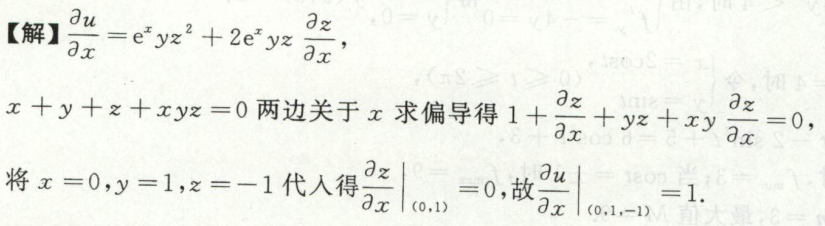
image-20200710165753162例8
image-20200710224305058
image-20200710224325962例9
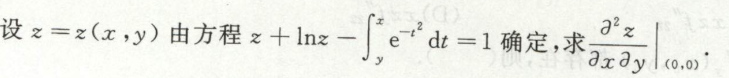image-20200711144441151
image-20200711144456888
image-20200711144509027例10
image-20200711153505138
image-20200711153526825例11
image-20200711161144323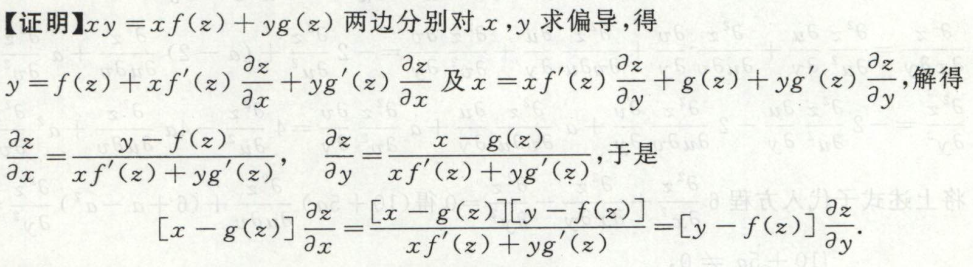
image-20200711161210227例12
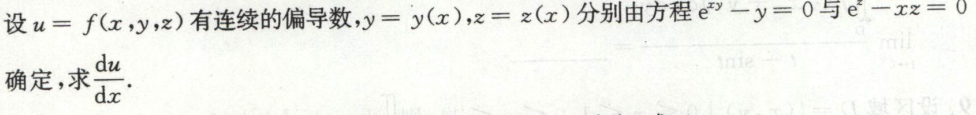image-20200711163849897
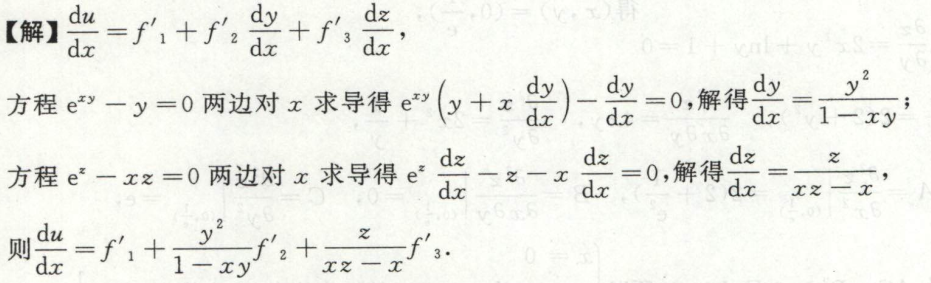image-20200711163919111例13
image-20200711165501946
image-20200711165515724例14
image-20200713164500200例15
image-20200713164614010例16
image-20200713170815177例17
image-20200713171146400
image-20200713171208604例18
image-20200713172355080
image-20200713172420207例19
image-20200713172633692
image-20200713172657470例20
image-20200713172803624全微分的计算
已知函数或隐函数求全微分
求多元函数的全微分，可以对函数两边取微分，直接得全微分。 如果是多元隐函数，或者方程组，可以对方程两边求各自由元的偏导数。利用偏导数得全微分。
例1
image-20200701160321599例2
image-20200701160424316例3
image-20200701160500466例4
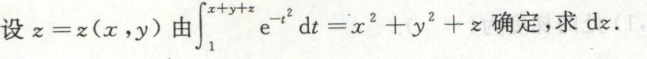image-20200710171131701
image-20200710171144572
image-20200710171201393例5
image-20200710174148525
image-20200710174205081例6
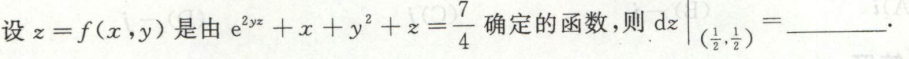image-20200710190655625
image-20200710190627751例7
image-20200711161935902
image-20200711161957276例8
image-20200713144527388例9
image-20200713164912265
image-20200713164941986
image-20200713165017710例10
image-20200713165329798
image-20200713165356281
image-20200713165427769已知部分偏导信息求全微分
例1
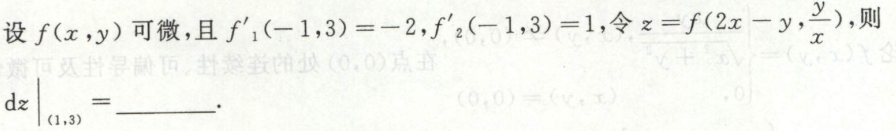image-20200710231039990
image-20200710231054533已知极限求全微分
例1
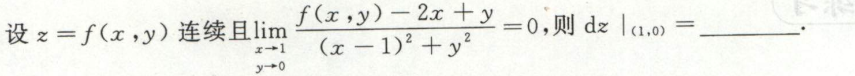image-20200709141641366
image-20200709141659190已知全微分求参数
例1
image-20200713151304137多元微分学代数应用：求多元函数极值
极值/最值问题，其实就是最优化问题。
注意：极值问题，可能取值的的位置，包括驻点、不可导点、边界点。
无条件极值的定义域为开区域，考虑的是定义域内的驻点是否取极值。 条件极值多了约束，考虑的是有约束的情况下是否取极值。（如果约束正好是对应无条件极值的边界，则条件极值考虑的是边界点是否取极值）
例如求 \(f(x, y)\) 在区域 \(D=\left\{(x, y) \mid x^{2}+4 y^{2} \leqslant 4\right\}\) 上的极值/最值。 可以拆成两部分来求： 在区域 \(D_1=\left\{(x, y) \mid x^{2}+4 y^{2} < 4\right\}\) 上找到所有的驻点判断是否取极值（求非条件极值） 在区域 \(D_2=\left\{(x, y) \mid x^{2}+4 y^{2} = 4\right\}\) 上，即给定约束\(x^{2}+4 y^{2} = 4\)的条件下，求函数的极值（求条件极值）
实际问题中，很多问题只在开区域内取最值，这个时候，可以不考虑在边界上取极值的情况（不用考虑条件极值）
无条件极值
无条件极值要求定义域为开区域
例1
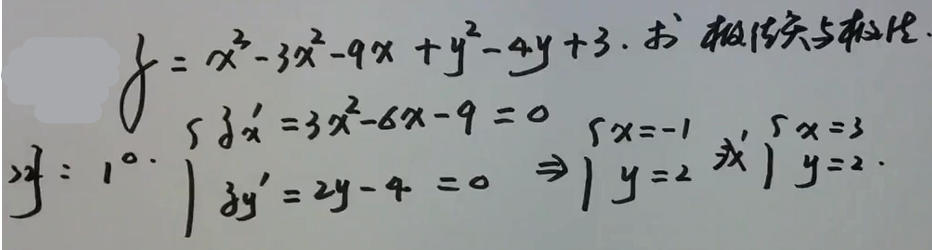image-20200702141609968
image-20200702141658206
image-20200702141724267例2
image-20200702161848747例3
image-20200702175100751
image-20200702175142248例4
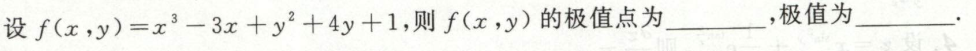image-20200709145620862
image-20200709145647649例5
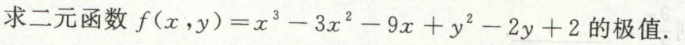image-20200710004826182
image-20200710004844257例6
image-20200711175523494
image-20200711175542673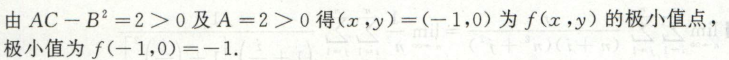
image-20200711175556778例7
image-20200713174057577例8
image-20200713174313120
image-20200713174444313例9
image-20200713174830286
image-20200713174845204
image-20200713174923357条件极值
例1
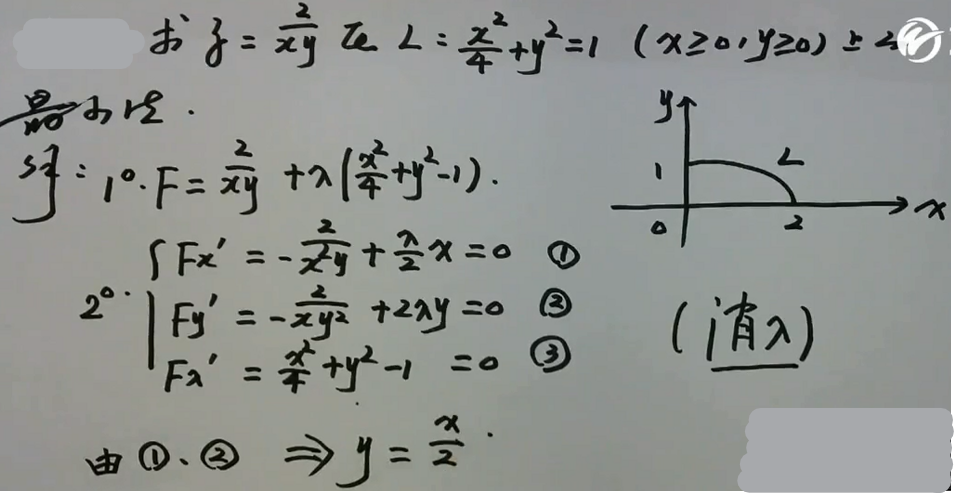image-20200702142508895
image-20200702142300367例2
image-20200702145537603
image-20200702145744521
image-20200702153214607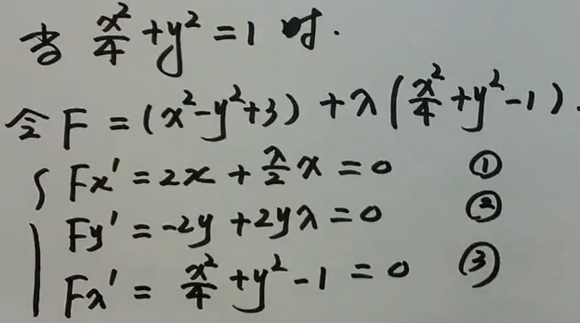
image-20200702153235382
image-20200702153315765
image-20200702153506463例3
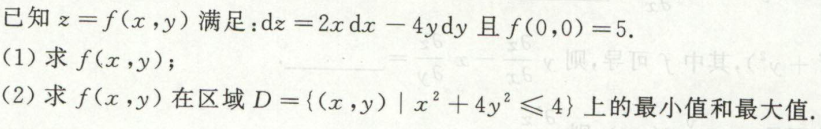image-20200710014254265
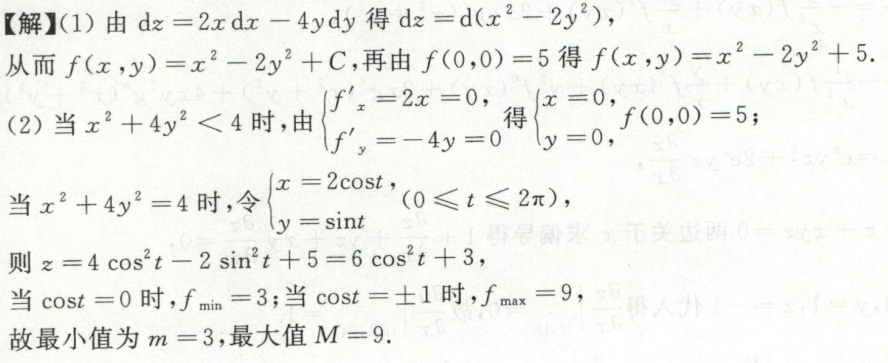image-20200710014312491例4
image-20200711181129008
image-20200711181146986例5
image-20200711181341127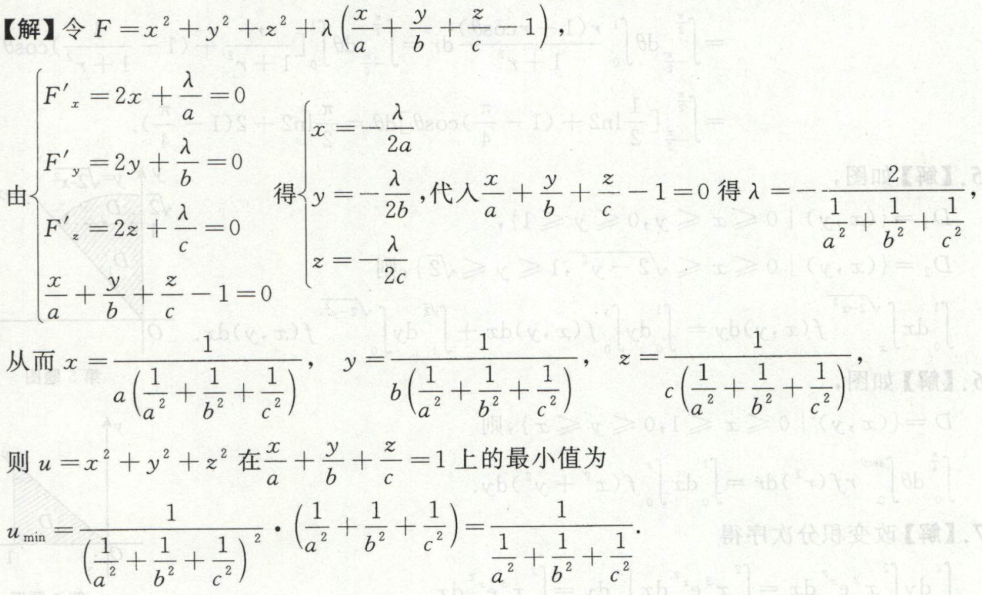
image-20200711181403270例6
image-20200714094854267例7
image-20200714095236251例8
image-20200714095257751例9
image-20200714095619978例10
image-20200714095639483例11
image-20200714100156436
image-20200714100220455
image-20200714100235332例12
image-20200714101350571
image-20200714101413487例13
image-20200714102547365
image-20200714102604930例14
image-20200714104559159
image-20200714104623138
image-20200714104643751例15
image-20200714110123747
image-20200714110146199多元微分学几何/向量分析应用：
空间曲线切向量和曲面法向量
空间曲线切向量的计算
切向量为\((x_t^\prime, y_t^\prime, z_t^\prime)\)或者\((1,\frac{dy}{dx}, \frac{dz}{dx})\)
参考答案是代隐函数方程组求偏导的Jacobi公式。实际上，求解过程一般就是解\(\frac{dy}{dx}, \frac{dz}{dx}\)的线性方程组的过程。
例1
image-20200710000637459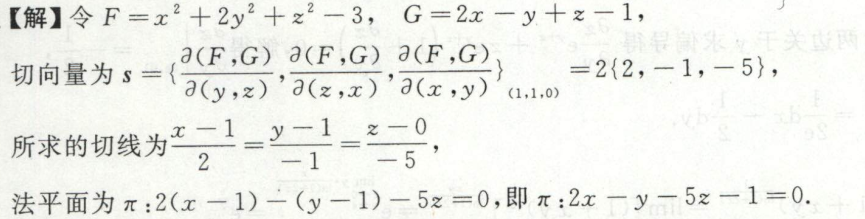
image-20200710000906166空间曲面法向量的计算
空间曲面\(F(x,y,z)\)上任一点法向量为\((F_x,F_y,F_z)\)
例1
image-20200710003635901
image-20200710003714077例2
image-20200710225148524
image-20200710225203730例3
image-20200710225711507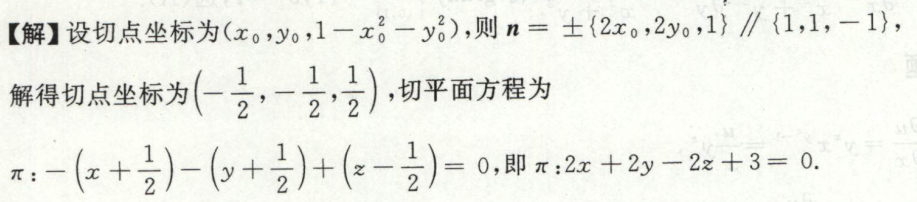
image-20200710225733691例4
image-20200714171630294例5
image-20200714172346614
image-20200714172406509
image-20200714172426559例6
image-20200714172716526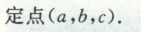
image-20200714172733799例7
image-20200714173030959例8
image-20200714173216173向导数与梯度的计算
方向导数的计算
（方向导数是个值哦，不是向量；只是因为和梯度联系紧密，放到了这里）
例1
image-20200709150645947
image-20200709150733278
image-20200709150806992例2
image-20200714145005840例3
image-20200714145208186
image-20200714145231469例4
image-20200714145523955梯度的计算
例1
image-20200709151252431
image-20200709151310235例2
image-20200711002502273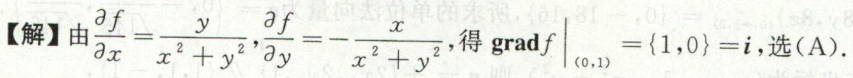
image-20200711002516936例3
image-20200714150327874
image-20200714150354285
image-20200714150415782例4
image-20200714170902723
image-20200714170922899