高等数学-多元微积分-多元微分学-向量值函数和向量分析

一元向量值函数 \(f: D \rightarrow \mathbf{R}^{n}\)

一元向量值函数定义

定义 设数集 \(D\subset R\),则称映射 \(f: D \rightarrow \mathbf{R}^{n}\) 为一元向量值函数, 通常记为\(\boldsymbol{r}=\boldsymbol{f}(t), t \in D\) 其中数集 D 称为函数的定义域, , t称为自变量, \(\boldsymbol{r}\) 称为因变量.

例子：空间解析几何的参数方程形式，就是向量值函数

空间曲线\(\Gamma\)的参数方程就是一个一元向量值函数， \(\left\{\begin{array}{l}x=\varphi(t) \\ y=\psi(t), \quad t \in[\alpha, \beta] \\ z=\omega(t)\end{array}\right.\) 也可以写成向量形式： \(\boldsymbol{r}=x \boldsymbol{i}+y \boldsymbol{j}+z \boldsymbol{k}, \quad \boldsymbol{f}(t)=\varphi(t) \boldsymbol{i}+\psi(t) \boldsymbol{j}+\omega(t) \boldsymbol{k}\) 简记为向量方程： \(\boldsymbol{r}=\boldsymbol{f}(t), t \in[\alpha, \boldsymbol{\beta}]\)

一元向量值函数的极限

定义 2 设向量值函数 \(f(t)\) 在点 \(t_{0}\) 的某一去心邻域内有定义,如果存在一 个常向量 \(\boldsymbol{r}_{0},\) 对于任意给定的正数 \(\varepsilon,\) 总存在正数 \(\delta,\) 使得当 \(t\) 满足 \(0<\left|t-t_{0}\right|<\delta\)时，对应的函数值 \(\boldsymbol{f}(t)\) 都满足不等式\(\left|\boldsymbol{f}(t)-\boldsymbol{r}_{0}\right|<\varepsilon\), 那么,常向量 \(\boldsymbol{r}_{0},\) 就叫做向量值函数 \(\boldsymbol {f(t)}\) 当 \(t \rightarrow t_{0}\) 时的极限 \(,\) 记作\(\lim _{t \rightarrow t_{0}} \boldsymbol f(t)=\boldsymbol r_{0} \quad\) 或 \(\quad \boldsymbol{f}(t) \rightarrow \boldsymbol{r}_{0}, l \rightarrow t_{0}\)

向量值函数 \(\boldsymbol {f(t)}\) 当 \(t \rightarrow t_{0}\) 时极限存在的充分必要条件是：三个分量函数 \(f_{1}(t), f_{2}(t), f_{3}(t)\) 当 \(t \rightarrow t_{0}\) 时的极限都存在。 即\(\lim _{t \rightarrow t_{0}} \boldsymbol f(t)=\left(\lim _{t \rightarrow t_{0}} f_{1}(t), \lim _{t \rightarrow t_{0}} f_{2}(t), \lim _{t \rightarrow t_{0}} f_{3}(t)\right)\)

一元向量值函数的连续性

向量值函数 \(\boldsymbol {f(t)}\) 在\(t_{0}\) 连续的充分必要条件是：三个分量函数 \(f_{1}(t), f_{2}(t), f_{3}(t)\) 都在在\(t_{0}\) 连续

一元向量值函数的导数或导向量

向量值函数 \(\boldsymbol {f(t)}\) 在\(t_{0}\)的某邻域内有定义， 如果\(\lim _{\Delta t \rightarrow 0} \frac{\boldsymbol\Delta r}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{\boldsymbol f\left(t_{0}+\Delta t\right)-\boldsymbol f\left(t_{0}\right)}{\Delta t}\)， 则称这个极限向量是此一元向量值函数的导数或导向量，记为\(\boldsymbol{f}^{\prime}\left(t_{0}\right)\) 或 \(\left.\frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} t}\right|_{t=t_{0}}\)

向量值函数 \(\boldsymbol {f(t)}\) 在\(t_{0}\) 可导的充分必要条件是：三个分量函数 \(f_{1}(t), f_{2}(t), f_{3}(t)\) 都在在\(t_{0}\) 可导。 即\(\boldsymbol{f}^{\prime}\left(t_{0}\right)=f_{1}^{\prime}\left(t_{0}\right) \boldsymbol{i}+f_{2}^{\prime}\left(t_{0}\right) \boldsymbol{j}+f_{3}^{\prime}\left(t_{0}\right) \boldsymbol{k}\)

一元向量值函数的导数运算法则，与数量函数的导数运算法则形式相同： \(\frac{\mathrm{d}}{\mathrm{d} t} \boldsymbol{C}=\mathbf{0}\) \(\frac{\mathrm{d}}{\mathrm{d} t}[c \boldsymbol{u}(t)]=c \boldsymbol{u}^{\prime}(t)\) \(\frac{\mathrm{d}}{\mathrm{d} t}[\boldsymbol{u}(t) \pm \boldsymbol{v}(t)]=\boldsymbol{u}^{\prime}(t) \pm \boldsymbol{v}^{\prime}(t)\) \(\frac{\mathrm{d}}{\mathrm{d} t}[\varphi(t) \boldsymbol{u}(t)]=\varphi^{\prime}(t) \boldsymbol{u}(t)+\varphi(t) \boldsymbol{u}^{\prime}(t)\) \(\frac{\mathrm{d}}{\mathrm{d} t}[\boldsymbol{u}(t) \cdot \boldsymbol{v}(t)]=\boldsymbol{u}^{\prime}(t) \cdot \boldsymbol{v}(t)+\boldsymbol{u}(t) \cdot \boldsymbol{v}^{\prime}(t)\) \(\frac{\mathrm{d}}{\mathrm{d} t}[\boldsymbol{u}(t) \times \boldsymbol{v}(t)]=\boldsymbol{u}^{\prime}(t) \times \boldsymbol{v}(t)+\boldsymbol{u}(t) \times \boldsymbol{v}^{\prime}(t)\) \(\frac{\mathrm{d}}{\mathrm{d} t} \boldsymbol{u}[\varphi(t)]=\varphi^{\prime}(t) \boldsymbol{u}^{\prime}[\varphi(t)]\)

几何应用：在空间解析几何中的应用：空间曲线切向量、曲面法向量

向量值函数的几何意义

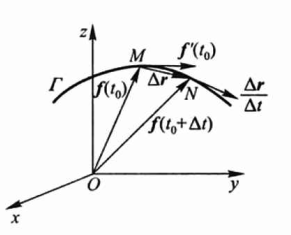
导向量 \(f^{\prime}\left(t_{0}\right)=\lim _{\Delta t \rightarrow 0} \frac{\Delta r}{\Delta t}\) 是向量值函数 \(r=f(t)\) 的终端曲线 \(\Gamma\) 在点 \(M\) 处的一个切向量,其指向与 \(t\) 的增长方向一致.

空间曲线的切线与法平面

空间曲线\(\Gamma\)的参数方程就是一个一元向量值函数， \(\left\{\begin{array}{l}x=\varphi(t) \\ y=\psi(t), \quad t \in[\alpha, \beta] \\ z=\omega(t)\end{array}\right.\) 也可以写成向量形式： \(\boldsymbol{r}=x \boldsymbol{i}+y \boldsymbol{j}+z \boldsymbol{k}, \quad \boldsymbol{f}(t)=\varphi(t) \boldsymbol{i}+\psi(t) \boldsymbol{j}+\omega(t) \boldsymbol{k}\) 简记为向量方程： \(\boldsymbol{r}=\boldsymbol{f}(t), t \in[\alpha, \boldsymbol{\beta}]\)

由前面几何意义可知，导向量是向量值函数变化方向上的切向量。 则向量\(\boldsymbol T=\boldsymbol f^{\prime}\left(t_{0}\right)=\left(\varphi^{\prime}\left(t_{0}\right), \psi^{\prime}\left(t_{0}\right), \omega^{\prime}\left(t_{0}\right)\right)\)就是曲线的一个切向量（要求三个导数不同时为0）（对参数求导组成得导向量） 曲线\(\Gamma\)在点M处的切线方程\(\frac{x-x_{0}}{\varphi^{\prime}\left(t_{0}\right)}=\frac{y-y_{0}}{\psi^{\prime}\left(t_{0}\right)}=\frac{z-z_{0}}{\omega^{\prime}\left(t_{0}\right)}\) 曲线\(\Gamma\)在点M处的法平面方程\(\varphi^{\prime}\left(t_{0}\right)\left(x-x_{0}\right)+\psi^{\prime}\left(t_{0}\right)\left(y-y_{0}\right)+\omega^{\prime}\left(t_{0}\right)\left(z-z_{0}\right)=0\)

对于非参数方程形式的空间曲线，如（显函数形式）： \(\left\{\begin{array}{l}y=\varphi(x) \\ z=\psi(x)\end{array}\right.\) 可以化为参数方程形式求解： \(\left\{\begin{array}{l}x=x \\ y=\varphi(x) \\ z=\psi(x)\end{array}\right.\)

对于另一种非参数方程形式的空间曲线，如（隐函数方程组形式）： \(\left\{\begin{array}{l}F(x, y, z)=0 \\ G(x, y, z)=0\end{array}\right.\) 可以（对方程组求自由元的导数+解线性方程组）的方式来求解,得曲线的切向量\((1,\frac{dy}{dx}, \frac{dz}{dx}) \rightarrow ...\) 看过下一节：曲面的切平面与法线后，可以将\(F(x,y,z)=0\)和\(G(x,y,z)=0\)看作两个曲面，分别求曲面的法向量\(\boldsymbol n_1, \boldsymbol n_2\)，空间曲线是两曲面的交线，空间曲线的切向量\(\boldsymbol n = \boldsymbol n_1 \times \boldsymbol n_2\)

曲面的切平面与法线

曲面方程\(F(x, y, z)=0\) 在曲面\(F(x, y, z)=0\)上，且过曲面上一点\(M(x_0,y_0,z_0)\)的任意曲线，设曲线的参数方程为： \(\left\{\begin{array}{l}x=\varphi(t) \\ y=\psi(t), \quad t \in[\alpha, \beta] \\ z=\omega(t)\end{array}\right.\) 由上一节知，这条空间曲线的切线方程为\(\frac{x-x_{0}}{\varphi^{\prime}\left(t_{0}\right)}=\frac{y-y_{0}}{\psi^{\prime}\left(t_{0}\right)}=\frac{z-z_{0}}{\omega^{\prime}\left(t_{0}\right)}\) \(F[\varphi(t), \psi(t), \omega(t)] \equiv 0\) F有连续偏导数的情况下，\(\left.\frac{\mathrm{d}}{\mathrm{d} t} F[\varphi(t), \psi(t), \omega(t)]\right|_{t=t_{0}}=0\) 即\(F_{x}\left(x_{0}, y_{0}, z_{0}\right) \varphi^{\prime}\left(t_{0}\right)+F_{y}\left(x_{0}, y_{0}, z_{0}\right) \psi^{\prime}\left(t_{0}\right)+F_{z}\left(x_{0}, y_{0}, z_{0}\right) \omega^{\prime}\left(t_{0}\right)=0\) 引入向量\(\boldsymbol{n}=\left(\boldsymbol{F}_{x}\left(x_{0}, y_{0}, z_{0}\right), F,\left(x_{0}, y_{0}, z_{0}\right), F_{z}\left(x_{0}, y_{0}, z_{0}\right)\right)\)，又有（见上一节）过曲面点\(M(x_0,y_0,z_0)\)的任任意曲线切向量\(\boldsymbol{T}=\left(\boldsymbol{\varphi}^{\prime}\left(t_{0}\right), \boldsymbol{\psi}^{\prime}\left(t_{0}\right), \boldsymbol{\omega}^{\prime}\left(t_{0}\right)\right)\) 即\(\boldsymbol T \cdot \boldsymbol n = \boldsymbol 0\) 这个与曲面上过点M的任意曲线切线都垂直的向量\(\boldsymbol{n}=\left(\boldsymbol{F}_{x}\left(x_{0}, y_{0}, z_{0}\right), F,\left(x_{0}, y_{0}, z_{0}\right), F_{z}\left(x_{0}, y_{0}, z_{0}\right)\right)\)，就是空间曲面在\(M(x_0,y_0,z_0)\)处的切平面的法向量，（对隐函数左侧求偏导组成的向量） 对应的切平面方程为\(F_{x}\left(x_{0}, y_{0}, z_{0}\right)\left(x-x_{0}\right)+F_{y}\left(x_{0}, y_{0}, z_{0}\right)\left(y-y_{0}\right)+F_{z}\left(x_{0}, y_{0}, z_{0}\right)\left(z-z_{0}\right)=0\) 法线方程为\(\frac{x-x_{0}}{F_{x}\left(x_{0}, y_{0}, z_{0}\right)}=\frac{y-y_{0}}{F_{y}\left(x_{0}, y_{0}, z_{0}\right)}=\frac{z-z_{0}}{F_{z}\left(x_{0}, y_{0}, z_{0}\right)}\)

对于非隐函数形式的空间曲线，如（显函数形式）： \(z=f(x, y)\) 可以化为隐函数形式： \(F(x, y, z)=f(x, y)-z\) 对应的有： \(F_{x}(x, y, z)=f_{x}(x, y), F_{y}(x, y, z)=f_{y}(x, y), F_{z}(x, y, z)=-1\) 则平面切点M处的法向量： \(\boldsymbol{n}=\left(f_{x}\left(x_{0}, y_{0}\right), f_{y}\left(x_{0}, y_{0}\right),-1\right)\) 法向量单位化（化为方向余弦的形式：z轴向上）： 各分量分别为\(\cos \alpha=\frac{-f_{x}}{\sqrt{1+f_{x}^{2}+f_{y}^{2}}}, \cos \beta=\frac{-f_{y}}{\sqrt{1+f_{x}^{2}+f_{,}^{2}}}, \cos \gamma=\frac{1}{\sqrt{1+f_{x}^{2}+f_{\gamma}^{2}}}\)

物理应用:速度与加速度

由前面几何意义可知，导向量是向量值函数变化方向上的切向量，进一步，可以赋予其物理意义。

设向量值函数\(\boldsymbol{r}=\boldsymbol{f}(t)\)是沿空间光滑曲线运动的质点 \(M\) 的位置向量，t代表时间 \(\boldsymbol{v}(t)=\frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} t}\) 是质点 \(M\) 的速度向里,其方向与曲线相切 \(\boldsymbol{a}(t)=\frac{\mathrm{d} v}{\mathrm{d} t}=\frac{\mathrm{d}^{2} \boldsymbol{r}}{\mathrm{d} t^{2}}\) 是质点 \(M\) 的加速度向量.

多元向量值函数

方向导数（不是向量值函数）

方向导数不是多元向量值函数，但是它与梯度的定义有关，所以把它放到这里。

偏导数反应的是函数沿坐标轴方向的变化率。很多物理现象需要求解物理量沿特定方向的变化率，只靠偏导数数是显然不够的。有必要讨论函数沿特定方向的变化率。（给定方向，只求大小，是个标量）

以二元函数为例，给定\(P_0(x_0,y_0)\)和附近的点\(P(x,y)\),当两点距离\(|PP_0|\)足够小时， \(P_0 P\)可以看作是直线段\(l\)， \(l\)上两点间距离\(|PP_0|=t\)， \(l\)的方向向量\(\boldsymbol e_{l}=(\cos \alpha, \cos \beta)\) 参数方程：\(\left\{\begin{array}{l}x=x_{0}+t \cos \alpha \\ y=y_{0}+t \cos \beta\end{array}(t \geqslant 0)\right.\) 对于函数 \(f(x, y)\) 在 \(P_{0}\left(x_{0}, y_{0}\right)\) 处沿方向 \(l\) 的变化率. 即函数增量与距离的比值，取极限，即\(\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)}=\lim _{t \rightarrow 0^{*}} \frac{f\left(x_{0}+t \cos \alpha, y_{0}+t \cos \beta\right)-f\left(x_{0}, y_{0}\right)}{t}\)，这里\(\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)}\)称作函数的方向导数

对于方向取\(\boldsymbol e_l = \boldsymbol i = (1,0)\),方向导数就是对x的偏导数\(\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)} = f_x|_{(x_0,y_0)}\) 对于方向取\(\boldsymbol e_l = \boldsymbol j = (0,1)\),方向导数就是对y的偏导数\(\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)} = f_y|_{(x_0,y_0)}\)

定理 （方向导数存在的必要条件）如果函数 \(f(x, y)\) 在点 \(P_{0}\left(x_{0}, y_{0}\right)\) 可微分,那么函数在该点沿任一方向\(l\) 的方向导数存在,且有\(\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)}=f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta\)，其中其中 \(\cos \alpha\) 和 \(\cos \beta\) 是方向 \(l\) 的方向余弦. 证明：由函数 \(f(x, y)\) 在点 \(P_{0}\left(x_{0}, y_{0}\right)\) 可微分,得： \(\begin{aligned} & f\left(x_{0}+\Delta x, y_{0}+\Delta y\right)-f\left(x_{0}, y_{0}\right) \\=& f_{x}\left(x_{0}, y_{0}\right) \Delta x+f_{y}\left(x_{0}, y_{0}\right) \Delta y+o(\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}) \end{aligned}\) 又\(\Delta x=t \cos \alpha, \Delta y=t \cos \beta, \sqrt{(\Delta x)^{2}+(\Delta y)^{2}}=t\) 得方向导数： \(\begin{aligned} \left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)}&= \lim _{t \rightarrow 0^{+}} \frac{f\left(x_{0}+t \cos \alpha, y_{0}+t \cos \beta\right)-f\left(x_{0}, y_{0}\right)}{t} \\&= \lim _{t \rightarrow 0^{+}} \frac{f_{x}\left(x_{0}, y_{0}\right) \Delta x+f_{y}\left(x_{0}, y_{0}\right) \Delta y+o(\sqrt{(\Delta x)^{2}+(\Delta y)^{2}})-f\left(x_{0}, y_{0}\right)}{t} \\ &= f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta \end{aligned}\)

同理，对于三元函数 \(f(x, y, z)\) 来说, 它在空间一点 \(P_{0}\left(x_{0}, y_{0}, z_{0}\right)\) 沿方向 \(e_{l}=(cos \alpha, \cos \beta, \cos \gamma )\)的方向导数为 \(\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}, z_{0}\right)}=\lim _{t \rightarrow 0^{*}} \frac{f\left(x_{0}+t \cos \alpha, y_{0}+t \cos \beta, z_{0}+t \cos \gamma\right)-f\left(x_{0}, y_{0}, z_{0}\right)}{t}\) 同样可证，三元函数 \(f(x, y, z)\) 在空间一点 \(P_{0}\left(x_{0}, y_{0}, z_{0}\right)\) 可微，则该函数沿方向 \(\boldsymbol e_{i}=(\cos \alpha, \cos \beta, \cos \gamma)\) 的方向导数为\(\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}, z_{0}\right)}=f_{x}\left(x_{0}, y_{0}, z_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}, z_{0}\right) \cos \beta+f_{z}\left(x_{0}, y_{0}, z_{0}\right) \cos \gamma\)

梯度

二元函数梯度的定义

以二元函数为例，函数 \(f(x, y)\) 在点 \(P_{0}\left(x_{0}, y_{0}\right)\) 可微分,那么函数在该点沿任一方向\(l\) 的方向导数存在,且有$.|{(x{0}, y_{0})}=f_{x}(x_{0}, y_{0}) +f_{y}(x_{0}, y_{0}) = (f_{x}(x_{0}, y_{0}) ,f_{,}(x_{0}, y_{0}) ) (, ) $，其中其中 \(\cos \alpha\) 和 \(\cos \beta\) 是方向 \(l\) 的方向余弦，则\(\boldsymbol e_{l}=(\cos \alpha, \cos \beta)\)是单位方向向量

我们可以将\((f_{x}\left(x_{0}, y_{0}\right) ,f_{,}\left(x_{0}, y_{0}\right) )\)向量（向量值函数），定义为梯度： \(\boldsymbol {grad} f\left(x_{0}, y_{0}\right)=\nabla f\left(x_{0}, y_{0}\right)=f_{x}\left(x_{0}, y_{0}\right) \boldsymbol i+f_{,}\left(x_{0}, y_{0}\right) \boldsymbol j = (f_{x}\left(x_{0}, y_{0}\right) ,f_{,}\left(x_{0}, y_{0}\right) )\) 它是定义在多元函数上的向量值函数，\(D \rightarrow \mathbf{R}^{n}\) ，由标量函数\(f(x,y)\)经过\(\nabla\)算子的操作，映射到向量空间。

那么，方向导数可以看作是梯度和单位方向向量的内积： \(\begin{aligned}\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)} &=f_{x}\left(x_{0}, y_{0}\right) \cos \alpha+f_{y}\left(x_{0}, y_{0}\right) \cos \beta \\ &=\boldsymbol{grad} f\left(x_{0}, y_{0}\right) \cdot \boldsymbol e_{i}=\left|\boldsymbol{grad} f\left(x_{0}, y_{0}\right)\right| \cos \theta \end{aligned}\) 其中\(\theta\)是两个向量的夹角。

梯度方向是方向导数取最大值的方向，梯度的模就是方向导数的最大值。

\(\begin{aligned}\left.\frac{\partial f}{\partial l}\right|_{\left(x_{0}, y_{0}\right)} &=\boldsymbol{grad} f\left(x_{0}, y_{0}\right) \cdot \boldsymbol e_{i}=\left|\boldsymbol{grad} f\left(x_{0}, y_{0}\right)\right| \cos \theta \end{aligned}\)

• 当方向导数和梯度的方向相同时，即\(\theta = 0\)时，方向导数最大，函数增加最快。 梯度方向是方向导数取最大值的方向，梯度的模就是方向导数的最大值。
• 同理，当方向导数和梯度的方向相反时，即\(\theta = \pi\)时，方向导数最小，函数减小最快。 梯度的反方向是方向导数取最小值的方向，梯度模的相反数就是方向导数的最小值。
• 同理，当方向导数和梯度的方向正交时，即\(\theta = \pi / 2\)时，方向导数为0，函数变化率为0。

二元函数等值线的法线方向是梯度方向

二元函数 \(z=f(x, y)\) 在几何上表示一个曲面，它和平面\(z=c\)截得的曲线叫做等值线。 二元函数的等值线\(\left\{\begin{array}{l}z=f(x, y) \\ z=c\end{array}\right.\)有3个变量2个约束1个自由元， 用代入消元或隐函数方程组的方法可求\(\frac{dy}{dx}= -\frac{f_x}{f_y}\), 由前面向量值函数\(\boldsymbol r = x \boldsymbol i + y \boldsymbol j + z \boldsymbol k = (x,y,z)\)的导函数的几何意义可知，向量\((\frac{dx}{dx}, \frac{dy}{dx},\frac{dz}{dx}) = (1, \frac{dy}{dx},0)\)代表空间曲线的切向量，此切向量z分量为0，\(z=c\)平面上切向量分量\((\frac{dx}{dx}, \frac{dy}{dx}) = (1, \frac{dy}{dx})\)，则\(z=c\)平面上法向量为$(1,-)= (1, ) $， 单位化法向量: \(\begin{aligned} \boldsymbol n &=\frac{1}{\sqrt{f_{x}^{2}\left(x_{0}, y_{0}\right)+f_{y}^{2}\left(x_{0}, y_{0}\right)}}\left(f_{x}\left(x_{0}, y_{0}\right), f_{y}\left(x_{0}, y_{0}\right)\right) \\ &=\frac{\nabla f\left(x_{0}, y_{0}\right)}{\left|\nabla f\left(x_{0}, y_{0}\right)\right|} \end{aligned}\) 即二元函数等值线在\(z=c\)平面上的法线方向就是梯度方向

三元函数梯度的定义

类似二元函数梯度（是个向量值函数）的定义，可以定义三元函数的梯度。

只要函数\(f(x,y,z)\)在空间区域D有连续偏导数，在空间中任意点\((x_0,y_0,z_0)\)都可定义梯度

\(\begin{aligned} \operatorname{grad} f\left(x_{0}, y_{0}, z_{0}\right) &=\nabla f\left(x_{0}, y_{0}, z_{0}\right) \\ &=f_{x}\left(x_{0}, y_{0}, z_{0}\right) \boldsymbol{i}+f_{,}\left(x_{0}, y_{0}, z_{0}\right) \boldsymbol{j}+f_{i}\left(x_{0}, y_{0}, z_{0}\right) \boldsymbol{k} \end{aligned}\)

其中\(\nabla =\frac{\partial}{\partial x} i+\frac{\partial}{\partial y} j+\frac{\partial}{\partial z} k\) 称为(三维的) 向量微分算子或 Nabla 算子 \(, \nabla f=\frac{\partial f}{\partial x} i+\frac{\partial f}{\partial y} j+\frac{\partial f}{\partial z} k\)

三元函数等值面的法线方向是梯度方向

曲面\(f(x, y, z)=c\)是函数\(f(x,y,z)\)的等值面，写成标准形式是\(F(x,y,z) = f(x,y,z) - c = 0\), 有3变量1约束2自由元，可求得\((F_x,F_y,F_z) = (f_x, f_y, f_z)\) 由前面的几何意义可知，对于空间曲面（等值面）上任意点\(M(x_0,y_0,z_0)\)，向量\(\left(\boldsymbol{F}_{x}\left(x_{0}, y_{0}, z_{0}\right), F,\left(x_{0}, y_{0}, z_{0}\right), F_{z}\left(x_{0}, y_{0}, z_{0}\right)\right)\)，就是空间曲面（等值面）\(F(x, y, z)=0\)在\(M(x_0,y_0,z_0)\)处的切平面的法向量， 单位化法向量： \(\begin{aligned} \boldsymbol n &=\frac{1}{\sqrt{f_{x}^{2}\left(x_{0}, y_{0}, z_{0}\right)+f_{y}^{2}\left(x_{0}, y_{0}, z_{0}\right)+f_{y}^{2}\left(x_{0}, y_{0}, z_{0}\right)}}\left(f_{x}\left(x_{0}, y_{0}, z_{0}\right), f_{y}\left(x_{0}, y_{0}, z_{0}\right)\right) \\ &=\frac{\nabla f\left(x_{0}, y_{0}, z_{0}\right)}{\left|\nabla f\left(x_{0}, y_{0}, z_{0}\right)\right|} \end{aligned}\)

标量场\(f: \mathbf{R}^{m} \rightarrow \mathbf{R}\)

如果对于空间区域G内的任意一点M，都有一个确定的数量\(f(M)\)，那么称在这片区域G中确定了一个数量场（如温度场、密度场等）。 一个数量场可以用一个数量函数\(f(M)\)来确定。

矢量场\(f: \mathbf{R}^{m} \rightarrow \mathbf{R}^{n}\)

如果对于空间区域G内的任意一点M，如果与M对应的是一个向量\(\boldsymbol F(M)\),那么称在这片区域中确定了 一个矢量场/向量场。（如力场、速度场等） 一个向量场可用一个向量值函数\(\boldsymbol F(M)\)来确定。

如果向量场\(\boldsymbol F(M)\)恰好是某个数量函数\(f(M)\)的梯度，即\(\boldsymbol F(M) = \nabla f(M)\)，这样的向量场\(\boldsymbol F(M)\)称为势场，对应数量函数\(f(M)\)称为势函数

例如：