高等数学-多元微分学
高等数学-多元微分学
极限、连续性、偏导数、全微分定义及性质
多元函数是有多个自由变量的函数,在其上可以定义距离的概念。可以考虑函数的极限、连续性、可导可微性。
多元函数的极限
以二元函数为例,\(\lim _{x \rightarrow x_{0} \atop y \rightarrow y_{0}} f(x, y)=A \Leftrightarrow \forall \varepsilon>0, \exists \delta>0,\) 当 \(0<\sqrt{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}}<\delta\) 时,恒有 \(\quad|f(x, y)-A|<\varepsilon\)
极限性质
| 一元函数 | 多元函数 | ||
|---|---|---|---|
| 定理 | 极限\(\lim _{x \rightarrow x_{0}} f(x)=A\) \(\Leftrightarrow\) \(f\left(x_{0}^{-}\right)=f\left(x_{0}^{+}\right)=A\) | 极限\(\lim _{x \rightarrow x_{0} \atop y \rightarrow y_{0}} f(x, y)=A\)存在,\(\Rightarrow\) 从各路径趋于\((x_0,y_0)\)的函数值\(f(x,y)\)都等于A; 逆否命题也成立:若存在两条路径取得的极限值不同,则极限不存在 | 不相同 |
| 极限运算法则 | 有理运算、复合运算 | 有理运算、复合运算 | 相同 |
| 性质 | 保号性、夹逼性、局部有界性、极限和无穷小的关系 | 保号性、夹逼性、局部有界性、极限和无穷小的关系 | 相同 |
多元函数证明极限存在,只能通过极限定义证明。多元函数证明极限不存在,可选两条路径证明趋于\((x_0, y_0)\)时函数值\(f(x,y)\)不相等。
多元函数的连续性
简言之,函数值等于极限值,即连续。
| 一元函数 | 多元函数 | |
|---|---|---|
| 连续性的定义 | 函数\(f(x)\)在\(x_0\)的邻域内有定义(在定义域内),且\(\lim _{x \rightarrow x_{0}} f(x)=f\left(x_{0}\right)\),则函数\(f(x)\)在\(x_0\)连续 | 函数\(f(x,y)\)在\((x_0,y_0)\)的邻域内有定义(在定义域内),且\(\lim _{x \rightarrow x_{0} \atop y \rightarrow y_{0}} f(x, y)=A\),则函数\(f(x,y)\)在\(x_0\)连续 |
| 连续函数定理(性质) | 有界性定理、最值定理、介值定理 | 有界性定理、最值定理、介值定理 |
| 连续函数的和差积商与复合(性质) | 连续函数的和差积商均是连续函数,连续函数的复合函数仍为连续函数 | 连续函数的和差积商均是连续函数,连续函数的复合函数仍为连续函数 |
| 初等函数的连续性 | 一元初等函数在其定义域内处处连续 | 多元初等函数在其定义域内处处连续 |
偏导数
一元函数研究函数的变化率时,引入了导数概念。研究多元函数的变化率时,先从一个变量看起。即首先考虑多元函数沿某一自变量的变化率。
偏导数的定义
以多元函数的某一变元做看作变量,而其他变元暂时看作常量,用一元微分学方式求导,得到的就是偏导数。
以二元函数为例,设 \(z=f(x, y)\) 在 \(P_{0}\left(x_{0}, y_{0}\right)\) 的某邻域内有定义,给自变量 \(x\) 以增量 \(\Delta x,\) 而 \(y\) 保持不变(即 \(\left.y=y_{0}\right),\) 相应地得到函数关于 \(x\) 的偏增量\(\Delta_{x} z=f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)\) 如果极限\(\lim _{\Delta x \rightarrow 0} \frac{\Delta_{x} z}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)}{\Delta x}\)存在,则该被极限值就称为 \(z=f(x, y)\) 在 \(P_{0}\left(x_{0}, y_{0}\right)\) 改对变量 \(x\) 的偏导数,记为\(\frac{\partial z}{\partial x} \mid\left(x_{0}, y_{0}\right), \frac{\partial f\left(x_{0}, y_{0}\right)}{\partial x}\) 或 \(f_{x}^{\prime}\left(x_{0}, y_{0}\right)\)
即\(f_{x}^{\prime}\left(x_{0}, y_{0}\right)=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)}{\Delta x}\)
同理\(f^{\prime}_{y}\left(x_{0}, y_{0}\right)=\lim _{\Delta y \rightarrow 0} \frac{f\left(x_{0}, y_{0}+\Delta y\right)-f\left(x_{0}, y_{0}\right)}{\Delta y}\)
对于一元函数来说,\(\frac{dy}{dx}\)可以看作函数微分\(dy\)与自变量微分\(dx\)的商。而偏微分的记号是一个整体记号,不能看作分子分母之商。(如高等数学-多元微分学习题.md#偏微分的计算#例5)
偏导数的几何意义
沿特定轴向的斜率

高阶偏导数
二阶偏导数为例:
\(\frac{\partial}{\partial x}\left(\frac{\partial z}{\partial x}\right)=\frac{\partial^{2} z}{\partial x^{2}}=f_{x x}(x, y), \quad \frac{\partial}{\partial y}\left(\frac{\partial z}{\partial x}\right)=\frac{\partial^{2} z}{\partial x \partial y}=f_{x y}(x, y)\) \(\frac{\partial}{\partial x}\left(\frac{\partial z}{\partial y}\right)=\frac{\partial^{2} z}{\partial y \partial x}=f_{y x}(x, y), \quad \frac{\partial}{\partial y}\left(\frac{\partial z}{\partial y}\right)=\frac{\partial^{2} z}{\partial y^{2}}=f_{y}(x, y)\)
定理 \(\quad\) 如果函数 \(z=f(x, y)\) 的两个二阶混合偏导数 \(\frac{\partial^{2} z}{\partial y \partial x}\) 及 \(\frac{\partial^{2} z}{\partial x \partial y}\) 在区域 \(D\) 内 连续, 那么在该区域内这两个二阶混合偏导数必相等。
偏导数的计算
对于一元函数来说,\(\frac{dy}{dx}\)可以看作函数微分\(dy\)与自变量微分\(dx\)的商。而偏微分的记号是一个整体记号,不能看作分子分母之商。(如高等数学-多元微分学习题.md#偏微分的计算#例5)
普通多元函数偏导数的计算
由于偏导数只有一个变量在动,其他变量看作常量,按一元函数求微分的方式计算即可。
多元复合函数偏导数的计算
概括起来就是:链式求导法则计算
复合函数\(z=f(u,v)\)连续可偏导, \(u=\varphi (t), v = \psi(t)\)
\(\frac{\mathrm{d} z}{\mathrm{d} t}=\frac{\partial z}{\partial u} \frac{\mathrm{d} u}{\mathrm{d} t}+\frac{\partial z}{\partial v} \frac{\mathrm{d} v}{\mathrm{d} t}\)
复合函数\(z=f(u,v)\)连续可偏导,$ u=(x,y), v = (x,y)$
\(\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u} \frac{\partial u}{\partial x}+\frac{\partial z}{\partial v} \frac{\partial v}{\partial x}\) \(\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u} \frac{\partial u}{\partial y}+\frac{\partial z}{\partial v} \frac{\partial v}{\partial y}\)
复合函数\(z=f(u,v)\)连续可偏导,$ u=(x,y), v = (y)$
\(\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u} \frac{\partial u}{\partial x}\) \(\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u} \frac{\partial u}{\partial y}+\frac{\partial z}{\partial v} \frac{\mathrm{d} v}{\mathrm{d} y}\)
在坐标变换中的应用
算子(对函数的操作)在不同坐标系中的转换
拉普拉斯算子在直角坐标系与柱坐标系中的转换
参考:拉普拉斯算子的百度百科
高数同济第七版P82的证明:


还有csdn上博主的证明(与高数同济7的证明类似):https://blog.csdn.net/u013102281/article/details/70800631
隐函数偏导数的计算
对于隐函数方程组,设有m=a+b个变量。 约束条件(函数)个数 = 受约束的变量的个数 =隐含的因变量个数,设为a; 不受约束的变量的个数 = 自变量个数 ,设为b; 则由隐函数方程组,可确定 a个b元函数。 从隐函数方程组中选定b个变量做自变量,剩余的a个变量做因变量,即a个函数。
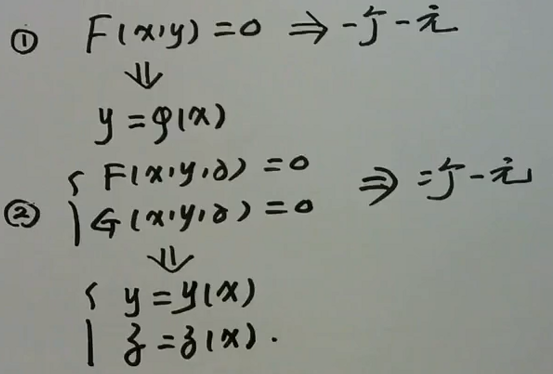
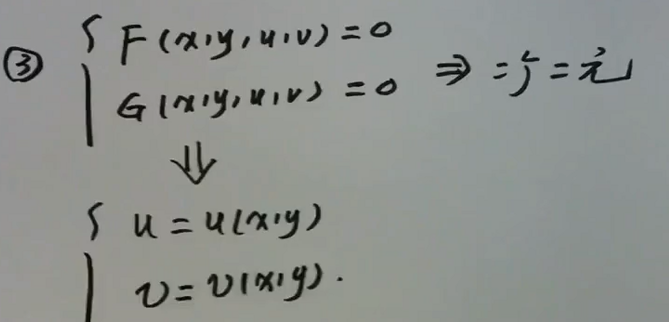
方法1:复合函数求导法求隐函数偏导
求对方程组求偏导时,记住哪些变量是自变量,哪些变量是函数,按复合函数求偏导方法求解即可。
方法2:公式法求隐函数偏导
其实就是将复合函数求导法求隐函数的偏导数的过程,总结成了公式。
隐函数存在定理 1(两个变量的隐函数求偏导) 设函数 \(F(x, y)\) 在点 \(P\left(x_{0}, y_{0}\right)\) 的某一邻域内具有连续 偏导数,且隐函数\(F\left(x_{0}, y_{0}\right)=0, F_{y}\left(x_{0}, y_{0}\right) \neq 0\), 则方程 \(F(x, y)=0\) 在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻域内恒能唯一确定一个连续且具有连续导数的函数 \(y=f(x),\) 它满足条件 \(y_{0}=f\left(x_{0}\right)\), 并有\(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{F_{x}}{F_y}\) (可以用多元复合函数求导法简单推导)
如果函数 \(F(x, y)\) 在点 \(P\left(x_{0}, y_{0}\right)\) 的某一邻域内具有连续 二阶偏导数,可利用复合函数求导法,再求一次导: \(\begin{aligned} \frac{\mathrm{d}^{2} y}{\mathrm{d} x^{2}} &=\frac{\partial}{\partial x}\left(-\frac{F_{x}}{F_{y}}\right)+\frac{\partial}{\partial y}\left(-\frac{F_{x}}{F_{y}}\right) \frac{\mathrm{d} y}{\mathrm{d} x} \\ &=-\frac{F_{x x} F_{y}-F_{y x} F_{x}}{F^{2}}-\frac{F_{x y} F,-F_{yy} F_{x}}{F_{y}^{2}}\left(-\frac{F_{x}}{F}\right) \\ &=-\frac{F_{xx} F_{y}^{2}-2 F_{x y} F_{x} F_{y}+F_{yy} F_{x}^{2}}{F_{y}^{3}}\end{aligned}\)
隐函数存在定理 2 (三个变量的隐函数求偏导)设函数 \(F(x, y, z)\) 在点 \(P\left(x_{0}, y_{0}, z_{0}\right)\) 的某一邻域具有连续偏导数,且隐函数 \(F\left(x_{0}, y_{0}, z_{0}\right)=0, F_{z}\left(x_{0}, y_{0}, z_{0}\right) \neq 0,\) 则方程 \(F(x, y, z)=0\) 在 点\(\left(x_{0}, y_{0}, z_{0}\right)\) 的某一邻域 内恒能唯一确 定一个连 续且具有连 续偏导数的函数 \(z=\) \(f(x, y),\) 它满足条件 \(z_{0}=f\left(x_{0}, y_{0}\right),\) 并有 \(\frac{\partial z}{\partial x}=-\frac{F_{x}}{F_{z}}, \frac{\partial z}{\partial y}=-\frac{F_{y}}{F_{z}}\)
隐函数存在定理 3 (4个变量2个约束的方程组求偏导)\(\quad\) 设 \(F(x, y, u, v), G(x, y, u, v)\) 在点 \(P\left(x_{0}, y_{0}, u_{0}, v_{0}\right)\) 的某一邻域内具有对各个变量的连续偏导数,又 \(F\left(x_{0}, y_{0}, u_{0}, v_{0}\right)=0, G\left(x_{0}, y_{0}, u_{0}, v_{0}\right)=0\), 且偏导数所组成的函数行列式(或称雅可比 ( Jacobi) 式)\(J=\frac{\partial(F, G)}{\partial(u, v)}=\left|\begin{array}{ll} \frac{\partial F}{\partial u} & \frac{\partial F}{\partial v} \\ \frac{\partial G}{\partial u} & \frac{\partial G}{\partial v} \end{array}\right|\)在点 \(P\left(x_{0}, y_{0}, u_{0}, v_{0}\right)\) 不等于零, 则方程 组 \(F(x, y, u, v)=0, G(x, y, u, v)=0\) 在\(\left(x_{0}, y_{0}, u_{0}, v_{0}\right)\) 的某一邻域 内恒能唯一确定一组 连续且具有连 续偏导数的函数\(u=u(x, y), v=v(x, y),\) 它们满足条件 \(u_{0}=u\left(x_{0}, y_{0}\right), v_{0}=v\left(x_{0}, y_{0}\right),\) 并有: \(\frac{\partial u}{\partial x}=-\frac{1}{J} \frac{\partial(F, G)}{\partial(x, v)}=-\frac{\left|\begin{array}{ll}F_{x} & F_{v} \\ G_{x} & G_{v}\end{array}\right|}{\left|\begin{array}{ll}F_{u} & F_{v} \\ G_{u} & G_{v}\end{array}\right|}\) \(\frac{\partial v}{\partial x}=-\frac{1}{J} \frac{\partial(F, G)}{\partial(u, x)}=-\frac{\left|\begin{array}{ll}F_{u} & F_{x} \\ G_{u} & G_{x}\end{array}\right|}{\left|\begin{array}{ll}F_{u} & F_{v} \\ G_{u} & G_{v}\end{array}\right|}\) \(\frac{\partial u}{\partial y}=-\frac{1}{J} \frac{\partial(F, G)}{\partial(y, v)}=-\frac{\left|\begin{array}{ll}F_{y} & F_{v} \\ G_{y} & G_{v}\end{array}\right|}{\left|\begin{array}{ll}F_{u} & F_{v} \\ G_{u} & G_{v}\end{array}\right|}\) \(\frac{\partial v}{\partial y}=-\frac{1}{J} \frac{\partial(F, G)}{\partial(u, y)}=-\frac{\left|\begin{array}{ll}F_{u} & F_{y} \\ G_{u} & G_{y}\end{array}\right|}{\left|\begin{array}{ll}F_{u} & F_{v} \\ G_{u} & G_{v}\end{array}\right|}\) (以上是对方程组各自由变量求偏导,用线性代数的方法解方程组得来的。)
| 一阶偏导数 | 二阶偏导数 | |
|---|---|---|
| 2个变量的隐函数(1个约束)求偏导 | \(\frac{\mathrm{d} y}{\mathrm{d} x}=-\frac{F_{x}}{F_y}\) | \(\begin{aligned} \frac{\mathrm{d}^{2} y}{\mathrm{d} x^{2}} &=\frac{\partial}{\partial x}\left(-\frac{F_{x}}{F_{y}}\right)+\frac{\partial}{\partial y}\left(-\frac{F_{x}}{F_{y}}\right) \frac{\mathrm{d} y}{\mathrm{d} x} \\ &=-\frac{F_{xx} F_{y}^{2}-2 F_{x y} F_{x} F_{y}+F_{yy} F_{x}^{2}}{F_{y}^{3}}\end{aligned}\) |
| 3个变量的隐函数(1个约束)求偏导 | \(\frac{\partial z}{\partial x}=-\frac{F_{x}}{F_{z}}, \frac{\partial z}{\partial y}=-\frac{F_{y}}{F_{z}}\) | |
| 4个变量2个约束的方程组求偏导 | 方程组的行列式解 |
全微分
设函数 \(z=f(x, y)\) 在点 \(P\left(x_{0}, y_{0}\right)\) 的某邻域内有定义,给 \(x, y\) 在 \(x_{0}, y_{0}\) 处分别以增量 \(\Delta x\),\(\Delta y,\) 相应地得到函数的全增量 \(\Delta z,\) 若全增量可表示为\(\Delta z=A \Delta x+B \Delta y+o(\rho)\),其中 \(A, B\) 与 \(\Delta x, \Delta y\) 无关, \(\rho=\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}, o(\rho)\) 为 \(\Delta x \rightarrow 0, \Delta y \rightarrow 0\) 时 \(\rho\) 的高阶无穷小,则称函数 \(f(x, y)\) 在 \(P\left(x_{0}, y_{0}\right)\) 可微, \(A \Delta x+B \Delta y\) 称为 \(f(x, y)\) 在 \(P\left(x_{0}, y_{0}\right)\) 处的全微分 记为\(\left.\mathrm{d} z\right|_{x_{0}, y_{0}}=\mathrm{d} f\left(x_{0}, y_{0}\right)=A \Delta x+B \Delta y\)
| 可微的定义 | 一元函数 | 多元函数(二元函数为例) |
|---|---|---|
| 前提 | 如果函数y=f(x)在点x处的某邻域内有定义, | 设函数 \(z=f(x, y)\) 在点 \(P\left(x_{0}, y_{0}\right)\) 的某邻域内有定义, |
| 全增量 | \(\Delta y\)是函数的增量: \(\Delta y = f(x_0 + \Delta x) -f(x_0)\) | 给 \(x, y\) 在 \(x_{0}, y_{0}\) 处分别以增量 \(\Delta x\),\(\Delta y,\) 相应地得到函数的全增量 \(\Delta z\) : \(\Delta z = f(x_0 + \Delta x, y_0 + \Delta y) -f(x_0, y_0)\) |
| 可微 | 若有\(\Delta y=A \Delta x+o(\Delta x)\), 称y=f(x)在x处可微, 称\(d y=d f(x)=A \Delta x\)为f(x)在x处的微分。 | 若全增量可表示为\(\Delta z=A \Delta x+B \Delta y+o(\rho)\), 其中 \(A, B\) 与 \(\Delta x, \Delta y\) 无关, \(\rho=\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}, o(\rho)\) 为 \(\Delta x \rightarrow 0, \Delta y \rightarrow 0\) 时 \(\rho\) 的高阶无穷小, 则称函数 \(f(x, y)\) 在 \(P\left(x_{0}, y_{0}\right)\) 可微, |
| (全)微分 | 又\(f^{\prime}(x)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=A\),记\(d x=\Delta x\),则微分又可以写成\(\mathrm{d} y=f^{\prime}(x) \mathrm{d} x\) | \(A \Delta x+B \Delta y\) 称为 \(f(x, y)\) 在 \(P\left(x_{0}, y_{0}\right)\) 处的全微分,记为\(\left.\mathrm{d} z\right|_{x_{0}, y_{0}}=\mathrm{d} f\left(x_{0}, y_{0}\right)=A \Delta x+B \Delta y\) \(= f_x^\prime(x_0,y_0)dx +f_y^\prime(x_0,y_0)dy\) |
| 可微与连续、可导的关系 | 一元函数 | 多元函数 |
|---|---|---|
| 可微与连续性的关系 | 可微\(\Rightarrow\)连续 | 可微\(\Rightarrow\)连续 |
| 可微与可导的关系 | 可微\(\Leftrightarrow\) 可导 | 可微\(\Rightarrow\) 可偏导 |
| 可微的充分条件 | 与可导互为充要条件 | 有连续偏导数(各偏导数都连续)\(\Rightarrow\)可微 |
可用多元函数连续的定义证明可微必连续(可微\(\Rightarrow\) 连续)
定理 (可微的必要条件) 如果函数 \(z=f(x, y)\) 在点 \((x, y)\) 可微分,那么该函数在点\((x, y)\) 的偏导数 \(\frac{\partial z}{\partial x}\) 与 \(\frac{\partial z}{\partial y}\) 必定存在 \(,\) 且函数 \(z=f(x, y)\) 在点 \((x, y)\) 的全微分为\(\mathrm{d} z=\frac{\partial z}{\partial x} \Delta x+\frac{\partial z}{\partial y} \Delta y\) (可微\(\Rightarrow\) 可偏导)
注意,(以二元函数为例)某函数的各个偏导数 \(\frac{\partial z}{\partial x}\) 与 \(\frac{\partial z}{\partial y}\) 都存在,函数的微分不一定能写成\(\mathrm{d} z=\frac{\partial z}{\partial x} \Delta x+\frac{\partial z}{\partial y} \Delta y\)。因为不保证剩余部分是广义距离\(\rho\)的高阶无穷小。(同济第七版P73有举例说明)
定理 (可微的充分条件) 如果函数 \(z=f(x, y)\) 的偏导数 \(\frac{\partial z}{\partial x}, \frac{\partial z}{\partial y}\) 在点 \((x, y)\) 连续,那么函数在该点可微分。(连续可偏导\(\Rightarrow\) 可微)
全微分形式不变性
设函数 \(z=f(u, v)\) 具有连续偏导数,则有全微分\(\mathrm{d} z=\frac{\partial z}{\partial u} \mathrm{d} u+\frac{\partial z}{\partial v} \mathrm{d} v\), 又\(u=\varphi(x, y), v=\psi(x, y)\)也又连续的偏导数, 则复合函数\(z=f[\varphi(x, y), \psi(x, y)]\)的全微分为\(\mathrm{d} z=\frac{\partial z}{\partial x} \mathrm{d} x+\frac{\partial z}{\partial y} \mathrm{d} y\), 即\(\begin{aligned} \mathrm{d} z &=\left(\frac{\partial z}{\partial u} \frac{\partial u}{\partial x}+\frac{\partial z}{\partial v} \frac{\partial v}{\partial x}\right) \mathrm{d} x+\left(\frac{\partial z}{\partial u} \frac{\partial u}{\partial y}+\frac{\partial z}{\partial v} \frac{\partial v}{\partial y}\right) \mathrm{d} y \\ &=\frac{\partial z}{\partial u}\left(\frac{\partial u}{\partial x} \mathrm{d} x+\frac{\partial u}{\partial y} \mathrm{d} y\right)+\frac{\partial z}{\partial v}\left(\frac{\partial v}{\partial x} \mathrm{d} x+\frac{\partial v}{\partial y} \mathrm{d} y\right) \\ &=\frac{\partial z}{\partial u} \mathrm{d} u+\frac{\partial z}{\partial v} \mathrm{d} v \end{aligned}\) 可见,无论是u和v作自变量还是x和y作自变量,函数f的全微分形式是一样的,这个性质叫做全微分形式不变性。
二元函数的泰勒公式
定理 \(\quad\) 设 \(z=f(x, y)\) 在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻域内连续且有 \((n+1)\) 阶连续偏导数, \(\left(x_{0}+h, y_{0}+k\right)\) 为此邻域内任一点 , 则有: \(f\left(x_{0}+h, y_{0}+k\right)\) \(=f\left(x_{0}, y_{0}\right)+\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right) f\left(x_{0}, y_{0}\right)+\) \(\frac{1}{2 !}\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{2} f\left(x_{0}, y_{0}\right)+\cdots+\frac{1}{n !}\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{n} f\left(x_{0}, y_{0}\right)+\) \(\frac{1}{(n+1) !}\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{n+1} f\left(x_{0}+\theta h, y_{0}+\theta k\right) \quad(0<\theta<1)\) ,称为带皮亚诺余项的二元函数泰勒公式。其中记号 \(\begin{array}{l} \left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right) f\left(x_{0}, y_{0}\right) \text { 表示 } h f_{x}\left(x_{0}, y_{0}\right)+k f_{y}\left(x_{0}, y_{0}\right) \\ \left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{2} f\left(x_{0}, y_{0}\right) \text { 表示} h^{2} f_{x x}\left(x_{0}, y_{0}\right)+2 h k f_{x y}\left(x_{0}, y_{0}\right)+k^{2} f_{y y}\left(x_{0}, y_{0}\right) \end{array}\) 一般 地,记号\(\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{m} f\left(x_{0}, y_{0}\right) \text { 表示 }\left. \sum_{p=0}^{m} C_{m}^{p} h^{p} k^{m-p} \frac{\partial^{m} f}{\partial x^{p} \partial y^{m-p}}\right|_{\left(x_{0} \cdot y_{0}\right)}\)
相同情况下,也可以写成带拉格朗日余项的二元函数泰勒公式: 设 \(z=f(x, y)\) 在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻域内连续且有 \((n+1)\) 阶连续偏导数, \(\left(x_{0}+h, y_{0}+k\right)\) 为此邻域内任一点 , 则有: \(f\left(x_{0}+h, y_{0}+k\right)\) \(=f\left(x_{0}, y_{0}\right)+\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right) f\left(x_{0}, y_{0}\right)+\frac{1}{2 !}\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{2} f\left(x_{0}, y_{0}\right)+\cdots+\frac{1}{n !}\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{n} f\left(x_{0}, y_{0}\right)+R_{n}\) 其中\(R_{n}=\frac{1}{(n+1) !}\left(h \frac{\partial}{\partial x}+k \frac{\partial}{\partial y}\right)^{n+1} f\left(x_{0}+\theta h, y_{0}+\theta k\right) \quad(0<\theta<1)\),是拉格朗日余项。
由二元函数的泰勒公式可知 ,右端的 h 及 \(k\) 的 \(n\) 次多项式部分 近似表 达函数 $f(x_{0}+h, y_{0}+k) $ 时,其误差为 $ R_{n} $. 由假设, 函数的各 \((n+1)\) 阶偏导数都 连续,故它们的绝对值在点 \(\left(x_{0}, y_{0}\right)\) 的某一邻城内都不超过某一正常数 M. 于是,有下面的误差估计式: \(\begin{aligned}\left|R_{n}\right| & \leqslant \frac{M}{(n+1) !}(|h|+|k|)^{n+1}=\frac{M}{(n+1) !} \rho^{n+1}\left(\frac{|h|}{\rho}+\frac{|k|}{\rho}\right)^{n+1} \\ & \leqslant \frac{M}{(n+1) !}(\sqrt{2})^{n+1} \rho^{n+1} \end{aligned}\) 其中 \(\rho=\sqrt{h^{2}+k^{2}}\) 即,误差 \(|R_{n}|\) 是当 \(\rho \rightarrow 0\) 时比 \(\rho^{n}\) 高阶的无穷小
对于n=0,泰勒公式变成 \(f\left(x_{0}+h, y_{0}+k\right)\) \(=f\left(x_{0}, y_{0}\right)+h f_{x}\left(x_{0}+\theta h, y_{0}+\theta k\right)+k f_{y}\left(x_{0}+\theta h, y_{0}+\theta k\right)\) 称为二元函数的拉格朗日中值定理。