高等数学-多元微积分-曲线积分与曲面积分
高等数学-多元微积分-曲线积分与曲面积分
定积分的积分范围是数轴上的一个区间(线状); 二重积分的积分范围是平面内的一个闭区域(面状); 三重积分的积分范围是空间内的一个闭区域(体状); 本章将积分范围推广到平面以及空间内的一段曲线弧(曲线积分); 还将积分范围推广到空间内的一片曲面(曲面积分);
| 积分域 | 积分号 | 举例 |
|---|---|---|
| 线状 | \(\int\) | 定积分\(\int_a^b f(x)dx\) 曲线积分\(\int_L\) |
| 面状 | \(\iint\) | 二重积分\(\iint_D f(x,y) d\sigma\) 曲面积分\(\iint_\Sigma\) |
| 体状 | \(\iiint\) | 三重积分\(\iiint_\Omega f(x,y,z) dv\) |
研究/学习过程: 研究背景 -> 抽象(积分种类) -> 性质 -> 计算 -> 应用
对弧长的曲线积分(第一类曲线积分)
背景
空间曲线的质量问题
元素法: \(\forall ds \in L\) \(dm = \rho(x,y)ds\) \(m=\int_L dm = \int_L \rho(x,y) ds\)
这里积分是在L上积分,不是上下限; 这里是\(ds\)不是\(dx\); 所以这是一种新的积分类型
抽象(对弧长的曲线积分概念)
\(\int_L f(x,y)ds\)称为\(f(x,y)\)在平面内的曲线段L上对弧长的曲线积分。 \(\int_L f(x,y,z)ds\)称为\(f(x,y,z)\)在空间曲线段L上对弧长的曲线积分。
性质
积分的加减 = 加减的积分
常数可以提出来
\(L = L_1 + L_2\)则可以分段积分
积分的绝对值小于等于绝对值的积分
奇偶性对称性: 1)如果曲线段L关于y轴对称/左右对称(并记右半段为\(L_1\)) 若\(f(-x,y) = -f(x,y)\),则\(\int_L f(x,y) ds = 0\) 若\(f(-x,y) = f(x,y)\),则\(\int_L f(x,y) ds = 2 \int_{L_1} f(x,y) ds\)
2)如果曲线段L关于x轴对称/上下对称(并记上半段为\(L_1\)) 若\(f(x,-y) = -f(x,y)\),则\(\int_L f(x,y) ds = 0\) 若\(f(x,-y) = f(x,y)\),则\(\int_L f(x,y) ds = 2 \int_{L_1} f(x,y) ds\)
3)如果曲线段L关于\(y=x\)对称, 则\(\int_L f(x,y) ds = \int_{L} f(y,x) ds\)
计算法
替代法
不一定有用。
定积分法
平面内对弧长的曲线积分:
1)用直角坐标表示曲线段L的方程:\(y=\varphi(x) \quad (a \le x \le b)\) \(\int_L f(x,y) ds = \int_a^b f[x, \varphi(x)] \sqrt{1+ \varphi^{\prime 2} (x)} dx\)
2)用参数方程表示曲线段L:\(\left\{\begin{array}{} x=\varphi(t) \\ y =\psi(t)\end{array}\right. \quad (\alpha \le t \le \beta)\) \(\int_L f(x,y) ds = \int_\alpha^\beta f[\varphi(t), \psi(t)] \sqrt{\varphi^{\prime 2} (t) + \psi^{\prime 2}(t)} dt\) (对弧长的曲线积分中\(\alpha\)必小于等于\(\beta\),这是因为\(ds\)必为正)
3)用极坐标表示曲线L的方程:\(\rho = \rho(\theta) \quad (\theta_1 \le \theta \le \theta_2)\) \(\int_L f(x,y) ds = \int_{\theta_1}^{\theta_2} f[\rho(\theta), \theta] \sqrt{\rho^2(\theta) + \rho^{\prime 2}(\theta)}d\theta\)
我们可以很容易地推广到空间中对弧长的曲线积分:
1)用参数方程表示空间曲线段L的方程:\(\left\{\begin{array}{} x=\varphi(t) \\ y =\psi(t) \\ z = \omega(t) \end{array}\right. \quad (\alpha \le t \le \beta)\) \(\int_L f(x,y,z) ds = \int_\alpha^\beta f[\varphi(x), \psi(y), \omega(t)] \sqrt{\varphi^{\prime 2} (t) + \psi^{\prime 2}(t) + \omega^{\prime 2}(t)} dt\)
对坐标的曲线积分(第二类曲线积分)
背景
变力在曲线上的做功问题
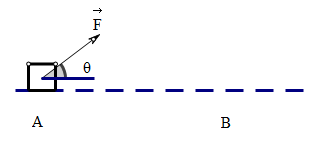 (一维)双理想情况(做功路径是直的、力是恒力): \(W = |\vec{F}| \cos \theta \cdot |\vec{AB} | = \vec{F} \cdot \vec{AB}\)
(一维)双理想情况(做功路径是直的、力是恒力): \(W = |\vec{F}| \cos \theta \cdot |\vec{AB} | = \vec{F} \cdot \vec{AB}\)
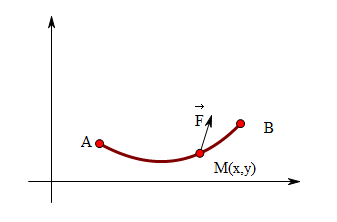 (二维)双不理想情况(做功路径是曲线、力不是恒力): 设\(\vec{F} = \{P(x,y), Q(x,y)\}\),用元素法分析: \(\forall \vec{ds} \in L, \vec{ds} = \{dx, dy\}\), 注意这里的曲线段以及曲线段L以及曲线段的微元都是有方向的。 \(dw = \vec{F} \cdot \vec{ds} = (P,Q) \cdot (dx, dy) = P(x,y)dx + Q(x,y)dy\) \(W = \int_L dw = \int_L P(x,y)dx + Q(x,y)dy\)
(二维)双不理想情况(做功路径是曲线、力不是恒力): 设\(\vec{F} = \{P(x,y), Q(x,y)\}\),用元素法分析: \(\forall \vec{ds} \in L, \vec{ds} = \{dx, dy\}\), 注意这里的曲线段以及曲线段L以及曲线段的微元都是有方向的。 \(dw = \vec{F} \cdot \vec{ds} = (P,Q) \cdot (dx, dy) = P(x,y)dx + Q(x,y)dy\) \(W = \int_L dw = \int_L P(x,y)dx + Q(x,y)dy\)
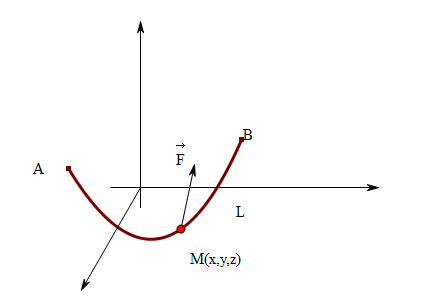 (三维)双不理想情况(做功路径是曲线、力不是恒力): 设\(\vec{F} = \{P(x,y,z), Q(x,y,z), R(x,y,z)\}\),用元素法分析: \(\forall \vec{ds} \in L, \vec{ds} = \{dx, dy, dz\}\), 注意这里的曲线段以及曲线段L以及曲线段的微元都是有方向的。 \(dw = \vec{F} \cdot \vec{ds} = (P,Q,R) \cdot (dx, dy, dz) = P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz\) \(W = \int_L dw = \int_L P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z) dz\)
(三维)双不理想情况(做功路径是曲线、力不是恒力): 设\(\vec{F} = \{P(x,y,z), Q(x,y,z), R(x,y,z)\}\),用元素法分析: \(\forall \vec{ds} \in L, \vec{ds} = \{dx, dy, dz\}\), 注意这里的曲线段以及曲线段L以及曲线段的微元都是有方向的。 \(dw = \vec{F} \cdot \vec{ds} = (P,Q,R) \cdot (dx, dy, dz) = P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz\) \(W = \int_L dw = \int_L P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z) dz\)
抽象(对坐标的曲线积分概念)
对于二维平面中的\(\int_L P(x,y)dx + Q(x,y)dy\), \(\int_L P(x,y)dx\)称为\(P(x,y)\)在有向曲线段L上对坐标的曲线积分; \(\int_L Q(x,y)dx\)称为\(Q(x,y)\)在有向曲线段L上对坐标的曲线积分.
对于三维空间中的\(\int_L P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz\), \(\int_L P(x,y,z)dx\)称为\(P(x,y,z)\)在有向曲线段L上对坐标的曲线积分; \(\int_L Q(x,y,z)dx\)称为\(Q(x,y,z)\)在有向曲线段L上对坐标的曲线积分; \(\int_L R(x,y,z)dx\)称为\(R(x,y,z)\)在有向曲线段L上对坐标的曲线积分.
性质
积分的加减 = 加减的积分
常数可以提出来
\(L = L_1 + L_2\)则可以分段积分
\(\int_{L^-} = - \int _L\),即有向曲线段取相反方向,(对坐标的曲线)积分结果也取反。
对坐标的曲线积分可以转化为对弧长的曲线积分/第二类曲线积分可以转换为第一类曲线积分: \(\int_L P(x,y)dx + Q(x,y)dy \\= \int_L P(\varphi(t),\psi(t))\varphi^\prime(t)dt + Q(\varphi(t),\psi(t))\psi^\prime(t)dt \\= \int_L P[\varphi(t),\psi(t)]\frac{\varphi^\prime(t)}{\sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)}} \cdot\sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)}dt + Q[\varphi(t),\psi(t)]\frac{\psi^\prime(t)}{\sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)}}\cdot \sqrt{\varphi^{\prime 2}(t) + \psi^{\prime 2}(t)}dt \\ =\int_L P(x,y) \cos \alpha ds + Q(x,y)\cos\beta ds \\ = \int_L (P,Q)\cdot (\cos\alpha ,\cos\beta) ds \\= \int_L \vec{A} \cdot \vec{e_n} ds\)
计算法
定积分法
1)用直角坐标表示有向曲线段L的方程:\(y = \varphi(x)\) (起点\(x=a\),终点\(x=b\)) 则二维平面内\(\int_L P(x,y)dx + Q(x,y)dy = \int_a^b P[x,\varphi(x)]dx + Q[x,\varphi(x)]\varphi^\prime(x)dx\) 三维类似。
2)由参数方程表示有向曲线段L:\(\left\{\begin{array}{} x=\varphi(t) \\ y =\psi(t)\end{array}\right.\), (起点\(t=\alpha\),终点\(t=\beta\)) 则二维平面内\(\int_L P(x,y)dx + Q(x,y)dy = \int_\alpha^\beta P[\varphi(t),\psi(t)]\varphi^\prime(t)dt + Q[\varphi(t),\psi(t)]\psi^\prime(t)dt\) (这里下限\(\alpha\)要对应有向曲线段的起点) 三维类似。
转化为二重积分法(格林公式/平面的域与界的关系)
首先明确二维平面的域与界的概念与联系公式(格林公式),然后利用格林公式将闭合有向曲线段L上的曲线积分转化为D上的二重积分。
格林公式
当1)D为连通区域, 2)L为D的正项边界, 3)\(P(x,y), Q(x,y)\)在D上连续可偏导, 则有(格林公式): $ _L Pdx + Qdy = _D ( - ) d$
(若不封闭,可补为封闭图形) (若L不是正向的,则积分前补负号时可取L正向) (若是多连通区域,应包含所有边界)
转化为曲面积分法(斯托克斯公式/曲面的域与界的关系)
斯托克斯公式可看作是格林公式的推广,格林公式建立起二维平面上域与界的联系,而斯托克斯公式建立起空间曲面域与界的联系。
这里需要先学习/掌握后面对坐标的曲面积分章节的内容。然后要明确曲面的域与界的概念与联系公式(斯托克斯公式),然后利用斯托克斯公式将闭合有向曲线段L上的曲线积分转化为曲面积分。
斯托克斯公式
定理 设 \(\Gamma\) 为分段光滑的空间有向闭曲线, $ $是以 \(\Gamma\) 为边界的分片光滑 的有向曲面, \(\Gamma\) 的正向与 \(\Sigma\)的侧符合右手规则, 若函数 \(P(x, y, z), Q(x, y, z)\) 与\(R(x, y, z)\) 在曲面 \(\Sigma(\) 连同边界 \(\Gamma)\) 上具有一阶连续偏导数 , 则有(斯托克斯公式): \(\iint_{\Sigma}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \mathrm{d} y \mathrm{d} z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \mathrm{d} z \mathrm{d} x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{d} y\)\(=\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\)
(斯托克斯公式建立起: 曲线积分与曲面积分的联系/界与域的联系)
斯托克斯公式更方便记忆的形式: \(\int_{\Sigma}\left|\begin{array}{ccc}\mathrm{d} y \mathrm{d} z & \mathrm{d} z \mathrm{d} x & \mathrm{d} x \mathrm{d} y \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R\end{array}\right|=\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\)
后面学习了对面积和对坐标的曲面积分的关系后,即\(\vec{dS} = \vec{n}dS =( \cos\alpha, \cos\beta, \cos\gamma) dS\),斯托克斯公式还可写为: \(\int_{\Sigma}\left|\begin{array}{ccc}\cos \alpha & \cos \beta & \cos \gamma \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R\end{array}\right| \mathrm{d} S=\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\)
平面上与路径无关的曲线积分计算法
根据格林公式/平面中域与界的关系 $ _L Pdx + Qdy = _D ( - ) d$可以推出平面中的曲线与积分路径无关的条件(见如下定理)
定理:若: 1)D为单连通区域, 2)\(P(x,y),Q(x,y)\)在D上连续可偏导, 则有如下4个等价结论: 1)$ _L Pdx + Qdy\(与路径无关 2)任意闭曲线\)C D\(,有\) _C Pdx + Qdy= 0$ 3)$ $ (柯西-黎曼条件) 4)\(\exist u(x,y)\)使得\(du = Pdx + Qdy\)。 (即\(\frac{\partial u}{\partial x} = P, \frac{\partial u}{\partial y} = Q\))
上面比较简洁规范的一种结论是$ $ ,它代表了$ _L Pdx + Qdy$与路径无关。
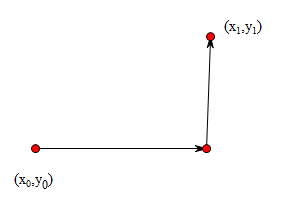 而曲线积分与路径无关时($ \(),又有如下结论: 1)如果\) \(,则\)L Pdx + Qdy ={(x_0,y_0)}^{(x_1,y_1)} Pdx + Qdy = {x_0}^{x_1} P(x,y_0)dx + {y_0}^{y_1} Q(x_1,y)dy$ 2)如果$ \(,且\)Pdx + Qdy = du\(,则\)L Pdx + Qdy = {(x_0,y_0)}^{(x_1,y_1)} du = u(x_1,y_1) - u(x_0,y_0)$ 1)如果$ \(,则\)u(x,y) ={(x_0,y_0)}^{(x,y)} Pdx + Qdy = {x_0}^{x} P(x,y_0)dx + _{y_0}^{y} Q(x,y)dy$
而曲线积分与路径无关时($ \(),又有如下结论: 1)如果\) \(,则\)L Pdx + Qdy ={(x_0,y_0)}^{(x_1,y_1)} Pdx + Qdy = {x_0}^{x_1} P(x,y_0)dx + {y_0}^{y_1} Q(x_1,y)dy$ 2)如果$ \(,且\)Pdx + Qdy = du\(,则\)L Pdx + Qdy = {(x_0,y_0)}^{(x_1,y_1)} du = u(x_1,y_1) - u(x_0,y_0)$ 1)如果$ \(,则\)u(x,y) ={(x_0,y_0)}^{(x,y)} Pdx + Qdy = {x_0}^{x} P(x,y_0)dx + _{y_0}^{y} Q(x,y)dy$
曲线积分基本定理
设 \(\vec{F}(x, y)=P(x, y) \vec{i}+Q(x, y) \vec{j}\) 是平面区 域 \(G\) 内的一个向量场, 若 \(P(x, y)\) 与 \(Q(x, y)\) 都在 \(G\) 内连续, 且存在一个数量函数\(f(x, y),\) 使得 \(\vec{F}=\nabla f,\) 则曲线积分 \(\int_{L} \vec{F} \cdot \mathrm{d} \vec{r}\) 在 \(G\) 内与路径无关, 且\(\int_{L} \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{r}=f(B)-f(A)\)。其中 L 是位于 G 内起点为 A.终点为 B 的任一分段光滑曲线.
| 微积分基本公式 | \(\int_{a}^{b} f(x) \mathrm{d} x=F(b)-F(a)\) | 其中 \(F^{\prime}(x)=f(x)\) |
| 曲线积分基本公式 | \(\int_{L} \boldsymbol{F} \cdot \mathrm{d} \boldsymbol{r}=f(B)-f(A)\) | 其中\(\vec{F}=\nabla f(x,y)\) |
空间中与路径无关的曲线积分计算法
根据斯托克斯公式\(\iint_{\Sigma}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \mathrm{d} y \mathrm{d} z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \mathrm{d} z \mathrm{d} x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{d} y\)\(=\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) 可以推出空间曲线积分与路径无关的条件(见如下定理)
定理 设空间区域 G 是一维单连通域, 若函数 \(P(x, y, z), Q(x, y, z)\) 与\(R(x, y, z)\) 在 \(G\) 内具有一阶连续偏导数, 则: 空间 曲 线 积分 \(\int_{r} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) 在 \(G\)内与路径无关(或沿 G 内任意闭曲线的曲线积分为零)
\(\Leftrightarrow\) \(\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}, \quad \frac{\partial Q}{\partial z}=\frac{\partial R}{\partial y}, \quad \frac{\partial R}{\partial x}=\frac{\partial P}{\partial z}\)在 G 内恒成立. \(\Leftrightarrow\) 表达式 \(P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) 在 \(G\) 内成为某一函数 \(u(x, y, z)\) 的全微分 (同时可求出\(u(x, y, z)=\int_{\left(x_{0}, y_{0}, z_{0}\right)}^{(x, y, z)} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\))
对面积的曲面积分(第一类曲面积分)
背景
空间曲面的质量问题
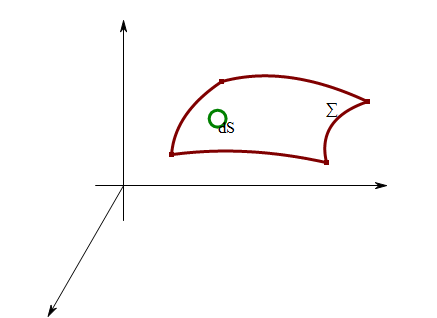
用元素法分析: \(\forall dS \subset \Sigma\) \(dm = \rho(x,y,z) dS\) \(m=\iint_\Sigma dm = \iint_\Sigma \rho(x,y,z) dS\)
这里是对空间曲面\(\Sigma\)积分,不是二重积分中对坐标面上的投影\(D_{xy}\)积分,也不是三重积分中对体积\(\Omega\)的积分; 这里的dS是空间曲面的一小块,也不是二重积分中的面积元素\(d\sigma\); 则这是一种新的积分类型。
抽象(对面积的曲面积分)
\(\iint_\Sigma f(x,y,z) dS\),称为\(f(x,y,z)\)在曲面\(\Sigma\)上的对面积的曲面积分
性质
积分的加减 = 加减的积分
常数可以提出来
\(\Sigma = \Sigma_1 + \Sigma_2\)则可以分块积分
\(\iint_\Sigma dS = A\),即空间曲面的面积
奇偶性对称性: 1)若空间曲面\(\Sigma\)关于xOy平面对称(上下对称)(上半曲面记为\(\Sigma_1\)): 如果\(f(x,y,-z) = -f(x,y,z)\),则\(\iint_\Sigma f dS = 0\); 如果\(f(x,y,-z) = f(x,y,z)\),则\(\iint_\Sigma f dS = 2 \iint_{\Sigma_1} f dS\); 2)若空间曲面\(\Sigma\)关于yOz平面对称(前后对称)。。。 3)若空间曲面\(\Sigma\)关于zOx平面对称(左右对称)。。。 4)若空间曲面\(\Sigma\)关于y=x柱面对称,则\(\iint_\Sigma f(x,y,z) dS = \iint_{\Sigma} f(y,x,z) dS\) 5)若空间曲面\(\Sigma\)关于z=y柱面对称。。。 6)若空间曲面\(\Sigma\)关于z=x柱面对称。。。
计算法
替代法
二重积分法

对于\(\iint_\Sigma f(x,y,z) dS\) 空间曲面\(\Sigma\)表示为\(z=\varphi(x,y)\),其中\((x,y) \in D_{x,y}\) \(dS= \sqrt{1+z_x^{\prime 2} + z_y^{\prime 2}} d\sigma\) \(\iint_\Sigma f(x,y,z) dS = \iint_{D_{xy}} f[x,y,\varphi(x,y)] \sqrt{1+z_x^{\prime 2} + z_y^{\prime 2}} d\sigma\)
对坐标的曲面积分(第二类曲面积分)
背景
流过曲面的流量问题
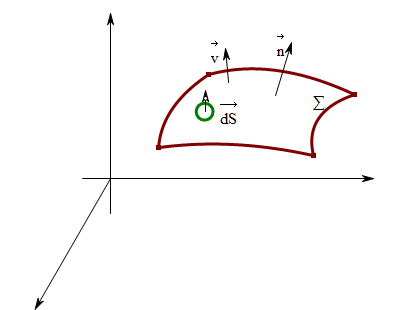 \(\vec{v} = \{P(x,y,z), Q(x,y,z), R(x,y,z)\}\) \(\Sigma\)为有侧曲面(如上图\(\vec{n}\)指明上侧为正) 问单位时间内流入曲面一侧的流量是多少?
\(\vec{v} = \{P(x,y,z), Q(x,y,z), R(x,y,z)\}\) \(\Sigma\)为有侧曲面(如上图\(\vec{n}\)指明上侧为正) 问单位时间内流入曲面一侧的流量是多少?
用元素法分析: \(\forall \vec{dS} \subset \Sigma\),\(\vec{dS}\)的大小表示小面元的面积,方向垂直于小面元(并与曲面\(\Sigma\)同侧)(小面元可看作是平面) 则\(\vec{dS}\)可分解为到三个坐标面的投影(从各坐标轴正向看): \(\vec{dS} = \{dydz,dzdx,dxdy\} = |\vec{dS}| (\cos \alpha, \cos \beta, \cos \gamma)\) (比如\(dydz\)是\(\vec{dS}\)在yOz平面的投影,\(|dydz|\)表示投影面积,\(dydz\)可正可负,且有\(dydz = |\vec{dS}| \cos \alpha\)) 则单位时间内流入曲面上小微元的流量微元: \(d \Phi = \vec{v} \cdot \vec{dS} = Pdydz + Qdzdx + Rdxdy\) 则单位时间内流入曲面侧得流量: \(\Phi = \iint_\Sigma d \Phi = \iint_\Sigma Pdydz + Qdzdx + Rdxdy\)
注意:这里是对空间曲面\(\Sigma\)积分,不是对曲面在坐标轴上的投影\(D_{xy},D_{yz},D_{zx}\)积分(即并不是二重积分),这是一种新的积分类型。
抽象(对坐标的曲面积分的概念)
根据\(\iint_\Sigma Pdydz + Qdzdx + Rdxdy\)
我们把$ _Pdydz\(称为\)P(x,y,z)\(在有侧曲面\)$上对坐标y,z的曲面积分。
性质
积分的加减 = 加减的积分
常数可以提出来
\(\Sigma = \Sigma_1 + \Sigma_2\)则可以分块积分
\(\iint_{\Sigma^-} = -\iint_\Sigma\)
\(\iint_\Sigma Pdydz + Qdzdx + Rdxdy = \iint_\Sigma (P\cos\alpha + Q\cos\beta + R\cos\gamma) dS\),即对坐标的曲面积分可以转化为对面积的曲面积分/第二类曲面积分可转化为第一类曲面积分
计算法
二重积分法
 对于\(\iint_\Sigma R(x,y,z)dxdy\) 将曲面\(\Sigma\)表示为\(z=\varphi(x,y)\), 其中\((x,y) \in D_{xy}\) 则\(\iint_\Sigma R(x,y,z)dxdy = \pm \iint_{D_{xy}} R(x,y,z)dxdy\) 其中当\(\cos\gamma>0\)或者\(\Sigma\)取上侧时,\("\pm"\)取”+“ 其中当\(\cos\gamma<0\)或者\(\Sigma\)取下侧时,\("\pm"\)取”-“
对于\(\iint_\Sigma R(x,y,z)dxdy\) 将曲面\(\Sigma\)表示为\(z=\varphi(x,y)\), 其中\((x,y) \in D_{xy}\) 则\(\iint_\Sigma R(x,y,z)dxdy = \pm \iint_{D_{xy}} R(x,y,z)dxdy\) 其中当\(\cos\gamma>0\)或者\(\Sigma\)取上侧时,\("\pm"\)取”+“ 其中当\(\cos\gamma<0\)或者\(\Sigma\)取下侧时,\("\pm"\)取”-“
注意: 对坐标的曲面积分\(\iint_\Sigma R(x,y,z)dxdy\)中,\(dxdy\)表示\(\vec{dS}\)的投影,可正可负; 二重积分\(\iint_{D_{xy}} R(x,y,z)dxdy\)中,\(dxdy\)表示面积元素,必取正。
转化为三重积分法(高斯公式/域与界的关系)
首先明确三维空间的域与界的概念与联系公式(高斯公式),然后利用高斯公式将\(\Sigma\)上的曲面积分转化为几何体\(\Omega\)内的三重积分。
高斯公式
若:1)\(\Omega\)为几何体,\(\Sigma\)为外表面, 2)\(P(x,y,z), Q(x,y,z),R(x,y,z)\)在\(\Omega\)内连续可偏导 则\(\oiint_\Sigma Pdydz + Qdzdx + Rdxdy = \iiint_\Omega \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) dv\)
(若图形不封闭,可补为封闭体) (若取内表面,积分前加负号变为取外表面)
仅与曲面边界有关的曲面积分计算法
仅与曲面边界有关而与曲面内部形状无关的曲面积分,等价于沿任意闭合曲面对坐标的曲面积分为0。
设 \(G\) 是空间二维单连通区域, 若 \(P(x, y, z), Q(x, y, z)\) 与 \(R(x, y, z)\)在 G 内具有一阶连续偏导数, 则: 曲面积分\(\iint_{\Sigma} P \mathrm{d} y \mathrm{d} z+Q \mathrm{d} z \mathrm{d} x+R \mathrm{d} x \mathrm{d} y\)在G 内与所取曲面 \(\Sigma\) 无关而只取决于 \(\Sigma\) 的边界曲线(或沿 \(G\) 内任一闭曲面的曲面积分为零) \(\Leftrightarrow\) \(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=0\)在 G 内恒成立. (由高斯公式可证左至右,反证法可证右至左)
对于这样的曲面积分,在保证曲面边界不变的情况下,可以选取最简单/方便计算的曲面来计算。
物理应用
通量
我们从前面知道,对坐标的曲面积分的起源/背景是流量问题,即单位时间内通过曲面侧的流量。
在物理中,根据其物理意义,把对各个坐标的曲面积分的合并形式\(\iint_\Sigma Pdydz + Qdzdx + Rdxdy= \iint_{\Sigma} \vec{A} \cdot \vec{n} \mathrm{d} S\)定义为通量: 设有向量场\(\boldsymbol{A}(x, y, z)=P(x, y, z) \boldsymbol i+Q(x, y, z) \boldsymbol{j}+R(x, y, z) \boldsymbol{k}\), 其中函数 P ,Q 与 R 均具有一阶连续偏导数, \(\Sigma\) 是场内的一片有向曲面, \(\vec{n}\) 是 \(\Sigma\)在点( \(x, y, z)\) 处的单位法向量, 则积分\(\iint_{\Sigma} \vec{A} \cdot \vec{n} \mathrm{d} S\)称为向量场 \(\vec{A}\) 通过曲面 \(\Sigma\) 向着指定侧的通量(或流量)
即物理问题中的通量,就是数学中的对坐标的曲面积分。
散度
高斯公式给出了空间几何体的域和界的关系:\(\oiint_\Sigma Pdydz + Qdzdx + Rdxdy = \iiint_\Omega \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) dv\) 这里\(\vec{v} = P\vec{j}+Q\vec{j}+R\vec{k}\)
考虑其物理意义: 高斯公式左边:\(\iint_\Sigma Pdydz + Qdzdx + Rdxdy= \iint_{\Sigma} \vec{v} \cdot \vec{n} \mathrm{d} S= \iint_{\Sigma} v_n \mathrm{d} S\) 表示流体的通量:向量场 \(\vec{A}\) 通过曲面 \(\Sigma\) 向着指定侧的通量(或流量), 若流体不可压缩的情况下,流出的量应当全部由内部产生。 则高斯公式右边:\(\iiint_\Omega \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) dv\) 应当表示在空间\(\Omega\)内,单位时间内产生的的流体总量。
我们用\(\Omega\)的体积V去除高斯公式两边: \(\frac{1}{V} \oiint_{\Sigma} v_{n} \mathrm{d} S=\frac{1}{V} \iiint_{\Omega}\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) \mathrm{d} v\), 这表示\(\Omega\) 内的源头在单位时间单位体积内所产生的流体质量的平均值. 再根据积分中值定理,去掉右边的积分号: \(\frac{1}{V} \oiint_{\Sigma} v_{n} \mathrm{d} S=\left.\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)\right|_{(\xi, \eta, \zeta)}\) 并令\(\Omega\)缩向一点\(M(x,y,z)\)得: \(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=\lim _{\Omega \rightarrow M} \frac{1}{V} \oiint_{\Sigma} v_{n} \mathrm{d} S\) 则\(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\)表示速度场 \(\vec{v}\)在点 M 的通量密度/流量密度或散度(流量产生密度),可看做稳定流动的不可压缩流体在点 M 的源头强度.
记为\(\operatorname{div} \vec{v}(M)=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}=\nabla \cdot \boldsymbol{v}\)
则高斯公式也可以写成如下形式: \(\iint_{\Omega} \operatorname{div} \boldsymbol{A} \mathrm{d} v=\iint_{\Sigma} A_{n} \mathrm{d} S\) \(\iiint_{\Omega} \nabla \cdot \boldsymbol{A} \mathrm{d} v=\iint_{\Sigma} A_{n} \mathrm{d} S\)
环流量
设有向量场\(\boldsymbol{A}(x, y, z)=P(x, y, z)\boldsymbol{i}+Q(x, y, z) \boldsymbol{j}+R(x, y, z) \boldsymbol{k}\), 其中函数 P.Q 与 R 均连续, \(\Gamma\) 是 A 的定义域内的一条分段光滑的有向闭曲线 , \(\tau\)是 \(\Gamma\) 在点 \((x, y, z)\) 处的单位切向量, 则积分\(\oint_{\Gamma} \boldsymbol{A} \cdot \boldsymbol{\tau} \mathrm{d} s=\oint_{\Gamma} \boldsymbol{A} \cdot \mathrm{d} \boldsymbol{r}=\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\)称为向量场$ $ 沿有向闭曲线 \(\Gamma\) 的环流量. 这体现了向量场沿闭合曲线\(\Gamma\)轨迹的积累。
即物理问题中的环流量,就是数学中的对坐标的曲线积分。
旋度
斯托克斯公式给出了空间曲面上域和界的关系: \(\iint_{\Sigma}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \mathrm{d} y \mathrm{d} z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \mathrm{d} z \mathrm{d} x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{d} y\)\(=\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\)
类似于向量场\(\vec{A}\)的通量可以引出向量场\(\vec{A}\)在某一点处的通量密度/散度一样, 通过向量场\(\vec{A}\)的环流量可以引出向量场\(\vec{A}\)在某一点出的旋度概念:
我们用空间曲面\(\Sigma\)的面积S去除斯托克斯公式两边: \(\frac{1}{S}\iint_{\Sigma}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \mathrm{d} y \mathrm{d} z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \mathrm{d} z \mathrm{d} x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{d} y\)\(=\frac{1}{S}\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) 根据两种曲面积分的关系,变为: \(\frac{1}{S}\iint_{\Sigma}\left[\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \cos\alpha+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \cos\beta+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \cos\gamma\right] dS\)\(=\frac{1}{S}\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) 等式右边反映了单位面积上,向量场沿闭合曲线\(\Gamma\)轨迹的积累。 再根据积分中值定理,去掉左边的积分号: \(\left.\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \cos\alpha+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \cos\beta+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \cos\gamma\right|_{(\xi, \eta, \zeta)}\)\(=\frac{1}{S}\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) 并令曲面\(\Sigma\)缩向一点\(M(x,y,z)\)得: \(\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z},\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x},\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\cdot (\cos\alpha,\cos\beta, \cos\gamma)=\lim _{\Sigma \rightarrow M} \frac{1}{S}\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) 等式右边反映了向量场沿某点附近的闭合曲线\(\Gamma\)轨迹的积累。 那么等式左边也反映了向量场沿某点附近的闭合曲线\(\Gamma\)轨迹的积累。 我们可以取等式左边除方向余弦外的部分来表征向量场沿某点附近的闭合曲线\(\Gamma\)轨迹的积累:(将其定义为旋度)\(\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\boldsymbol i+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\boldsymbol j+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \boldsymbol{k}\)
记为: \(\operatorname{rot} \vec{A}=\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\boldsymbol i+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\boldsymbol j+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \boldsymbol{k} \\=\nabla \times \vec{A} \\=\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{array}\right|\)
附录
附录1:域与界的概念与联系公式
二维平面内的域与界
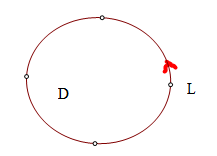 单连通区域D,边界曲线L(有向:逆时针正,顺时针负)
单连通区域D,边界曲线L(有向:逆时针正,顺时针负)
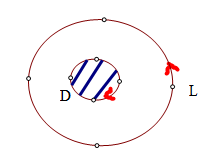 多连通区域D,边界曲线L(有向:外逆内顺位正方向)
多连通区域D,边界曲线L(有向:外逆内顺位正方向)
三维空间内的域与界
三维空间的域:几何体\(\Omega\) 三维空间的界:几何体的表面(有方向/侧:向外取正)
域与界的联系公式
| 维度 | 域 | 界 | 联系公式 |
|---|---|---|---|
| 一维空间 | [a,b] | 边界为a,b | 牛顿-莱布尼兹公式:\(F(b) - F(a) = \int_a^b f(x) dx\) |
| 二维空间 | (平面上的)连通区域D | (平面上的)有向边界曲线L | 格林公式:$ _L Pdx + Qdy = _D ( - ) d$ |
| 三维空间 | 几何体\(\Omega\) | 外表面\(\Sigma\) | 高斯公式:\(\oiint_\Sigma Pdydz + Qdzdx + Rdxdy = \iiint_\Omega \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right) dv\) |
| 三维空间 | 空间曲面\(\Sigma\) | (空间中的)边界曲线K | 斯托克斯公式: \(\iint_{\Sigma}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right) \mathrm{d} y \mathrm{d} z+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right) \mathrm{d} z \mathrm{d} x+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \mathrm{d} x \mathrm{d} y\)\(=\oint_{\Gamma} P \mathrm{d} x+Q \mathrm{d} y+R \mathrm{d} z\) |
附录2:连通区域
(平面)单连通区域
平面上的单连通区域,简单讲就是内部没有奇点的平面闭区域。
(平面)复连通区域/多连通区域
平面上的多连通区域,简单讲就是平面区域内部存在奇点或者孔洞。
空间二维单连通区域
对空间区域 G,如果G 内任一闭曲面所围成的区域全属于 G,则称 G 是空间二维单连通区域。
空间一维单连通区域
对空间区域 G,如果G 内任一闭曲线总可以张成一片完全属于 G 的曲面,则称 G 为空间一维单连通区域。
eg:环面:环面是空间二维单连通的,但不是空间一维单连通的。 
eg:两个同心球面之间的区域,是空间一维单连通的,但不是空间二维单连通的。