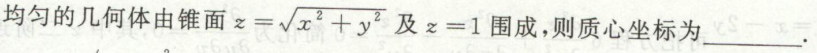高等数学-多元积分学-重积分习题
高等数学-多元积分学-重积分习题
考察重积分的定义与性质
考察重积分的定义
例1
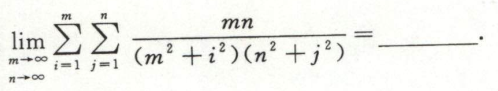

例2


考察重积分的性质
考察积分区域对称性与被积函数奇偶性
例1
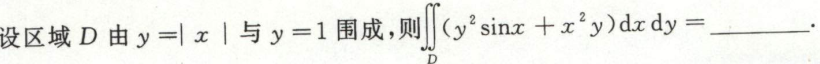
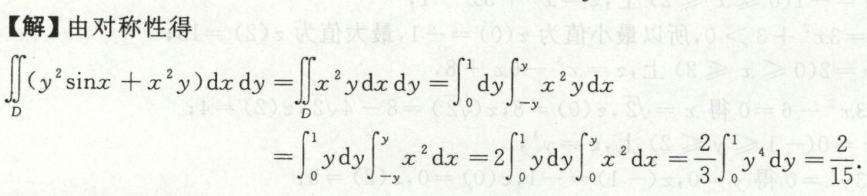
例2 这道题凑了另一半出来,就比较有灵性了
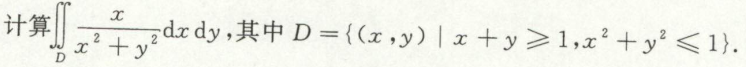
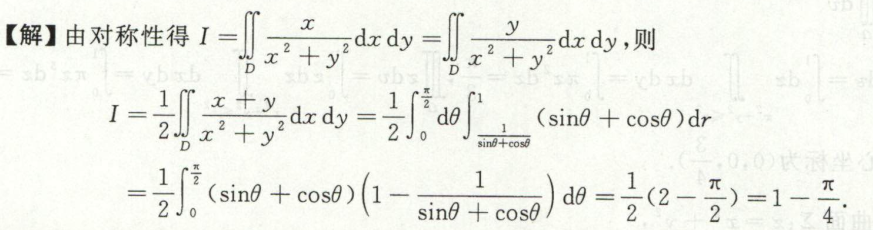
例3 关于y=x对称的一道题
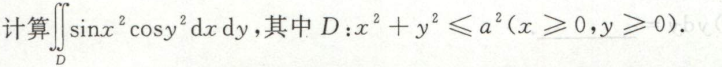

考察二重积分的中值定理
例1
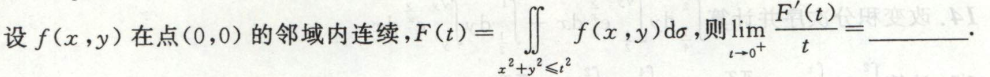
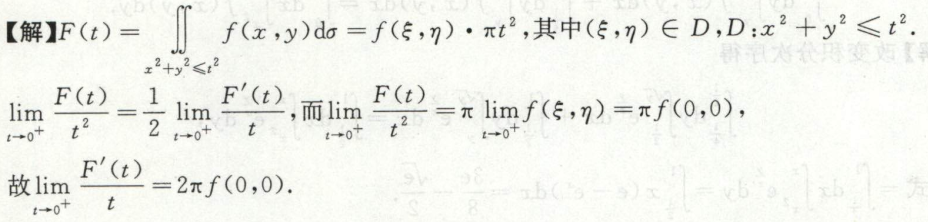
重积分比较大小
例1

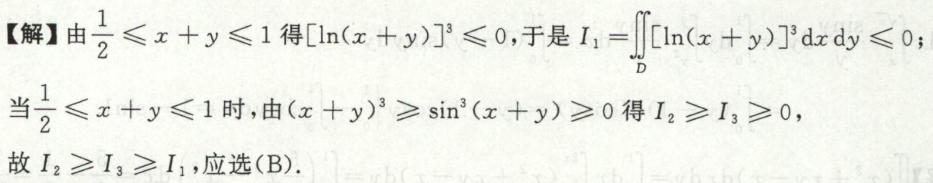
重积分的计算
变换积分次序
不变换积分次序无法计算的情形: \(x^{2 n} e^{\pm x^{2}} d x\) \(e^{\frac{1}{x}} d x\) \(\sin \frac{1}{x} d x\) \(\cos \frac{1}{x} d x\)
例1

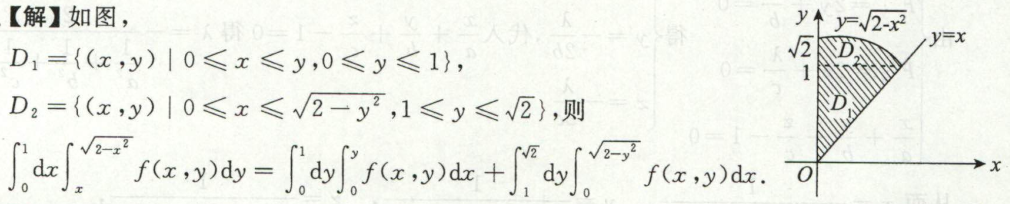
例2


例3
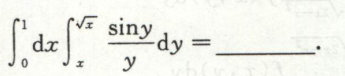
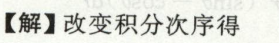

例4

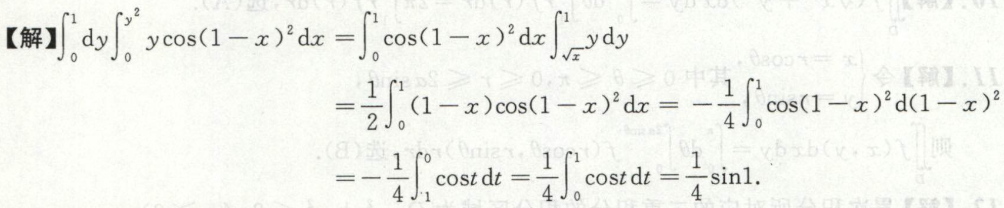
例5
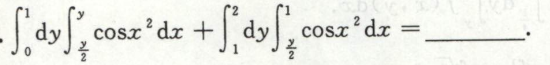

例6
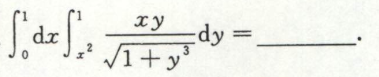
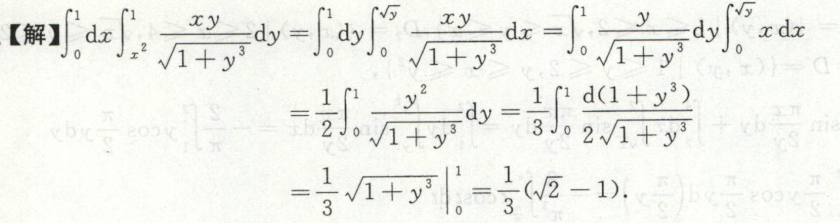
例7

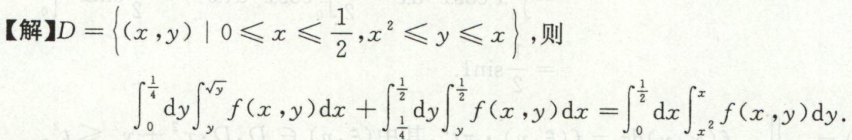
例8
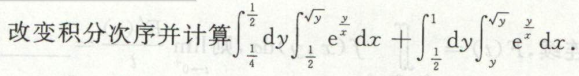
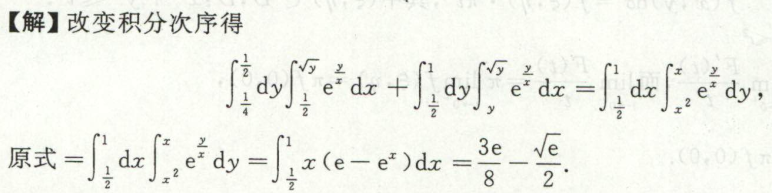
例9
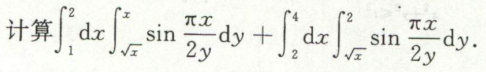

在直角坐标系计算重积分
直接在直角坐标系计算重积分
例1

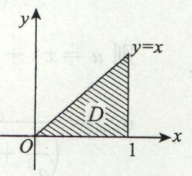
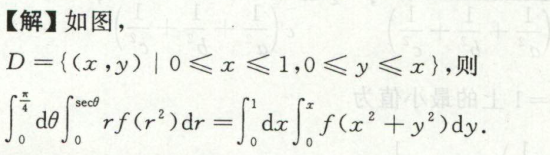
例2
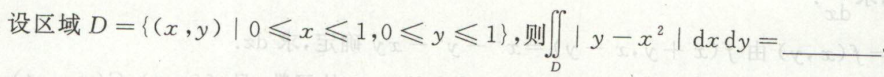
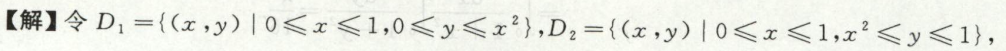
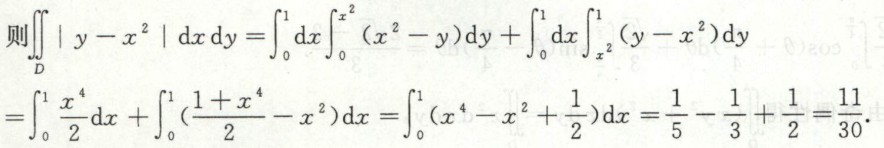
例3


例4
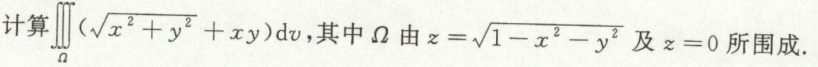

注:此题也可在求坐标系中求解
例5


例6
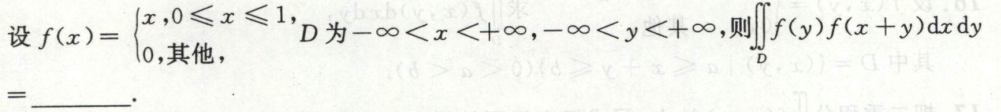

例7


例8

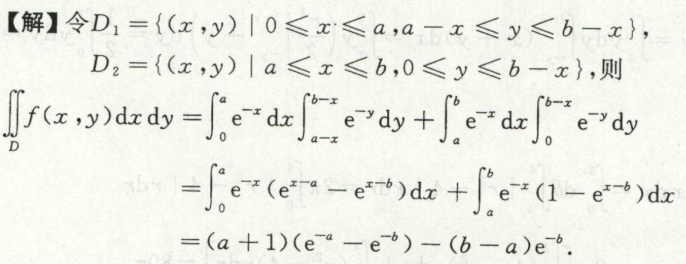
例9


例10
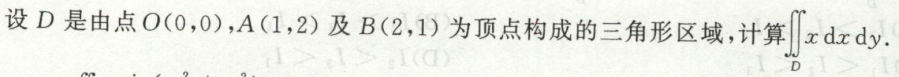

例11
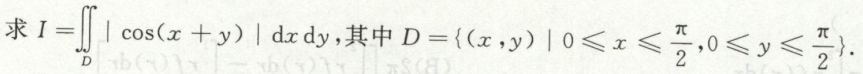

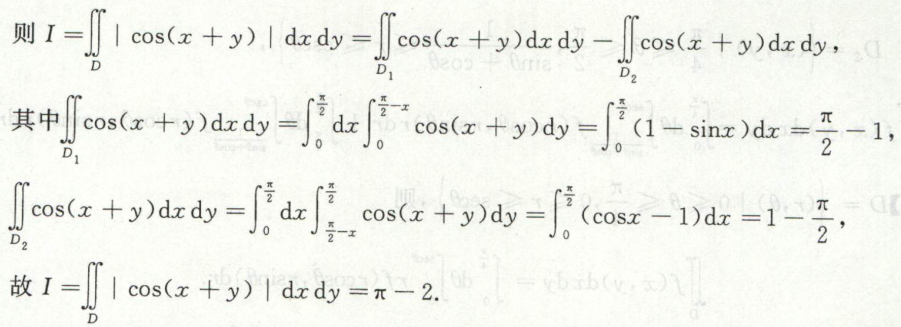
例12


积分区域边界是参数方程形式,计算重积分
例1
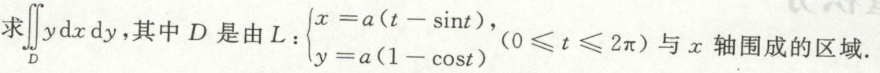
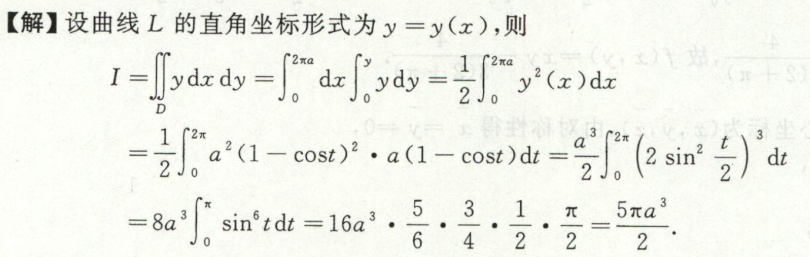
转换到极坐标系计算重积分
某些二重积分,满足: 积分区域D的边界用极坐标方程表示比较简单(主要), 被积函数用极坐标变量\(\rho, \theta\)表示比较简单(次要), 这个时候,我们可以考虑用极坐标来计算二重积分。
例1


例2
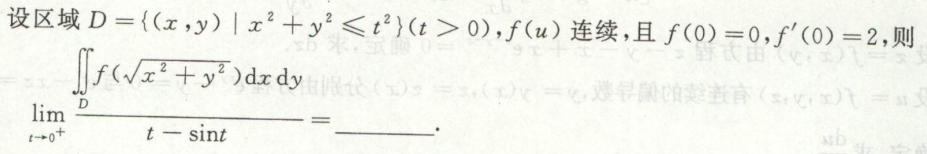

例3
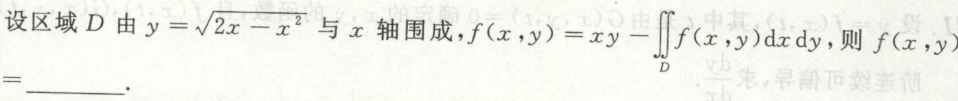
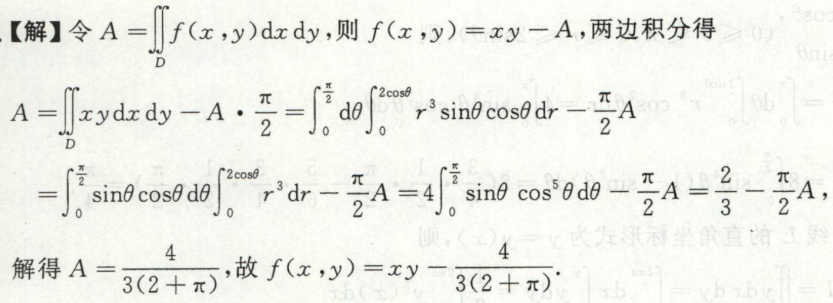
例4
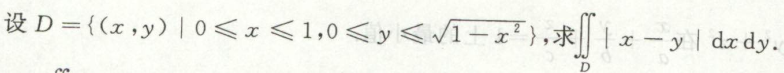

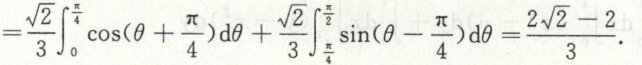
例5
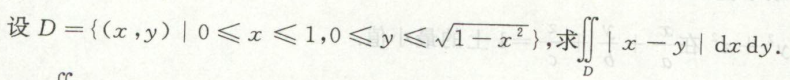

例6


例7


例8

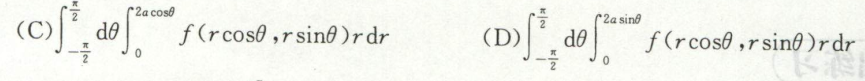

例9



例10

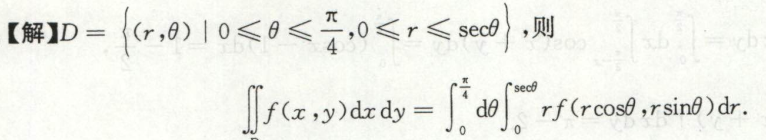
例11


例12
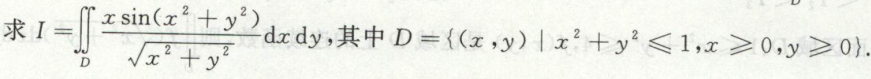
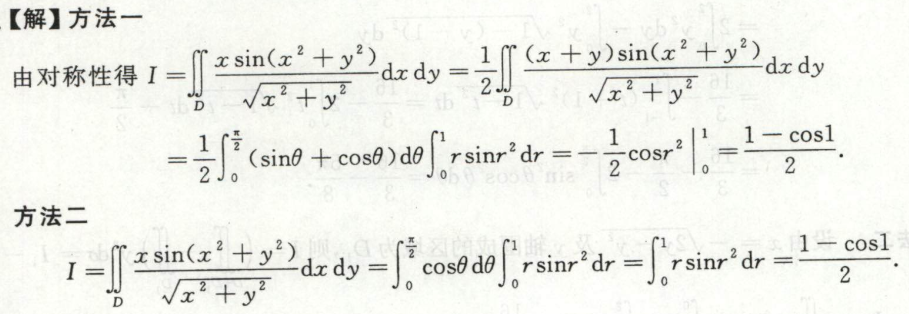
例13


例14 此题比较考验功底

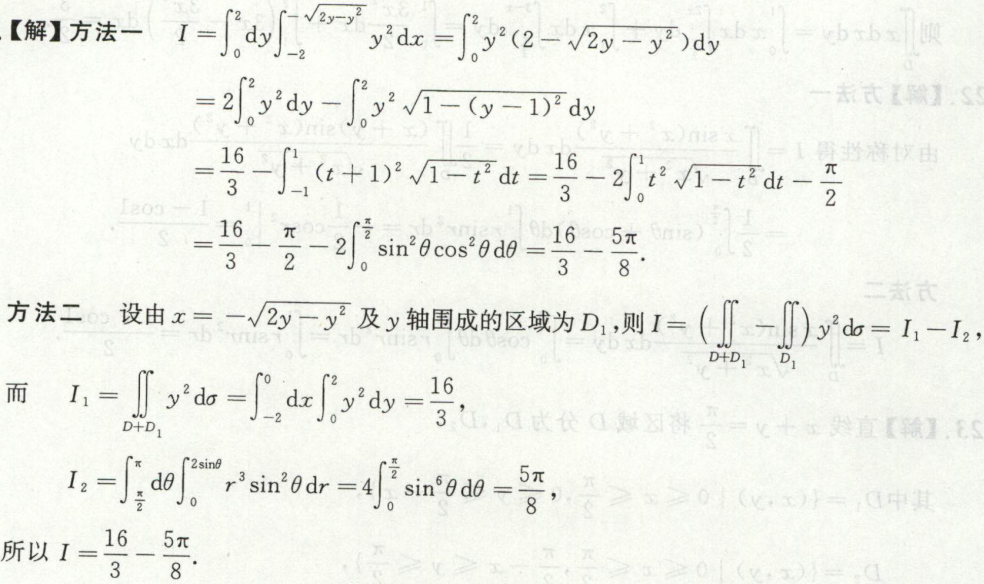
在直角坐标系中求解,注意换元法的使用。 在极坐标系中求解,注意叠加法,可以叠负的(即相减)
例15


例16
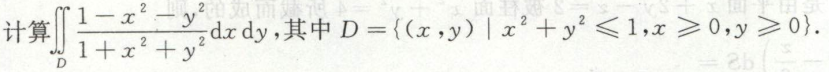

例17


例18


此题转换到球坐标系更简单
转换到柱坐标系求重积分
例1


例2
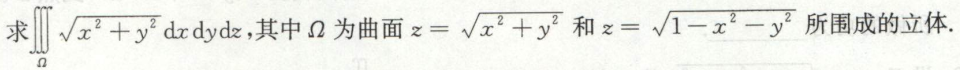

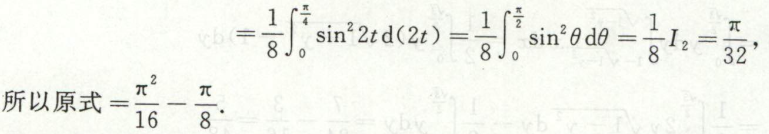
其实此题转换到球坐标系求重积分更简单。
例3

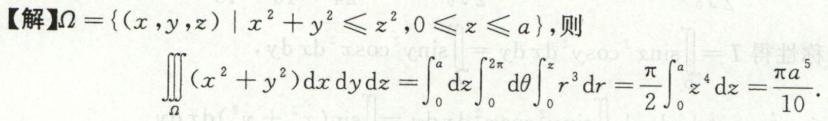
例4


转换到球坐标系中球重积分
例1


例2
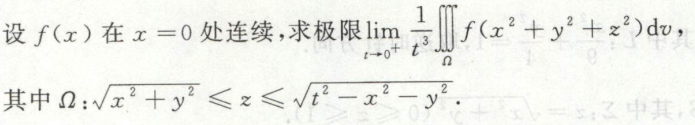

重积分应用
几何应用
体积
例1


物理应用
质心
例1