高等数学-多元积分学-重积分
高等数学-多元积分学-重积分
由一元函数积分学我们知道,定积分是某种形式的和的极限。这种和的极限的概念推广到定义在区域、曲线、曲面上的多元函数的情形,就得到了重积分、曲线积分以及曲面积分的概念。
二重积分的概念与性质
二重积分概念的引入
曲顶柱体的体积
对于平顶柱体体积:体积 = 高 \(\times\) 底面积
对于曲顶柱体,需要将底面(区域)划分为足够小的区域,用极限理论来讨论。
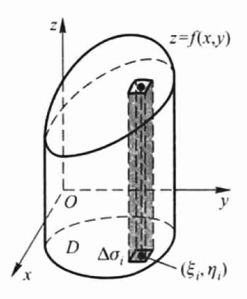
首先,用一组曲线网把 区域D 分成 n 个小闭区域\(\Delta \sigma_{1}, \Delta \sigma_{2}, \cdots, \Delta \sigma_{n}\). 则曲顶柱体可以看作是以小闭区域为底面的小曲顶柱体组成的。
\(f(x, y)\) 连续,对于一个很小的小闭区域\(\Delta \sigma_{i}\)来说 \(, f(x, y)\) 变化很小,我们可以近似看作小平顶柱体。 从\(\Delta \sigma_{i}\)中任取一点\(\left(\xi_{i}, \eta_{i}\right),\) 以 \(f\left(\xi_{i}, \eta_{i}\right)\) 为高而底面积为\(\Delta \sigma_{i}\)的体积为\(f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i} \quad(i=1,2, \cdots, n)\) 则这n个小平顶柱体的总体积为\(\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\),即原曲顶柱体的体积近似为\(\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\)。 当这n个小闭区域的直径的最大值(记作\(\lambda\))趋于0时,取上述和的极限,所得极限自然的定义为曲顶柱面的体积\(V=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\)
注:闭区域的直径指区域上任意两点的最大距离。
平面薄片的质量
对于均匀薄片( 面密度是常数),质量为:质量=面密度 \(\times\) 面积
对于不均匀的薄片,需要将平面(区域)划分为足够小的区域,用极限理论来讨论。
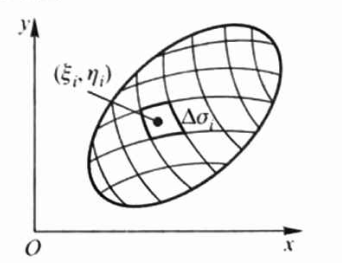
首先,用一组曲线网把 区域D 分成 n 个小闭区域\(\Delta \sigma_{1}, \Delta \sigma_{2}, \cdots, \Delta \sigma_{n}\). 则平面薄板的质量可以看作是以小闭区域(小块)的质量的总和。
由于 \(\mu(x, y)\) 连续,对于每个小块(小 块所占的小闭区域 \(\Delta \sigma_{i}\) 的直径很小),这些小块就可以近似地看做均匀薄片. 在 \(\Delta \sigma_{i}\) 上任取一点 \(\left(\xi_{i}, \eta_{i}\right)\), 以点 \(\left(\xi_{i}, \eta_{i}\right)\)的面密度为近似面密度,这个小块\(\Delta \sigma_{i}\)的近似质量为\(\mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i} \quad(i=1,2, \cdots, n)\)。 对这n个小块的质量求和,即平面薄板的近似总质量为\(\sum_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_i\) 取极限,极限值可自然定义为平面薄板的质量\(m=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\)
二重积分的定义
二重积分的定义
设 \(f(x, y)\) 是有界闭区域 \(D\) 上的有界函数. 将闭区域 D 任意分成 n 个小闭区域\(\Delta \sigma_{1}, \Delta \sigma_{2}, \cdots, \Delta \sigma_{n}\),其中 \(\Delta \sigma_{i}\) 表示第 \(i\) 个小闭区域,也表示它的面积。
在每个 \(\Delta \sigma_{i}\) 上任取一点\(\left(\xi_{i}, \eta_{i}\right),\) 作乘积 \(f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}(i=1,2, \cdots, n),\) 并作和 \(\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\)。
若各小闭区域\(\Delta \sigma_{i}\) 的最大直径\(\lambda \rightarrow 0\)时,和的极限\(\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\)总存在,且极限值且与区域D划分\(\Delta \sigma_{i}\) 的分法无关,也与 \(\Delta \sigma_{i}\) 上\(\left(\xi_{i}, \eta_{i}\right)\)取法无关 , 那么称此极限为函数 \(f(x, y)\) 在闭区域 D 上的二重积分,记作\(\iint_{D} f(x, y) \mathrm{d} \sigma=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\)
其中 \(f(x, y)\) 叫做被积函数 , $ f(x, y) $ 叫做被积表达式 , \(\mathrm{d} \sigma\) 叫做面积元素, ,\(x\) 与 \(y\)叫做积分变量, D 叫做积分区域, \(\sum_{i}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\) 叫做积分和.
二重积分的性质
(二重积分存在的充分条件)当 \(f(x, y)\) 在闭区域 D 上连续时,函数 \(f(x, y)\) 在 \(D\) 上的二重积分必定存在
(数乘和加法性质)设 \(\alpha\) 与 \(\beta\) 为常数,则\(\iint_{D}[\alpha f(x, y)+\beta g(x, y)] \mathrm{d} \sigma=\alpha \iint_{D} f(x, y) \mathrm{d} \sigma+\beta \iint_{D} g(x, y) \mathrm{d} \sigma\)
(积分区域可加性)若\(D\) 分为两个闭区域 \(D_{1}\) 与 \(D_{2}\),则\(\iint_{D} f(x, y) \mathrm{d} \sigma=\iint_{D_{1}} f(x, y) \mathrm{d} \sigma+\iint_{D_{2}} f(x, y) \mathrm{d} \sigma\)
($ f(x, y)=1$时的几何意义)如果在 \(D\)上 ,$ f(x, y)=1\(, 则\)={D} 1 ={D} $ 为 \(D\) 的面积
(二重积分的比较)如果在 \(D\)上$ f(x, y) g(x, y),$ 那么有\(\iint_{D} f(x, y) \mathrm{d} \sigma \leqslant \iint_{D} g(x, y) \mathrm{d} \sigma\)
(重积分的比较的推论)由于\(-|f(x, y)| \leqslant f(x, y) \leqslant|f(x, y)|\),所以有\(\left|\iint_{D} f(x, y) \mathrm{d} \sigma\right| \leqslant \iint_{D}|f(x, y)| \mathrm{d} \sigma\)
(重积分的最值定理/估值不等式)设 \(M\) 和 \(m\) 分别是 \(f(x, y)\) 在闭区域 \(D\) 上的最大值和最小值, \(\sigma\) 是 \(D\)的面积,则有\(m \sigma \leqslant \iint_{D} f(x, y) \mathrm{d} \sigma \leqslant M \sigma\)
(二重积分的中值定理:可用上一条性质证明)设函数 \(f(x, y)\) 在闭区域 \(D\) 上连续, \(\sigma\) 是 \(D\)的面积,则在 D 上至少存在一点( \(\xi, \eta)\), 使得\(\iint_{D} f(x, y) \mathrm{d} \sigma=f(\xi, \eta) \sigma\)
二重积分的积分区域对称性与积分函数奇偶性

积分区域D关于y轴对称(左右对称), 设右侧积分区域为\(D_1\),则(把y先看作常数,观察被积函数对于x的奇偶性) \(\left\{ \begin{aligned}f(-x,y)=-f(x,y), &\Rightarrow \iint_D f(x,y) d\sigma = 0 \\ f(-x,y)= f(x,y), &\Rightarrow \iint_D f(x,y)d\sigma = 2 \iint_{D_1} f(x,y)d\sigma \end{aligned}\right.\)
积分区域D关于x轴对称(上下对称), 设上侧积分区域为\(D_1\),则(把x看作常数,观察被积函数关于y的奇偶性) \(\left\{ \begin{aligned}f(x,-y)=-f(x,y), &\Rightarrow \iint_D f(x,y) d\sigma = 0 \\ f(x,-y)= f(x,y), &\Rightarrow \iint_D f(x,y)d\sigma = 2 \iint_{D_1} f(x,y)d\sigma \end{aligned}\right.\)
积分区域D关于\(y=x\)对称,则: \(\iint_{D} f(x, y) d \sigma=\iint f(y, x) d \sigma\)
二重积分的积分中值定理
若 \(f(x, y)\) 和 \(g(x, y)\) 在 \(D\) 上连续, 且\(g(x, y)\) 在 \(D\) 上不变号, 则存在\((\xi, \eta) \in D,\) 使等式\(\iint_{D} f(x, y) g(x, y) \mathrm{d} \sigma=f(\xi, \eta) \iint_{D} g(x, y) \mathrm{d} \sigma\)成立, 其中 D 是有界连通闭区域.
(用介值定理可以证明,参考:知乎网友的回答)
二重积分的计算
二重积分的计算,除了用定义计算,一般需要化为两次单积分(定积分)来计算。
用定义计算二重积分
略
计算二重积分:在直角坐标系化为二次积分
下面讨论在直角坐标系中将二重积分化为二次定积分的方法。
直角坐标系中的二重积分
根据二重积分的定义\(\iint_{D} f(x, y) \mathrm{d} \sigma=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\),对于闭区域D的划分是任意的。如果在直角坐标系中,用平行于坐标轴的直线网来划分 D,那么除了包含边界点的一些小闭区域外,其余的小闭区域都是矩形闭区域.
设矩形闭区域 \(\Delta \sigma,\) 的边长为 \(\Delta x_{j}\) 和 \(\Delta y_{k},\) 则\(\Delta \sigma_{i}=\Delta x_{j} \cdot \Delta y_{k} \cdot\) 因此在直角坐标系中,有时也把面积元素 \(\mathrm{d} \sigma\) 记作 \(\mathrm{d} x \mathrm{d} y,\)而把(直角坐标系中)二重积分记作\(\iint_{D} f(x, y) \mathrm{d} x \mathrm{d} y\)
其中dxdy 叫做直角坐标系中的面积元素。
X型区域上二重积分的计算
X型二重积分的积分区域如下图所示:

其积分区域D可以用如下不等式来表示:
对于在这种区域上的二重积分,化为先对y积分再对x积分的二次定积分比较简单。(先对y积分时被积函数中出现的x可以当作常数来处理)
\(\iint_{D} f(x, y) \mathrm{d} \sigma=\int_{a}^{b}\left[\int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) \mathrm{d} y\right] \mathrm{d} x = \int_{a}^{b} \mathrm{d} x \int_{\varphi_{1}(x)}^{\varphi_{2}(x)} f(x, y) \mathrm{d} y\)
Y型区域上二重积分的计算
Y型二重积分的积分区域如下图所示:
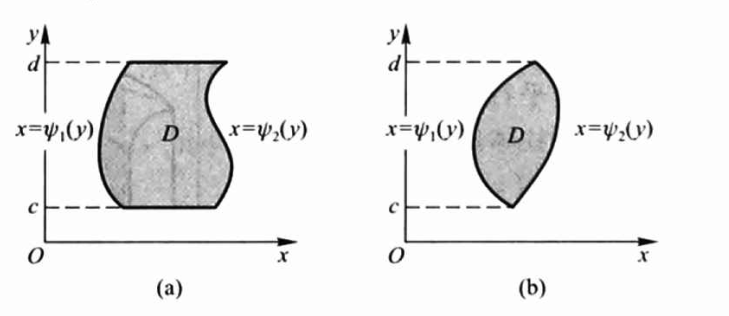
其积分区域D可以用如下不等式来表示: \(\psi_{1}(y) \leqslant x \leqslant \psi_{2}(y), c \leqslant y \leqslant d\)
对于在这种区域上的二重积分,化为先对x积分再对y积分的二次定积分比较简单。(先对x积分时被积函数中出现的y可以当作常数来处理)
\(\iint_{D} f(x, y) \mathrm{d} \sigma=\int_{c}^{d}\left[\int_{\psi_{1}(y)}^{\psi_{2}(y)} f(x, y) \mathrm{d} x\right] \mathrm{d} y = \int_{c}^{d} \mathrm{d} y \int_{\psi_{1}(y)}^{\psi_{2}(y)} f(x, y) \mathrm{d} x\)
混合型区域上二重积分的计算

类似这样的混合型区域上的二重积分,可以拆分成多个X型区域或者Y型区域来计算
计算二重积分:直角坐标系转换为极坐标系,在极坐标系化为二次积分
某些二重积分,满足: 积分区域D的边界用极坐标方程表示比较简单(主要), 被积函数用极坐标变量\(\rho, \theta\)表示比较简单(次要), 这个时候,我们可以考虑用极坐标来计算二重积分。
下面讨论在极坐标
直角坐标系中的二重积分转换为极坐标系中的二重积分
根据二重积分的定义\(\iint_{D} f(x, y) \mathrm{d} \sigma=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\),我们考虑在极坐标系的表示。
二重积分积分区域D的划分是任意的,考虑以极坐标系极轴方向、角向方向划分网格,把积分区域D划分为n个小区域,如下图所示:
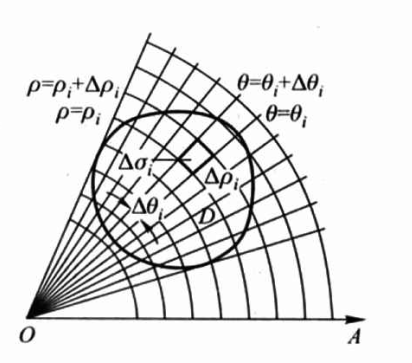
除包含边界点的一些小区域外,小闭区域的\(\Delta \sigma_{i}\)面积可如下表示(扇形面积相减): \(\begin{aligned} \Delta \sigma_{i} &=\frac{1}{2}\left(\rho_{i}+\Delta \rho_{i}\right)^{2} \cdot \Delta \theta_{i}-\frac{1}{2} \rho_{i}^{2} \cdot \Delta \theta_{i}=\frac{1}{2}\left(2 \rho_{i}+\Delta \rho_{i}\right) \Delta \rho_{i} \cdot \Delta \theta_{i} \\ &=\frac{\rho_{i}+\left(\rho_{i}+\Delta \rho_{i}\right)}{2} \cdot \Delta \rho_{i} \cdot \Delta \theta_{i}=\bar{\rho}_{i} \cdot \Delta \rho_{i} \cdot \Delta \theta_{i} \end{aligned}\)
直角坐标与极坐标之间的关系为: \(\left\{\begin{array}{} x = \rho \cos \theta \\ y = \rho \sin \theta\end{array}\right.\) 则小区域\(\Delta \sigma_{i}\)中一点\(\left(\bar{\rho}_{i}, \bar{\theta}_{i}\right)\),直角坐标设为 \(\left(\xi_{i}, \eta_{i}\right)\),则有: \(\left\{\begin{array}{} \xi_{i}=\bar{\rho}_{i} \cos \bar{\theta}_{i} \\ \eta_{i}=\bar{\rho}_{i} \sin \bar{\theta}_{i}\end{array}\right.\)
则根据二重积分定义有:
\(\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\rho_{i} \cos \bar{\theta}_{i}, \bar{\rho}_{i} \sin \bar{\theta}_{i}\right) \bar{\rho}_{i} \cdot \Delta \rho_{i} \cdot \Delta \theta_{i}\)
即极坐标中,二重积分的表示为: \(\iint_{D} f(x, y) \mathrm{d} \sigma=\iint_{D} f(\rho \cos \theta, \rho \sin \theta) \rho \mathrm{d} \rho \mathrm{d} \theta\)
我们也可以得到二重积分的变量从直角坐标到极坐标的 变换公式: \(\iint_{D} f(x, y) \mathrm{d} x \mathrm{d} y=\iint_{D} f(\rho \cos \theta, \rho \sin \theta) \rho \mathrm{d} \rho \mathrm{d} \theta\)
以上也表明,要把二重积分中的变量从直角坐标变换为极坐标,只要 把被积函数中的 x 与 \(y\) 分別换成 \(\rho \cos \theta\) 与 \(\rho \sin \theta .\) 并把直角坐标系 中的面积元素 dxdy 换成极坐标系中的面积元素 \(\rho \mathrm{d} \rho \mathrm{d} \theta\)
极坐标系中二重积分的计算
极坐标系中方便计算的积分区域如下所示: 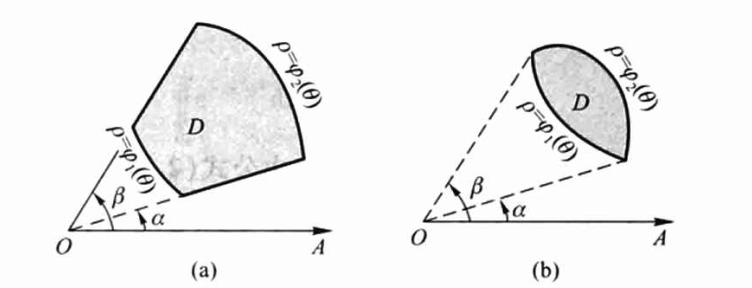
其积分区域D可用如下不等式表示: \(\varphi_{1}(\theta) \leqslant \rho \leqslant \varphi_{2}(\theta), \alpha \leqslant \theta \leqslant \beta\)
\(\iint_{D} f(\rho \cos \theta, \rho \sin \theta) \rho \mathrm{d} \rho \mathrm{d} \theta=\int_{\alpha}^{\beta}\left[\int_{\varphi_{1}(\theta)}^{\varphi_{2}(\theta)} f(\rho \cos \theta, \rho \sin \theta) \rho \mathrm{d} \rho\right] \mathrm{d} \theta\)
\(=\int_{\alpha}^{\beta} \mathrm{d} \theta \int_{\varphi_{1}(\theta)}^{\varphi_{2}(\theta)} f(\rho \cos \theta, \rho \sin \theta) \rho \mathrm{d} \rho\)
对于以下的积分区域,可以看作上面情况的特例:
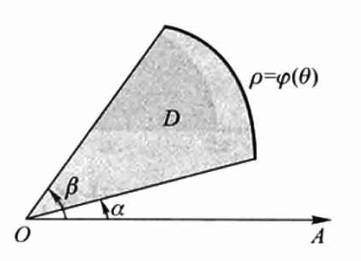
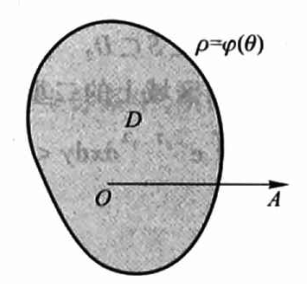
其积分区域D可用如下不等式表示: 特例型1:\(0 \leqslant \rho \leqslant \varphi(\theta), \quad \alpha \leqslant \theta \leqslant \beta\) 特例型2:\(0 \leqslant \rho \leqslant \varphi(\theta), \quad 0 \leqslant \theta \leqslant 2 \pi\)
计算方法不变。
二重积分中坐标系的变换(换元)
定理:设 \(f(x, y)\) 在 \(x O y\) 平面上的闭区域 D 上连续, 若变换\(T: x=x(u, v), y=y(u, v)\)将 uOv 平面上的闭区域 D’变为 xOy 平面上的 D, 且满足: (1)$x(u, v), y(u, v) $在 \(D^{\prime}\)上具有一阶连续偏导数 (2)在 D’上雅可比式\(J(u, v)=\frac{\partial(x, y)}{\partial(u, v)} \neq 0\) (3)变换 \(T: D^{\prime} \rightarrow D\) 是一对一的 , 则有\(\iint_{D} f(x, y) \mathrm{d} x \mathrm{d} y=\iint_{D^{\prime}} f[x(u, v), y(u, v)]|J(u, v)| \mathrm{d} u \mathrm{d} v\),称为二重积分的换元公式。
(证明见 高等数学 同济 第七版(下))
注:雅可比行列式\(J(u,v) = \left|\begin{array}{ll}x_{u}(u, v) & x_{v}(u, v) \\ y_{u}(u, v) & y_{v}(u, v)\end{array}\right|\) 上面的定理中出现的是雅可比行列式的绝对值\(|J(u,v)|\)
二重积分改变积分次序
二重积分选定合适的坐标系、变换为二次积分,就可以计算求解了。
如果变换积分次序,二次积分更好计算(或者不变换积分次序无法计算),可以考虑变换积分次序。
根据积分区域及其边界,可以对二次积分变换积分次序
不变换积分次序无法计算的情形: \(x^{2 n} e^{\pm x^{2}} d x\) \(e^{\frac{1}{x}} d x\) \(\sin \frac{1}{x} d x\) \(\cos \frac{1}{x} d x\)
三重积分的概念与性质
定积分和二重积分作为和的极限的概念,可以很容易推广到三重积分。
三重积分的定义
设 \(f(x, y, z)\) 是空间有界闭区域 \(\Omega\) 上的有界函数. 将 \(\Omega\) 任 意分成 \(n\) 个小比区域\(\Delta v_{1}, \Delta v_{2}, \cdots, \Delta v_{n}\),其中 \(\Delta v_{i}\) 表示第 \(i\) 个小闭区域,也表示它的体积. 在每个 \(\Delta v_{i}\) 上任取一点\(\left(\xi_{i}, \eta_{i}, \zeta_{i}\right),\) 作乘积 \(f\left(\xi_{i}, \eta_{i}, \zeta_{i}\right) \Delta v_{i} \quad(i=1,2, \cdots, n),\)并作和 \(\sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}, \zeta_{i}\right) \Delta v_{i}\), 如果各小闭区域直径中的最大值 \(\lambda \rightarrow 0\) 时,这和的极限总存在,且与闭区域$ $的分法及点 \(\left(\xi_{i}, \eta_{i}, \zeta_{i}\right)\) 的取法无关,那么称此极限为函数 \(f(x, y, z)\) 在闭区域 \(\Omega\) 上的三重积分,记作\(\iiint_{\Omega} f(x, y, z) \mathrm{d} v=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} f\left(\xi_{i}, \eta_{i}, \zeta_{i}\right) \Delta v_{i}\)
其中 \(f(x, y, z)\) 叫做被积函数, \(\mathrm{d} v\) 叫做体积元素, \(\Omega\) 叫做积分区域.
直角坐标系中的三重积分
在直角坐标系中,如果用平行于坐标面的平面来划分 \(\Omega\),那么除了包含 \(\Omega\) 的边界点的一些不规则小闭区域外,得到的小闭区域$ v_{i}$ 为长方体。 设长方体小闭区域 \(\Delta v_{i}\) 的边长为 \(\Delta x_{j}, \Delta y_{k}\) 与 \(\Delta z_{l},\) 则 \(\Delta v_{i}=\Delta x_{j} \Delta y_{k} \Delta z_{l} .\) 因 此 在直角坐标系中,有 时也扑体积元素 \(d v\) 记作 \(\mathrm{d} x \mathrm{d} y \mathrm{d} z,\) 而把三重积分记作\(\iiint_{\Omega} f(x, y, z) \mathrm{d} x \mathrm{d} y \mathrm{d} z\)
三重积分的性质
三重积分的而行之与二重积分的性质一致。
这里特别注意一下三重积分奇偶性对称性。
三重积分的积分区域的对称性和被积函数的奇偶性
被积区域\(\Omega\)关于\(xOy\)面对称(上下对称),设上侧区域为\(\Omega_1\), \(\left\{ \begin{aligned}f(x,y,-z)=-f(x,y,z), &\Rightarrow \iint_\Omega f(x,y,z) dv = 0 \\ f(x,y,-z)= f(x,y,z), &\Rightarrow \iint_\Omega f(x,y,z)dv = 2 \iint_{\Omega_1} f(x,y,z)dv \end{aligned}\right.\)
被积区域\(\Omega\)关于\(yOz\)面对称(前后对称),设前侧区域为\(\Omega_1\), \(\left\{ \begin{aligned}f(-x,y,z)=-f(x,y,z), &\Rightarrow \iint_\Omega f(x,y,z) dv = 0 \\ f(-x,y,z)= f(x,y,z), &\Rightarrow \iint_\Omega f(x,y,z)dv = 2 \iint_{\Omega_1} f(x,y,z)dv \end{aligned}\right.\)
被积区域\(\Omega\)关于\(zOx\)面对称(左右对称),设前侧区域为\(\Omega_1\), \(\left\{ \begin{aligned}f(x,-y,z)=-f(x,y,z), &\Rightarrow \iint_\Omega f(x,y,z) dv = 0 \\ f(x,-y,z)= f(x,y,z), &\Rightarrow \iint_\Omega f(x,y,z)dv = 2 \iint_{\Omega_1} f(x,y,z)dv \end{aligned}\right.\)
三重积分的中值定理
类似二重积分的中值定理,容易推广到三重积分
三重积分的计算
计算三重积分:在直角坐标系化为三次积分
在直角坐标系中将三重积分化为三次定积分有两种思路:投影法和截平面法
投影法计算三重积分
将空间区域\(\Omega\)投影到平面闭区域上,如投影到\(xOy\)平面(或者\(yOz\)平面、\(xOz\)平面),对应的投影平面记为\(D_{xy}\)。
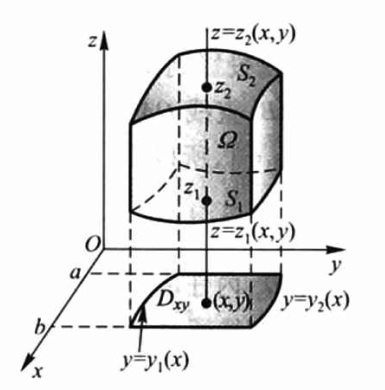
这种情况下,积分区域可表示为: \(\Omega=\left\{(x, y, z) \mid z_{1}(x, y) \leqslant z \leqslant z_{2}(x, y),(x, y) \in D_{x y}\right\}\)
先将\(f(x,y,z)\)看作z的函数(x,y先当作常数),先计算在z轴的积分,然后计算在投影区域上的二重积分,即: \(\iint_{\Omega} f(x, y, z) \mathrm{d} v=\iint_{D_{y}}\left[\int_{z_{1}(x, y)}^{z_{2}\left(x_{y}, y\right)} f(x, y, z) \mathrm{d} z\right] \mathrm{d} \sigma\)
其中二重积分也可以写成二次积分,最终化为三次积分: \(\iiint_{\Omega} f(x, y, z) \mathrm{d} v=\int_{a}^{b} \mathrm{d} x \int_{y_{1}(x)}^{y_{2}(x)} \mathrm{d} y \int_{z_{1}(x, y)}^{z_{2}(x, y)} f(x, y, z) \mathrm{d} z\)
截平面法计算三重积分
如果(以竖坐标为例)在竖坐标为z的位置,以平面将积分区域\(\Omega\)截开,则可以根据积分区域边界条件写出截面区域\(D_z\)。
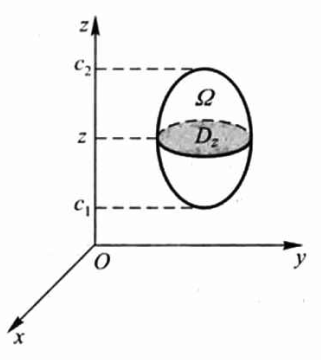
空间区域可以表示为: \(\Omega=\left\{(x, y, z) \mid(x, y) \in D_{z}, c_{1} \leqslant z \leqslant c_{2}\right\}\)
我们可以先把z看作定值,计算在截面区域\(D_z\)上的二重积分,然后z轴积分,即: \(\iiint_{\Omega} f(x, y, z) \mathrm{d} v=\int_{c_{1}}^{c_{2}} \mathrm{d} z \iint_{D} f(x, y, z) \mathrm{d} x \mathrm{d} y\)
其中二重积分也可以写成二次积分,最终化为三次积分。
计算三重积分:直角坐标系转换为柱坐标系,在柱坐标系化为三次积分
直角坐标系与柱坐标系的转换
在柱坐标系中,按极向、角向、竖轴向,将积分区域\(\Omega\)划分为许多小闭区域除,了含$ $的边界点 的一些不规则小闭区域外, 这种小闭区域都是柱体.

考虑由 \(\rho, \theta\) 和 \(z\) 各取得微小增量 $d , d$和 $dz $所成的柱体的体积。这个体积等于高与底面 积的乘积. 现在高为 dz、底面积在不计高阶无穷小时为 \(\rho \mathrm{d} \rho \mathrm{d} \theta\) (即极坐标系中的面积元素),于是得柱坐标系的体积元素\(\mathrm{d} v=\rho \mathrm{d} \rho \mathrm{d} \theta \mathrm{d} z\)
点在直角坐标系和柱坐标系的坐标关系为: \(\left\{\begin{array}{l}x=\rho \cos \theta \\ y=\rho \sin \theta \\ z=z\end{array}\right.\)
直角坐标系中的三重积分化为柱坐标系中的三重积分为:
\(\iiint_{\Omega} f(x, y, z) \mathrm{d} x \mathrm{d} y \mathrm{d} z=\iiint_{\Omega} F(\rho \cos \theta, \rho \sin \theta, z) \rho \mathrm{d} \rho \mathrm{d} \theta \mathrm{d} z=\iiint_{\Omega} F(\rho, \theta, z) \rho \mathrm{d} \rho \mathrm{d} \theta \mathrm{d} z\)
其中\(F(\rho, \theta, z)=f(\rho \cos \theta, \rho \sin \theta, z)\)
柱坐标系中投影法或截面法化为三次积分
然后类比直角坐标系中的方法,用投影法或截面法(可能按柱面截取)将三重积分化为三次积分。
计算三重积分:直角坐标系转换为球坐标系,在球坐标系化为三次积分
直角坐标系与球坐标系的转换

点的坐标在直角坐标系和球坐标系的关系为: \(\left\{\begin{array}{l}x=O P \cos \theta=r \sin \varphi \cos \theta \\ y=O P \sin \theta=r \sin \varphi \sin \theta \\ z=r \cos \varphi\end{array}\right.\)
按球坐标系径向和两个角向,将积分区域\(\Omega\)化为许多小闭区域,把积分区域 \(\Omega\) 分成许多小闭区域.

考虑由 r, $$ 和 \(\theta\)各取得微小增量 $dr, d$和 $d$所成的六面体的体积。 不计高阶无穷小,可把这个六面体看做长方体,其经线方向的长为 \(rd\varphi\),纬线方向的宽为\(r \sin\varphi d\theta\), 向径方向的高为 dr, 于是得球坐标系的体积元素\(\mathrm{d} v=r^{2} \sin \varphi \mathrm{d} r \mathrm{d} \varphi \mathrm{d} \theta\)
于是得到三重积分变量从直角坐标系转换到球坐标系的公式: \(\iiint_{\Omega} f(x, y, z) \mathrm{d} x \mathrm{d} y \mathrm{d} z=\iiint_{\Omega} F(r, \varphi, \theta) r^{2} \sin \varphi \mathrm{d} r \mathrm{d} \varphi \mathrm{d} \theta\)
球坐标系中投影法或截面法化为三次积分
然后类比直角坐标系中的方法,用投影法或截面法(可能按球面截取)将三重积分化为三次积分。
二重积分、三重积分的计算流程
综上,可以归纳二重积分、三重积分的计算流程: 1)作图,明确积分区域与边界。判断用哪种坐标比较简单 2)注意奇偶性,对称性 3)在对应的坐标系中,化为多次积分
重积分的应用
主要是定积分中元素法的推广。
应用过程中,如果变换坐标系,可以使积分区域的表达式更简单,被积函数更简单,可以考虑变换坐标系。
几何应用
| 曲顶柱体的体积 | 二重积分 | |
|---|---|---|
| 曲面面积的计算 | 二重积分 | 投影的到\(xOy\)面计算:(也可投影到其他面) \(A=\iint_{D} \sqrt{1+f_{x}^{2}(x, y)+f_{y}^{2}(x, y)} \mathrm{d} \sigma = \iint_{D} \sqrt{1+\left(\frac{\partial z}{\partial x}\right)^{2}+\left(\frac{\partial z}{\partial y}\right)^{2}} \mathrm{d} x \mathrm{d} y\) |
曲面面积的计算
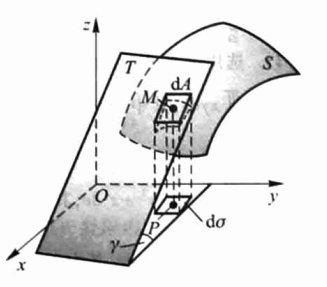
设区域D是被积曲面在\(xOy\)面的投影。将投影区域D划分成许多小闭区域\(d \sigma\),每个小闭区域对应曲面上的一小块,而这一小块的面积近似于从小块上找个切平面对应的面积\(dA\)。
根据几何,有如下关系: \(\mathrm{d} A=\frac{\mathrm{d} \sigma}{\cos \gamma}\) 又有: \(\cos \gamma=\frac{1}{\sqrt{1+f_{x}^{2}(x, y)+f_{y}^{2}(x, y)}}\)
由此可以得到曲面的面积元素: \(\mathrm{d} A=\sqrt{1+f_{x}^{2}(x, y)+f_{y}^{2}(x, y)} \mathrm{d} \sigma\)
从而曲面的面积为:(曲面投影到\(xOy\)面作为积分区域计算) \(A=\iint_{D} \sqrt{1+f_{x}^{2}(x, y)+f_{y}^{2}(x, y)} \mathrm{d} \sigma = \iint_{D} \sqrt{1+\left(\frac{\partial z}{\partial x}\right)^{2}+\left(\frac{\partial z}{\partial y}\right)^{2}} \mathrm{d} x \mathrm{d} y\)
类似的,也可以投影到\(yOz\)平面计算曲面面积: \(A=\iint_{D_{y z}} \sqrt{1+\left(\frac{\partial x}{\partial y}\right)^{2}+\left(\frac{\partial x}{\partial z}\right)^{2}} \mathrm{d} y \mathrm{d} z\) 同样,也可以投影到\(xOz\)平面计算曲面面积: \(A=\iint_{D_{\mathrm{ax}}} \sqrt{1+\left(\frac{\partial y}{\partial z}\right)^{2}+\left(\frac{\partial y}{\partial x}\right)^{2}} \mathrm{d} z \mathrm{d} x\)
物理应用
| 平面薄片的质量 | 二重积分 | \(\iint_{D} \mu(x, y) \mathrm{d} \sigma=\lim _{\lambda \rightarrow 0} \sum_{i=1}^{n} \mu\left(\xi_{i}, \eta_{i}\right) \Delta \sigma_{i}\) |
|---|---|---|
| 空间物体的质量 | 三重积分 | \(\iint_{\Omega} f(x, y, z) \mathrm{d} v\) |
| 平面薄片的质心 | 二重积分 | \(\bar{x}=\frac{M_{,}}{M}=\frac{\iint_{D} x \mu(x, y) \mathrm{d} \sigma}{\iint_{D} \mu(x, y) \mathrm{d} \sigma}, \quad y=\frac{M_{x}}{M}=\frac{\iint_{D} y \mu(x, y) \mathrm{d} \sigma}{\iint_{D} \mu(x, y) \mathrm{d} \sigma}\) |
| 空间物体的质心 | 三重积分 | \(\bar{x}=\frac{\iint_{\Omega} x \mu(x, y, z) \mathrm{d} v}{\iint_{\Omega} \mu(x, y, z) \mathrm{d} v}, \quad \bar{y}=\frac{\iint_{\Omega} y \mu(x, y, z) \mathrm{d} v}{\iint_{\Omega} \mu(x, y, z) \mathrm{d} v}, \quad \bar{z}=\frac{\iint_{\Omega} y \mu(x, y, z) \mathrm{d} v}{\iint_{\Omega} \mu(x, y, z) \mathrm{d} v}\) |
| 平面薄片的转动惯量 | 二重积分 | 在\(xOy\)面上的一个平面薄板, 对x轴,对y轴的转动惯量为\(I_{x}=\sum_{i=1}^{n} y_{i}^{2} m_{i}, \quad I_{y}=\sum_{i=1}^{n} x_{i}^{2} m_{i}\), 对z轴的转动惯量为\(I_z=\sum_{i=1}^{n} (x_{i}^{2} + y_{i}^{2}) m_{i} = I_x + I_y\) |
| 空间物体的转动惯量 | 三重积分 | 空间物体的转动惯量(以z轴为转轴): \(I_{z}=\iiint_{\Omega}r_{i}^{2} m_i \mathrm{d} m=\iiint_{\Omega}\left(x^{2}+y^{2}\right) \mu(x,y,z) \mathrm{d} v\) |
| 空间物体对质点的引力 | 三重积分 | 考虑一个体积为\(\Omega\)的物体,对\((x_0,y_0,z_0)\)处单位质点的引力为:\(\boldsymbol{F} =\left(\boldsymbol{F}_{x}, \boldsymbol{F}_{y}, \boldsymbol{F}_{z}\right) \\ =\left(\iiint_{\Omega} \frac{\boldsymbol{G} \boldsymbol{\rho}(x, y, z)\left(x-x_{0}\right)}{r^{3}} \mathrm{d} v, \iint_{\Omega} \frac{G \boldsymbol{\rho}(x, y, z)\left(y-y_{0}\right)}{r^{3}} \mathrm{d} v,\iiint_{\Omega} \frac{G \rho(x, y, z)\left(z-z_{0}\right)}{r^{3}} \mathrm{d} v\right)\) |
质心
由力学知道,质点系的质心坐标为:
\(\bar{x}=\frac{M_{y}}{M}=\frac{\sum_{i=1} m_{i} x_{i}}{\sum_{i=1}^{n} m_{i}}, \quad \bar{y}=\frac{M_{x}}{M}=\frac{\sum_{i=1} m_{i} y_{i}}{\sum_{i=1}^{n} m_{i}}\)
由质心的定义,我们可以计算如下:
平面薄片的质心: \(\bar{x}=\frac{M_{,}}{M}=\frac{\iint_{D} x \mu(x, y) \mathrm{d} \sigma}{\iint_{D} \mu(x, y) \mathrm{d} \sigma}, \quad \bar{y}=\frac{M_{x}}{M}=\frac{\iint_{D} y \mu(x, y) \mathrm{d} \sigma}{\iint_{D} \mu(x, y) \mathrm{d} \sigma}\)
空间物体的质心: \(\bar{x}=\frac{\iint_{\Omega} x \mu(x, y, z) \mathrm{d} v}{\iint_{\Omega} \mu(x, y, z) \mathrm{d} v}, \quad \bar{y}=\frac{\iint_{\Omega} y \mu(x, y, z) \mathrm{d} v}{\iint_{\Omega} \mu(x, y, z) \mathrm{d} v}, \quad \bar{z}=\frac{\iint_{\Omega} z \mu(x, y, z) \mathrm{d} v}{\iint_{\Omega} \mu(x, y, z) \mathrm{d} v}\)
转动惯量
由力学知道,质点系对于某轴的转动惯量为\(I=\sum_{i=1}^{n} r_{i}^{2} m_{i}\),其中\(r_i\)是各质点到此轴的距离。
平面薄板的转动惯量: 在\(xOy\)面上的一个平面薄板, 对x轴,对y轴的转动惯量为\(I_{x}=\sum_{i=1}^{n} y_{i}^{2} m_{i}, \quad I_{y}=\sum_{i=1}^{n} x_{i}^{2} m_{i}\), 对z轴的转动惯量为\(I_z=\sum_{i=1}^{n} (x_{i}^{2} + y_{i}^{2}) m_{i} = I_x + I_y\)
空间物体的转动惯量(以z轴为转轴): \(I_{z}=\iiint_{\Omega}r_{i}^{2} m_i \mathrm{d} m=\iiint_{\Omega}\left(x^{2}+y^{2}\right) \mu(x,y,z) \mathrm{d} v\)
引力
两质点间引力大小为\(F= \frac{G m_1 m_2}{r^2}\) , 包括方向的矢量式为\(\overrightarrow{F}= \frac{G m_1 m_2 \overrightarrow{r}}{r^3}=\frac{G m_1 m_2 \overrightarrow{e_r}}{r^2}=\frac{G m_1 m_2 }{r^2} \cdot (\cos \alpha, \cos \beta, \cos \gamma)=(F_x, F_y, F_z)\)
考虑一个体积为\(\Omega\)的物体,对\((x_0,y_0,z_0)\)处单位质点的引力为:\(\begin{aligned} \boldsymbol{F} &=\left(\boldsymbol{F}_{x}, \boldsymbol{F}_{y}, \boldsymbol{F}_{z}\right) \\ &=\left(\iiint_{\Omega} \frac{\boldsymbol{G} \boldsymbol{\rho}(x, y, z)\left(x-x_{0}\right)}{r^{3}} \mathrm{d} v, \iint_{\Omega} \frac{G \boldsymbol{\rho}(x, y, z)\left(y-y_{0}\right)}{r^{3}} \mathrm{d} v,\iiint_{\Omega} \frac{G \rho(x, y, z)\left(z-z_{0}\right)}{r^{3}} \mathrm{d} v\right)\end{aligned}\)
含参变量的积分
含参变量积分的定义
设 \(f(x, y) \text { 是矩形 ( 闭区域 }) R=[a, b] \times[c, d]\) 血上的连续函数。(这是一个矩形区间,又称直区间)
\(\varphi(x)=\int_{c}^{d} f(x, y) \mathrm{d} y \quad(a \leqslant x \leqslant b)\)
这个积分的值依赖于取定的 x 值. 当 x 的值改变时,一般说来这个积分的值也跟着改变. 这个积分确定一个定义在[ a,b]上的 x 的函数,x在计算积分的过程中当作常数,通常称作参变量,\(\varphi (x)\)称作含参变量的积分。
含参变量积分的性质
定理 1 (含参变量积分函数的连续性1) 如果函数 \(f(x, y)\) 在矩形 \(R=[a, b] \times[c, d]\) 上连续, 那么由积分\(\int_{c}^{d} f(x, y) \mathrm{d} y\)确定的函数 \(\varphi(x)\) 在 \([a, b]\) 上也连续.
(用闭区间连续必一致连续,用以计算\(\Delta \varphi\)也趋于0,即连续。详细证明见 高等数学 同济第七版(下))
定理 2 (连续函数在直区间的积分次序可交换性) 如果函数 \(f(x, y)\) 在矩形 \(R=[a, b] \times[c, d]\) 上连续, 那么\(\int_{a}^{b}\left[\int_{c}^{d} f(x, y) \mathrm{d} y\right] \mathrm{d} x=\int_{c}^{d}\left[\int_{a}^{b} f(x, y) \mathrm{d} x\right] \mathrm{d} y\) 也可写成\(\int_{a}^{b} \mathrm{d} x \int_{c}^{d} f(x, y) \mathrm{d} y=\int_{c}^{d} \mathrm{d} y \int_{a}^{b} f(x, y) \mathrm{d} x\)
(即函数在直区间连续,则积分次序可交换,这是重积分的性质)
定理 3 (含参变量函数的可微性1) 如果函数 \(f(x, y)\) 及其偏导数 \(f_{x}(x, y)\) 都在矩形 \(R=[a, b] \times[c, d]\) 上连续, 那么由积分\(\int_{c}^{d} f(x, y) \mathrm{d} y\)确定的函数 \(\varphi(x) \text { 在[ } a, b]\) 上可微分, 并且\(\varphi^{\prime}(x)=\frac{\mathrm{d}}{\mathrm{d} x} \int_{c}^{d} f(x, y) \mathrm{d} y=\int_{c}^{d} f_{x}(x, y) \mathrm{d} y\)
(用导数的定义、一致连续性、拉格朗日中值定理证明。详细证明见 高等数学 同济第七版(下))
定理 4 (含参变量积分函数的连续性2) 如果函数 \(f(x, y)\) 在矩形 \(R=[a, b] \times[c, d]\) 上连续, 函数 \(\alpha(x)\) 与 \(\beta(x)\) 在区间 \([a, b]\) 上连续 \(,\) 且\(c \leqslant \alpha(x) \leqslant d, c \leqslant \beta(x) \leqslant d \quad(a \leqslant x \leqslant b)\), 那么由\(\Phi(x)=\int_{\alpha(x)}^{\beta(x)} f(x, y) \mathrm{d} y\)确定的函数\(\Phi(x)\)也连续。
(拆项用定义证,详细证明见 高等数学 同济第七版(下))
定理 5 (含参变量函数的可微性2) 如果函数 \(f(x, y)\) 及其偏导数 \(f_{x}(x, y)\) 都在矩形 \(R=[a, b] \times[c, d]\)上连续, 函数 \(\alpha(x)\) 与 \(\beta(x)\) 都在区间 \([a, b]\) 上可微, 且\(c \leqslant \alpha(x) \leqslant d, c \leqslant \beta(x) \leqslant d \quad(a \leqslant x \leqslant b)\), 那么由\(\Phi(x)=\int_{\alpha(x)}^{\beta(x)} f(x, y) \mathrm{d} y\)确定的函数\(\Phi(x)\)也在 \([a, b]\) 上可微 \(,\) 且函数的微分为:(莱布尼兹公式) \(\begin{aligned} \Phi^{\prime}(x) &=\frac{\mathrm{d}}{\mathrm{d} x} \int_{\alpha(x)}^{\beta(x)} f(x, y) \mathrm{d} y \\ &=\int_{\alpha(x)}^{\beta(x)} f_{x}(x, y) \mathrm{d} y+f[x, \beta(x)] \beta^{\prime}(x)-f[x, \alpha(x)] \alpha^{\prime}(x) \end{aligned}\)
(拆项用定义证,详细证明见 高等数学 同济第七版(下))