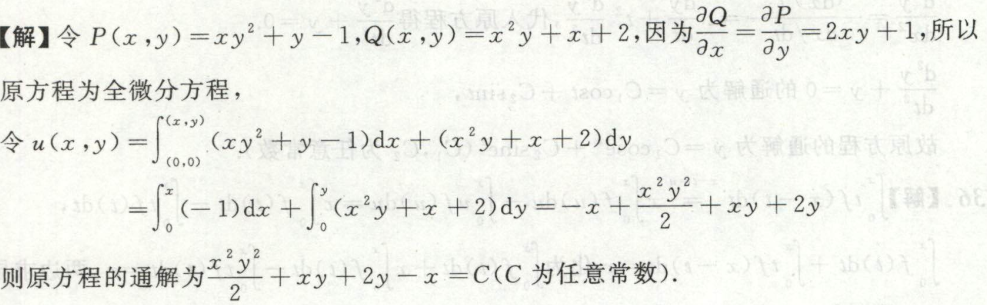高等数学-微分方程习题
高等数学-微分方程习题
解一阶微分方程
解可分离变量微分方程
例1

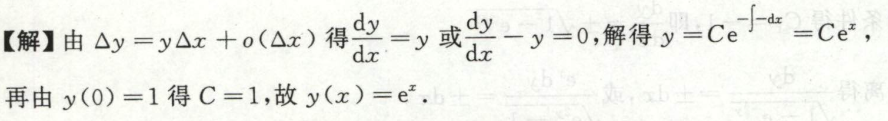
例2

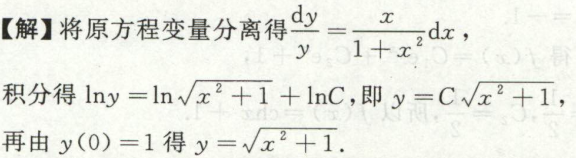
例3
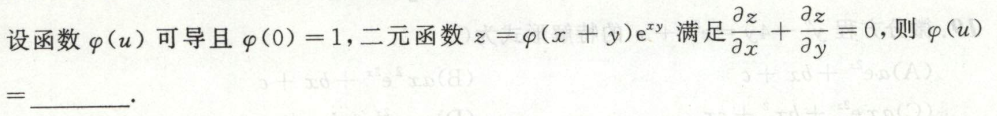
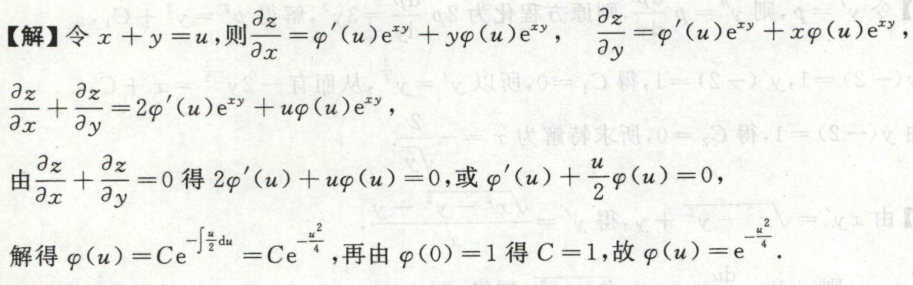
例4
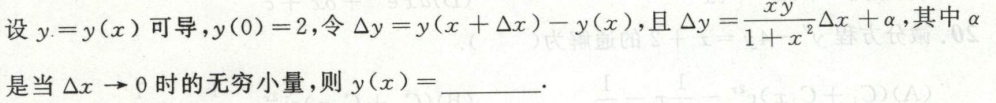
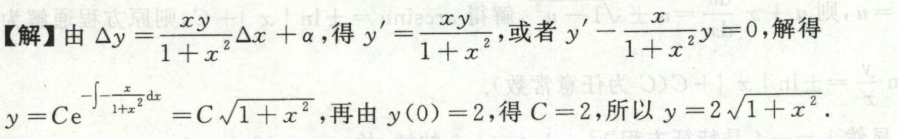
例5
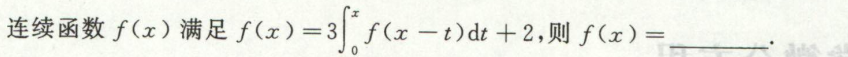
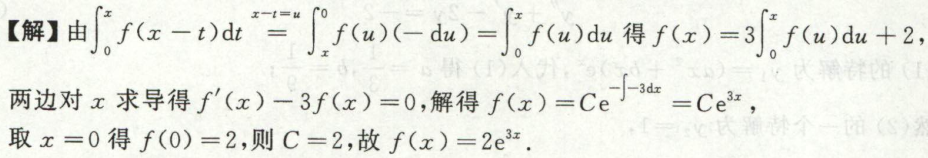
例6


例7
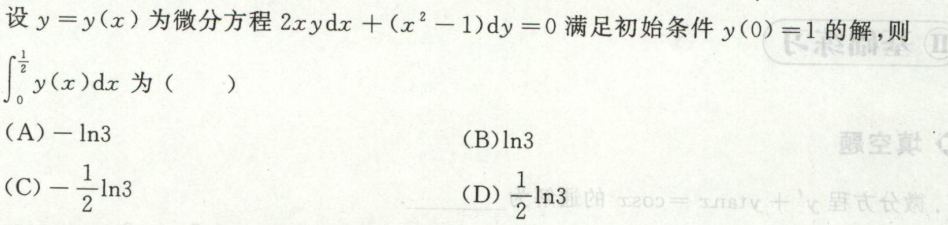
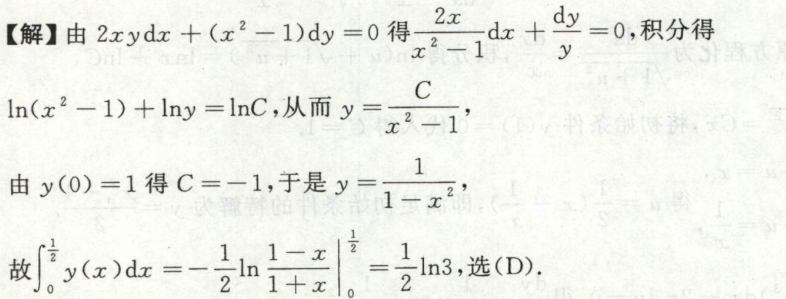
例8
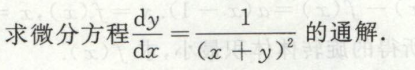


例9


例10

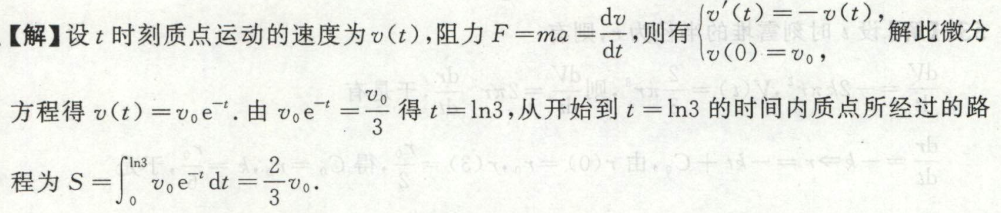
例11


解齐次方程
齐次方程,这里指一阶[y与x齐次]微分方程
例1


例2
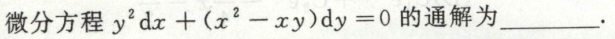

例3
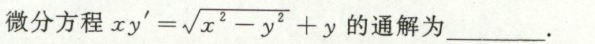
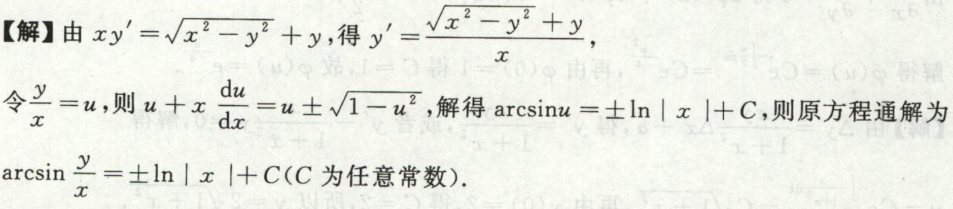
例4


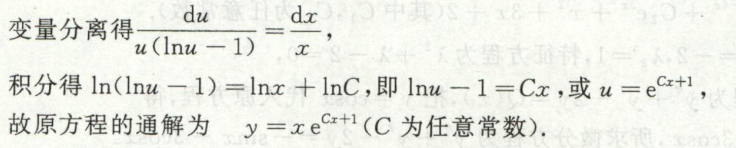
例5
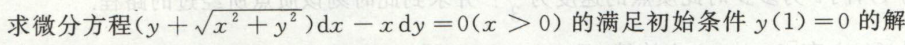

例6
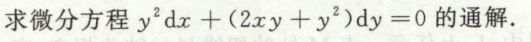

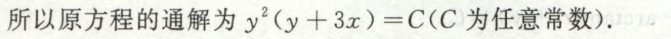
例7


例8

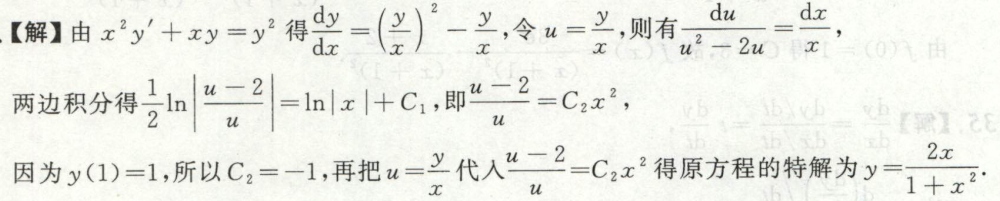
例9


解可降为一阶的微分方程
解可降阶的\(y^{\prime \prime}=f\left(y, y^{\prime}\right)\)型微分方程
例1

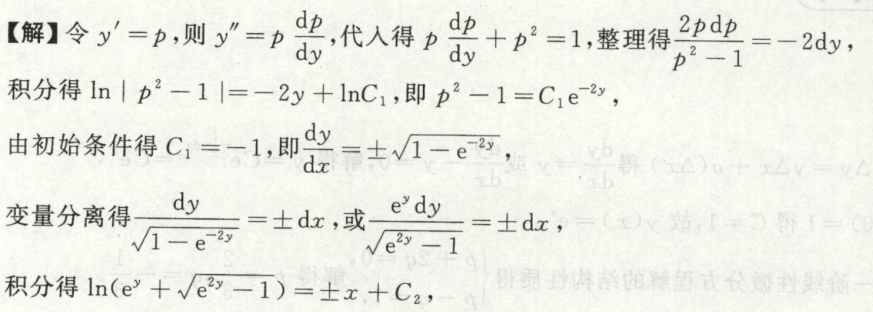
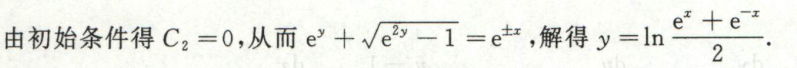
例2
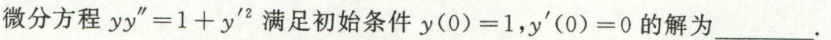

例3
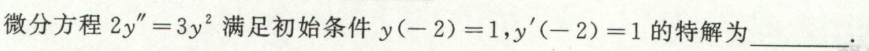
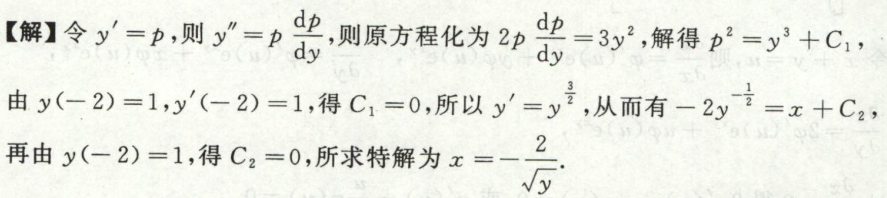
例4


例5 注意技巧

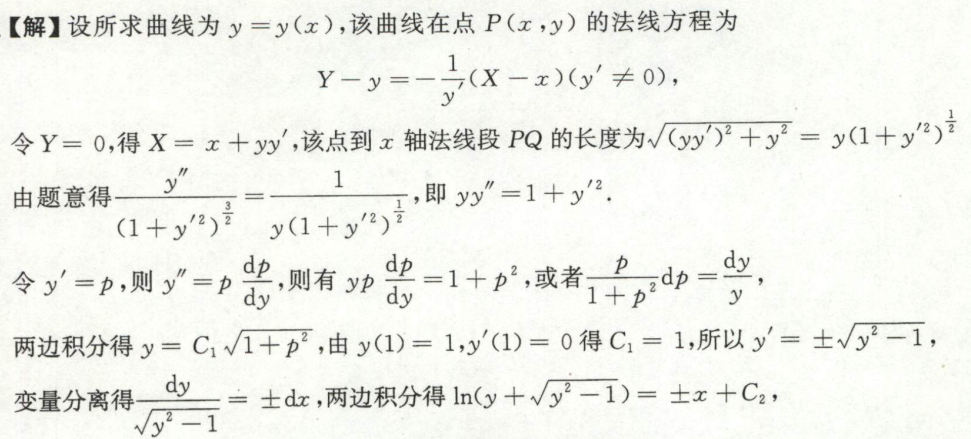
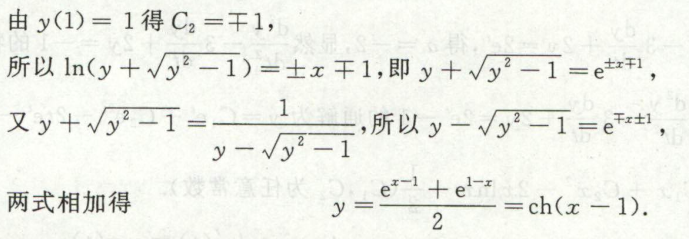
解可降阶的\(y^{\prime \prime}=f\left(x, y^{\prime}\right)\)型微分方程
例1


例2
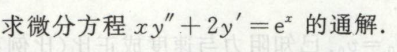
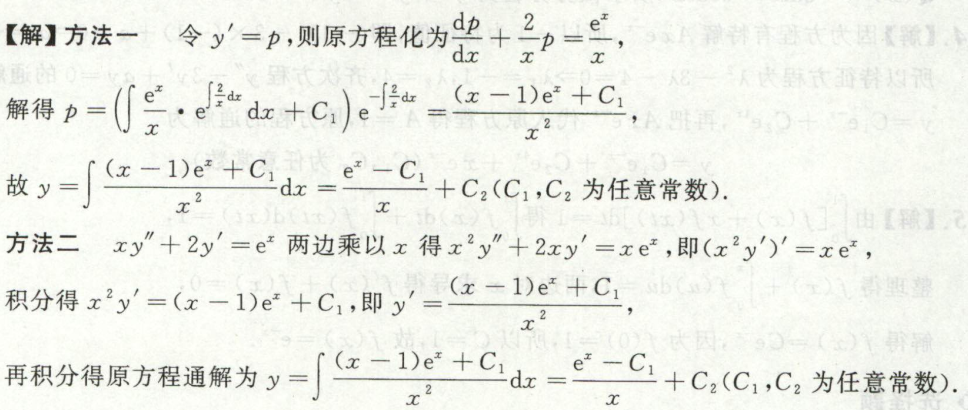
例3

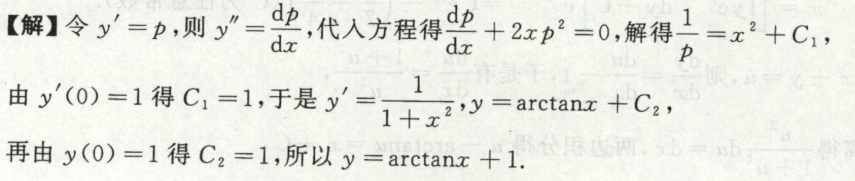
线性微分方程
线性微分方程解的结构与性质
例1


我是将解代入左边做的
例2
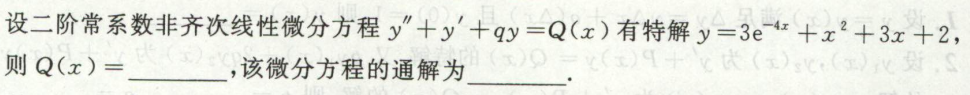
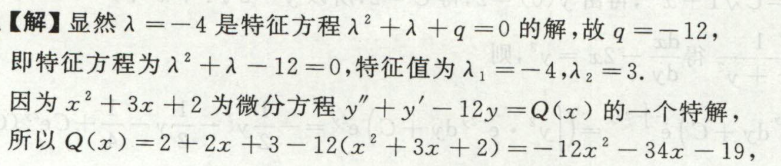

例3
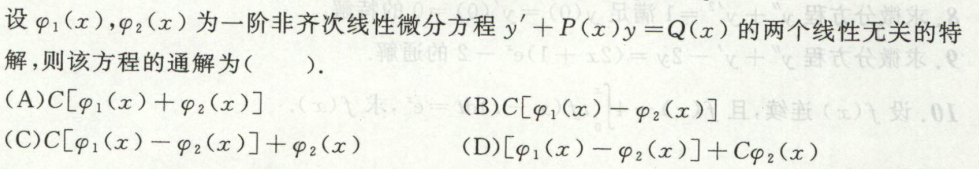
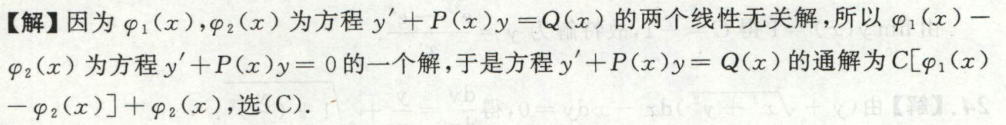
解一阶线性微分方程
解一阶齐次线性微分方程:公式法/分离变数法
可以看作可分离变量的一阶微分方程来求解
也可以直接套一阶线性微分方程的公式
习题详见解可分离变量微分方程
解一阶非齐次线性微分方程:公式法/(分离变量法+常数变易法)
先用分离变量法求对应的一阶齐次线性微分方程的通解,再用分离变量法求非齐次线性方程的解。
或者直接套公式\(y=\mathrm{e}^{-\int P(x) \mathrm{d} x}\left(\int Q(x) \mathrm{e}^{\int P(x) \mathrm{d} x} \mathrm{d} x+C\right)\)
例1
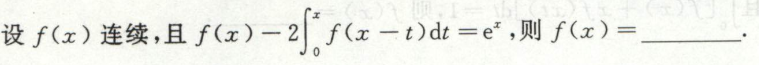

例2


例3
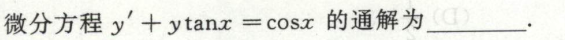

例4
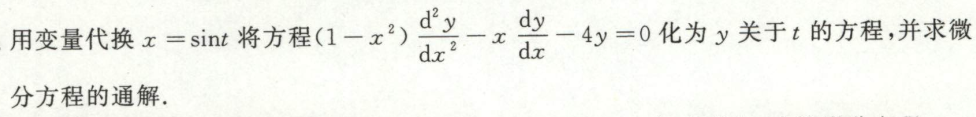
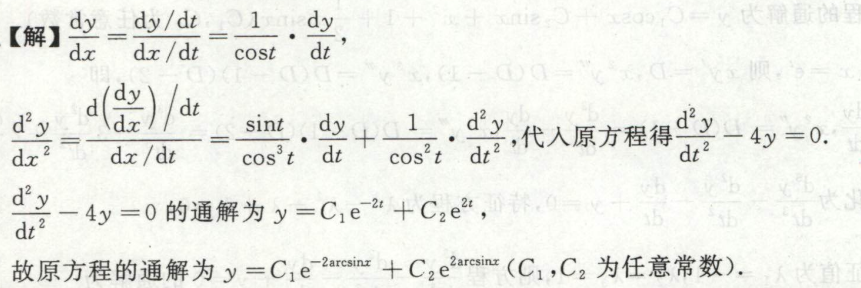
例5


例6 未完成:没有积出来


例7

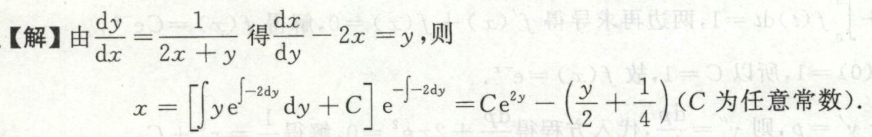
例8 变量代换的灵活使用


这道题把\(\cos y \frac{dy}{dx}\)看作\(\frac{d(\sin y)}{dx}\)使用\(u=siny\)的 代换,后面又使用了\(z=\frac{1}{u}\)代换,最后才变成可分离变量的微分方程。
例9
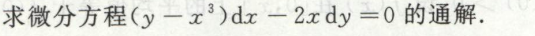

这里是用一阶线性微分方程的公式法来解的。如果用常数变易法,就会发现x只能取\(x>0\)
例10
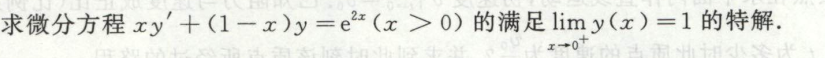

例11



这里将x看作自变量,y看作因变量,就可以解了
例12
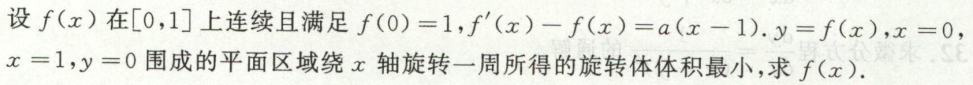
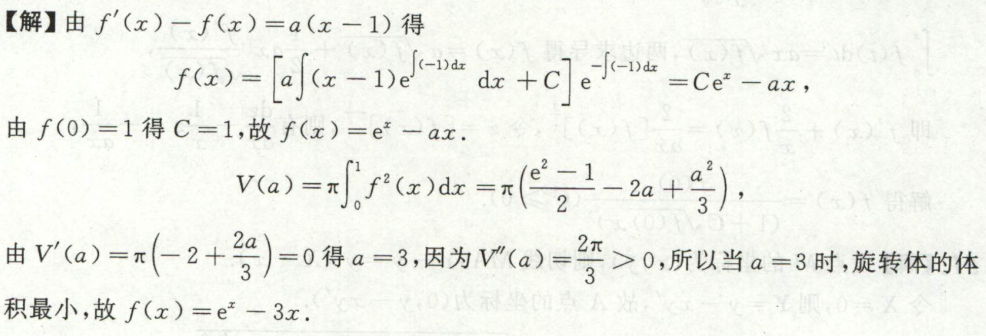
解常系数线性微分方程
解常系数齐次线性微分方程:特征方程法
例1
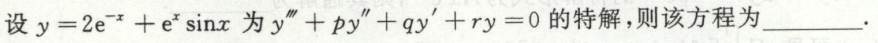

这里,给了常系数齐次线性微分方程的特解,对应通解的形式为\(y= C_1 e^{r_1 x} + e^{\alpha x} (C_2 \cos \beta x + C_3 \sin \beta x)\),从而可以确定对应的特征方程的特征值,继而确定特征方程,最后确定常系数齐次线性微分方程的系数。
例2
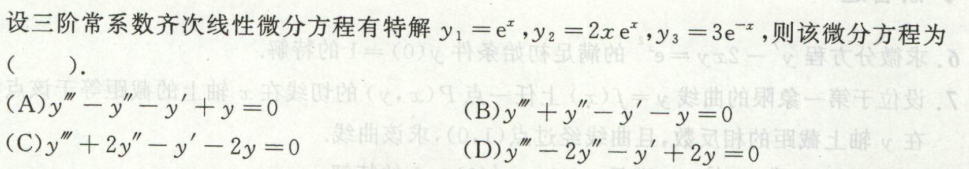

例3

例4


解常系数非齐次线性微分方程:特征方程法+待定系数法
解常系数非齐次线性微分方程,需要先用特征方程法求出对应的齐次方程通解,再用待定系数法求出非齐次方程特解,最终得到非齐次线性方程通解
例1
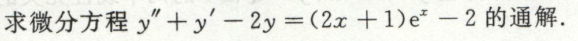
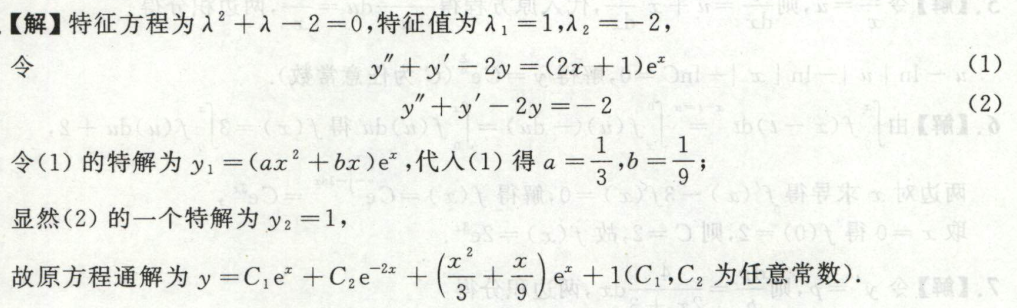
例2


例3

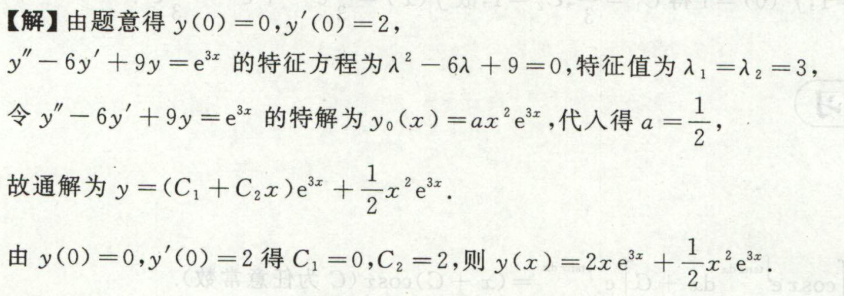
例4


例5

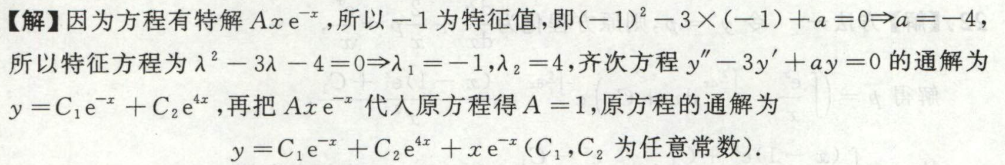
例5


例6


例7



例8


例9


例10
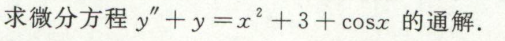

非线性方程
解伯努利方程
例1

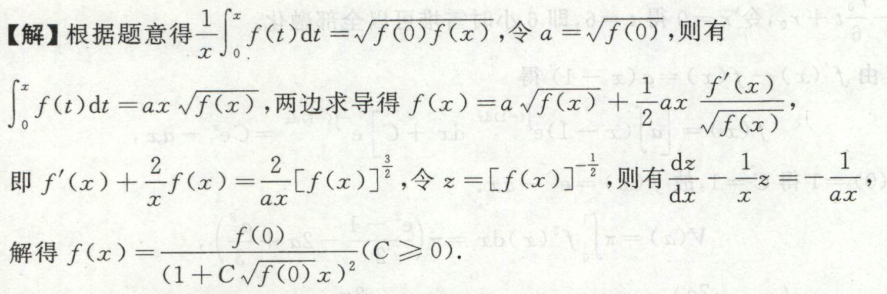
解欧拉方程
例1

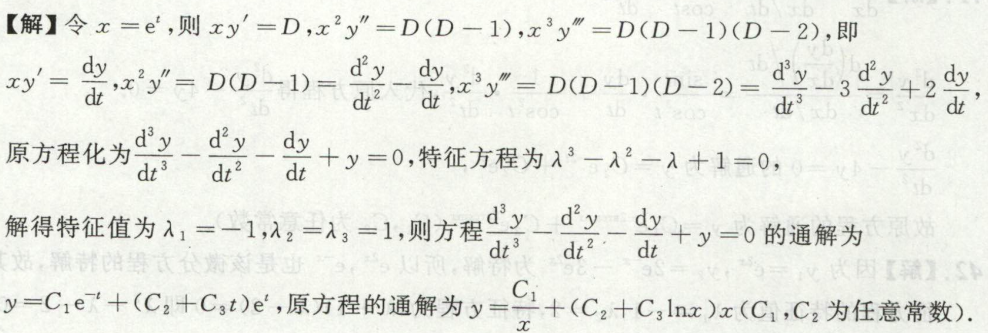
例2


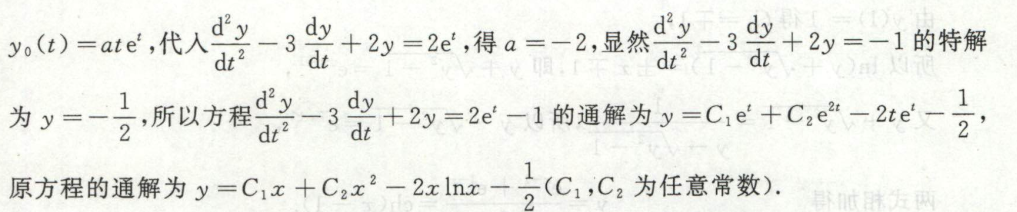
全微分方程
例1