高等数学-级数习题
高等数学-级数习题
级数审敛
级数收敛定义与性质判敛
例1
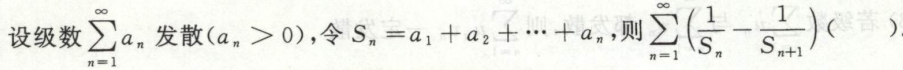



例2


例3


例4

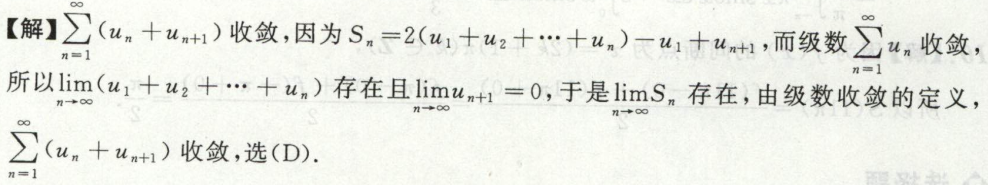
例5




例6


例7


正项级数审敛
比较审敛与极限审敛
比较审敛法的一般形式,以及基本不等式的应用
例1
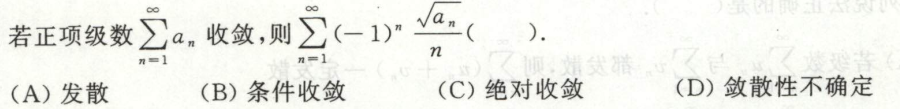

(主要是根据不等式:\(a+b \ge 2\sqrt{ab}\))
例2


(A选项主要根据基本不等式:\(\left(\frac{a + b}{2}\right)^2 \le \frac{a^2+b^2}{2}\)以及\(\left(\frac{a - b}{2}\right)^2 \le \frac{a^2+b^2}{2}\))
例3


例4


例5

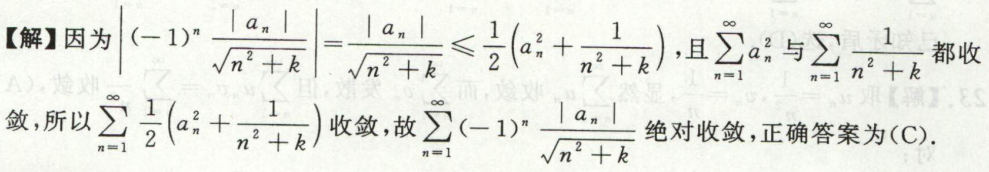
(此题也可以用比值审敛法做)
例6
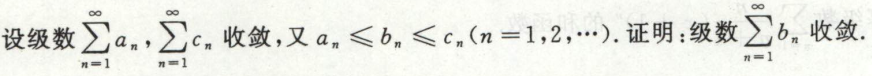

例7
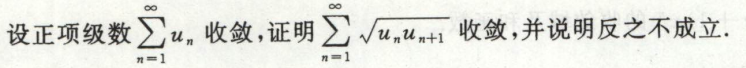

例8

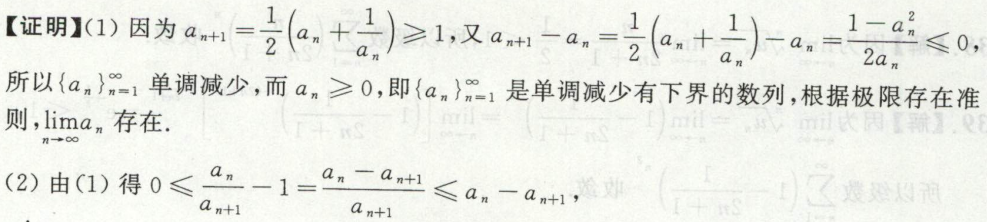

例9

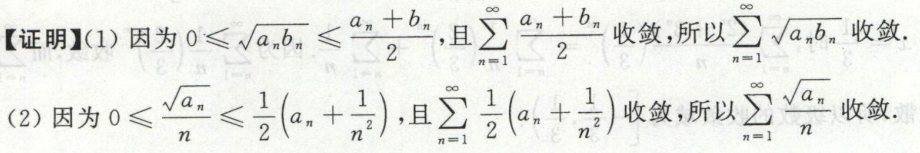
例10


极限审敛法/比较审敛法的极限形式,以及等价/同阶/高阶无穷小的应用
例1

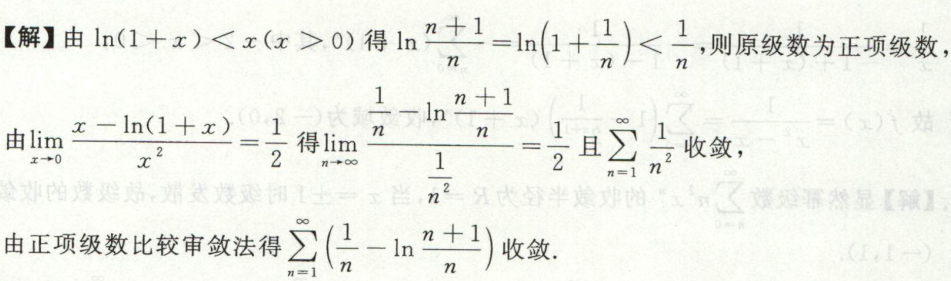
例2


例3
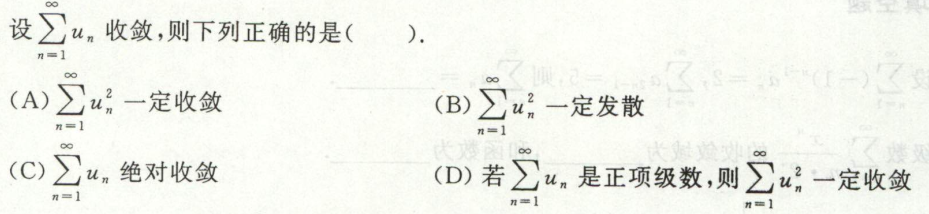

例4

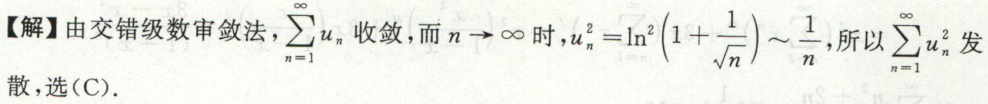
例5


例6



例7


例8
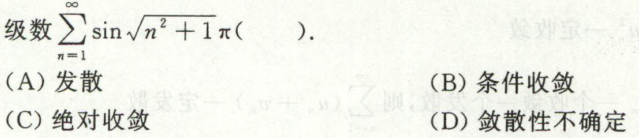

例9


例10


例11

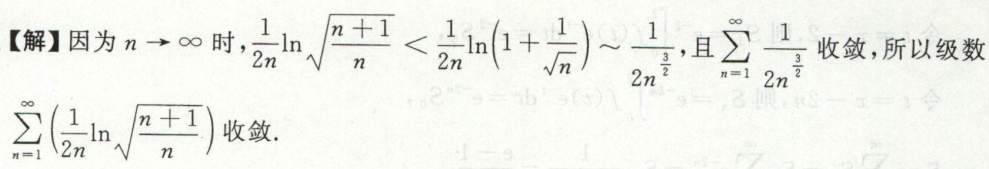
例12 此题需要功底


例13 此题需要功底


比值审敛法
例1
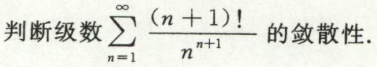
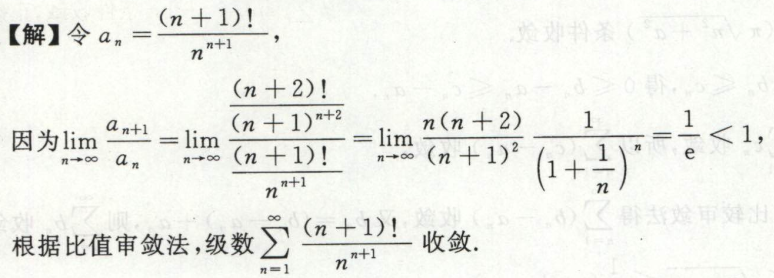
例2
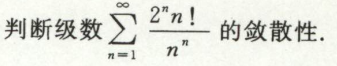

根值审敛法
例1

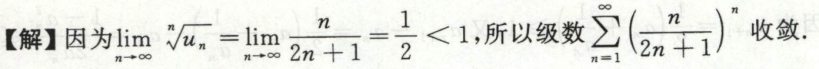
例2
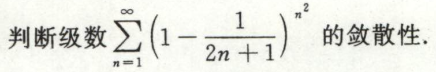
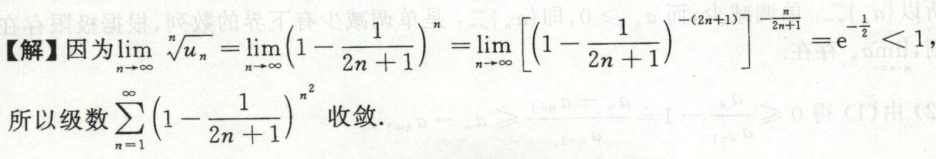
交错级数审敛
例1


例2


例3
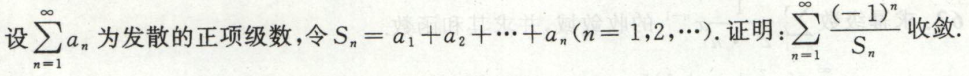

例4


求级数收敛范围
求p级数收敛范围
例1


求幂级数的收敛域
例1


例2
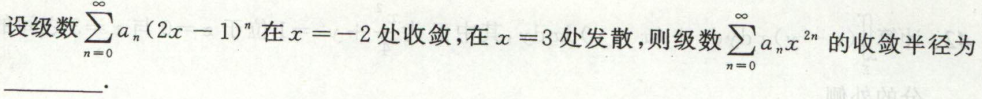

例3

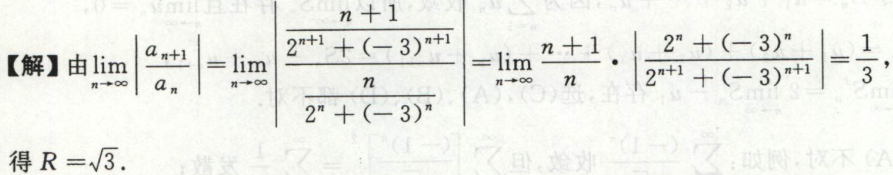
例4
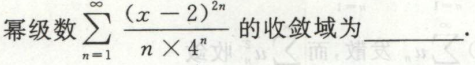

例5
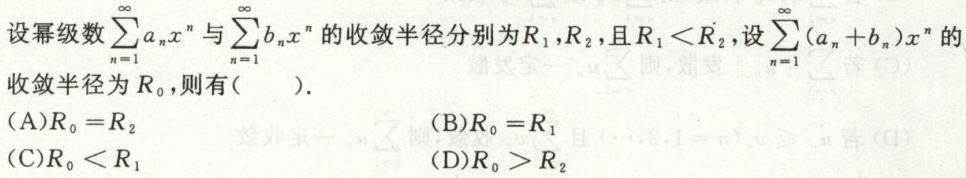

例6


例7

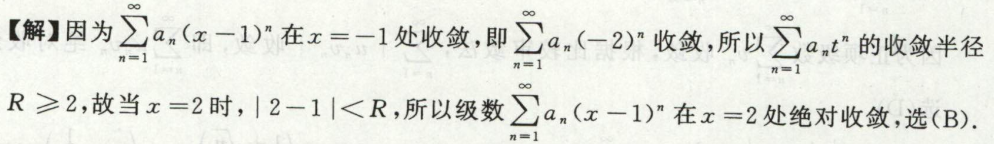
例8


例9
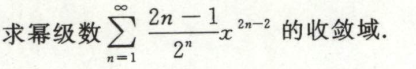

例10
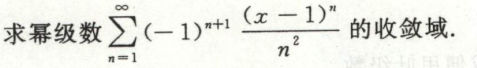

例11


求级数的和函数或和
根据级数收敛的定义,求级数的和
例1

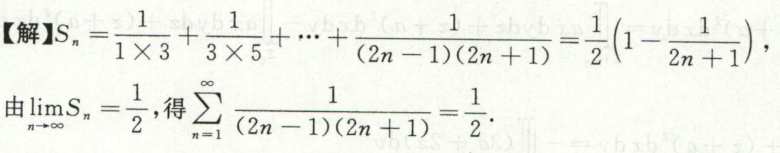
例2
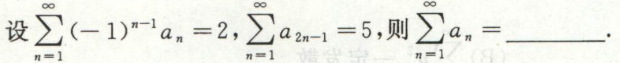

幂级数求和函数
幂级数求和函数之前,要先确定收敛域。
常见函数的麦克劳林级数:
| 函数 | 展开成麦克劳林级数(在\(x_0=0\)附近展开成级数) | 收敛域 |
|---|---|---|
| \(e^x\) | \(=1+x+ \frac{x^2}{2!} + ... + \frac{x^n}{n!} + ..\\ = \Sigma_{n=0}^{\infty} \frac{x^n}{n!}\) | \(-\infty<x<+\infty\) |
| \(\sin x\) | \(= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} +...\\ = \Sigma_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{2n+1}\) | \(-\infty<x<+\infty\) |
| \(\cos x\) | \(=1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ... \\ = \Sigma_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} x^{2n}\) | \(-\infty<x<+\infty\) |
| \(\frac{1}{1-x}\) | \(=1+x+x^2+x^3+... \\ = \Sigma_{n=0}^{\infty} x^n\) | \(-1<x<1\) |
| \(\frac{1}{1+x}\) | \(= \Sigma_{n=0}^{\infty} (-1)^n x^n\) | \(-1<x<1\) |
| \(ln(1+x)\) | \(=x-\frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + ... \\ = \Sigma_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} x^n\) 注意这个级数从n=1开始 | \(-1<x \le 1\) |
| \(-ln(1-x)\) | \(=x + \frac{x^2}{2} + \frac{x^3}{3} + \frac{x^4}{4} + ... \\ = \Sigma_{n=1}^{\infty} \frac{x^n}{n}\) 注意这个级数从n=1开始 | \(-1 \le x<1\) |
| \((1+x)^{m}\) | \(=1+m x+\frac{m(m-1)}{2 !} x^{2}+\cdots+\frac{m(m-1) \cdots(m-n+1)}{n !} x^{n}+\cdots\) 这个展开叫做二项展开式,也是代数学中的二项展开定理 | \((-1<x<1)\) |
例1

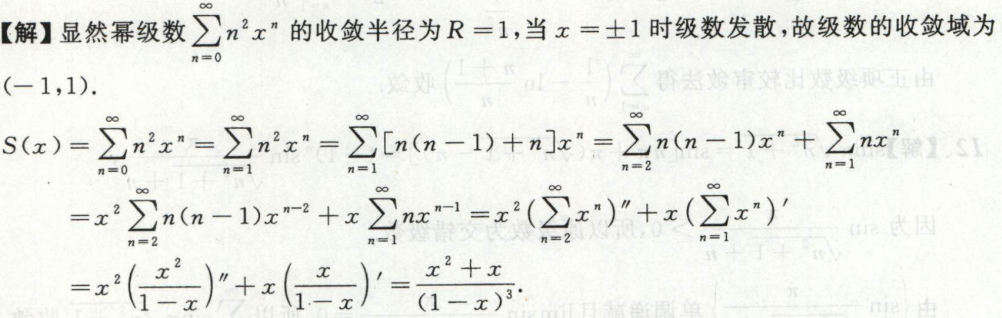
例2


例3


例4
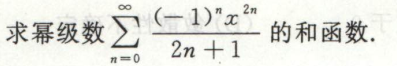

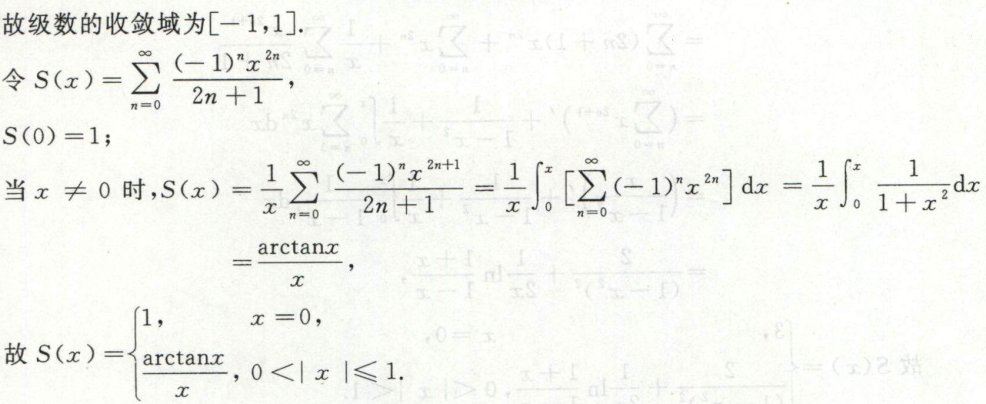
例5


例6
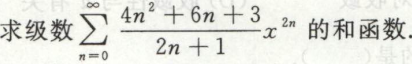

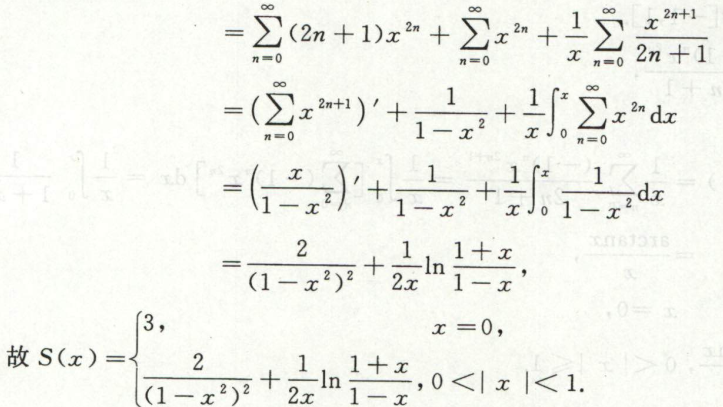
例7

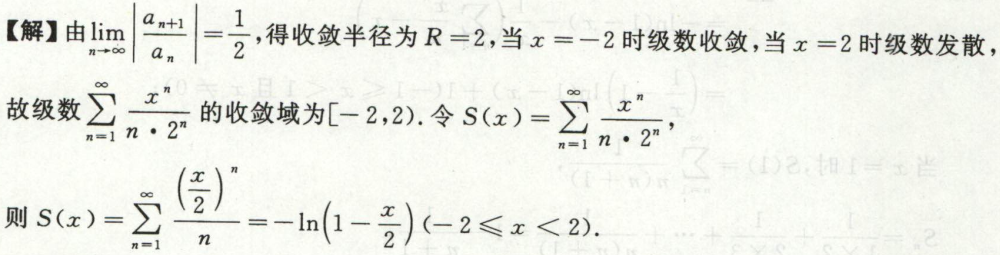
例8

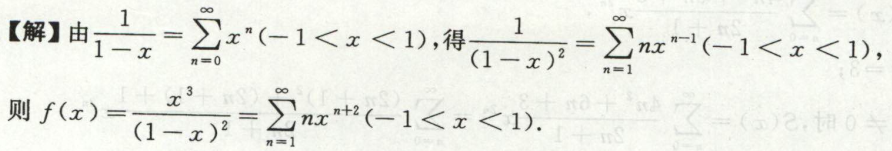
例9


例10


例11

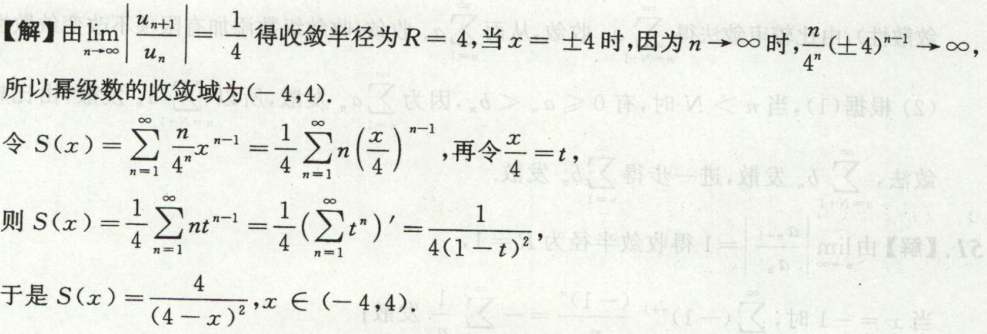
例12
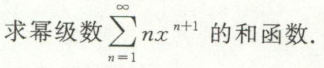

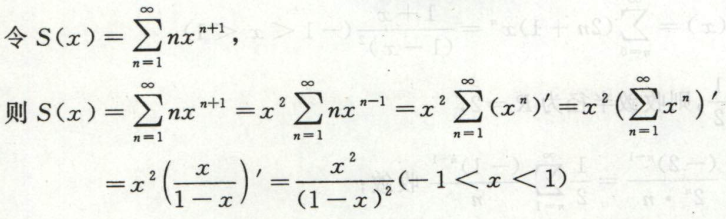
例13


例14


例15
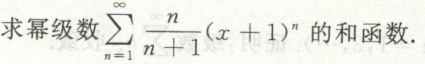

例16
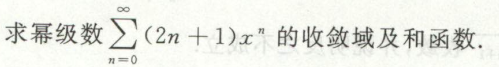

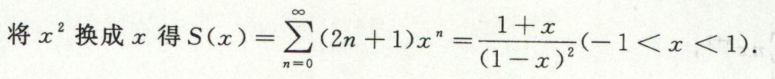
例17


例18 此题需要功底

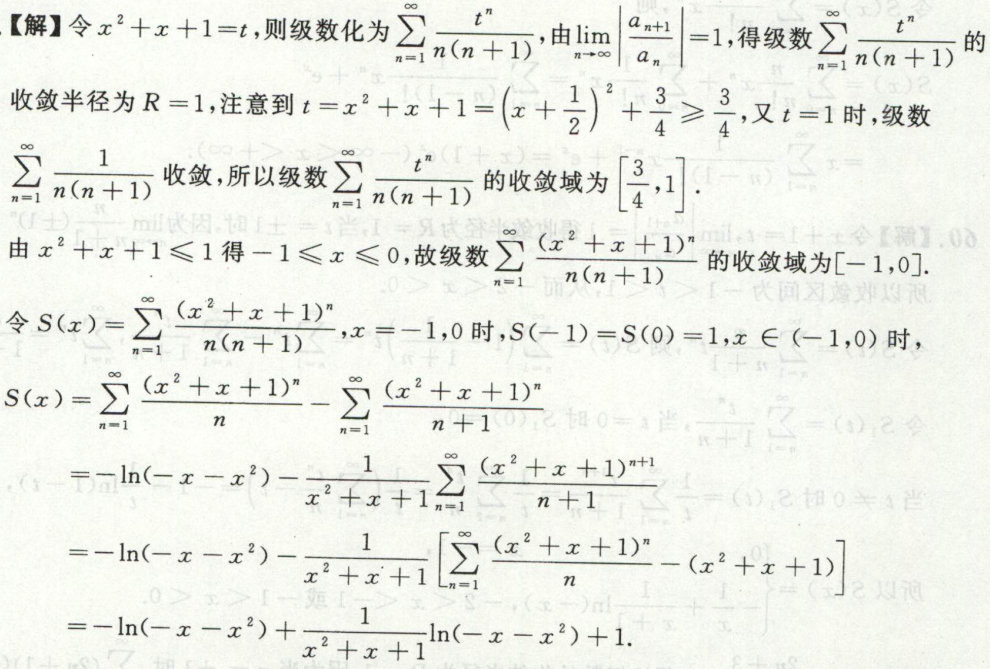
例19
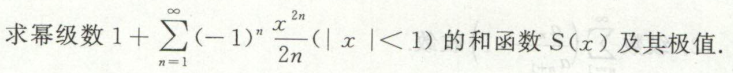

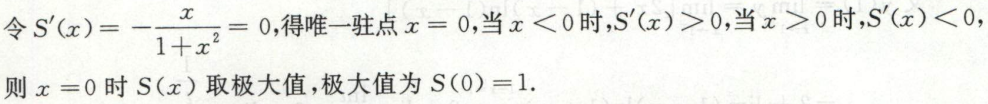
例20


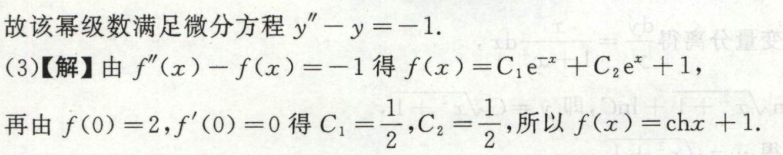
幂级数求和函数,再求级数的和
幂级数求和函数之前,要先确定收敛域。
例1


例2


例3


例4



例5 此题需要功底


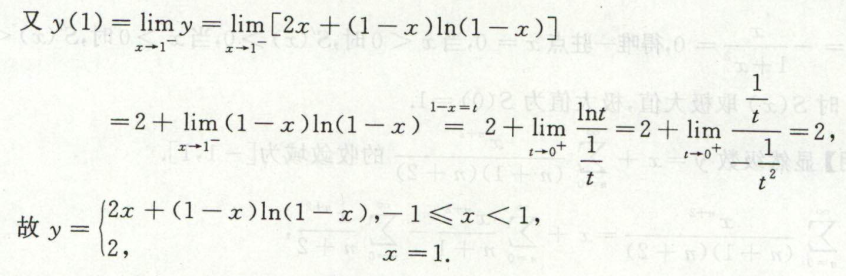
求傅里叶级数的和
例1


例2

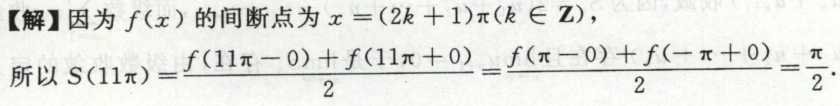
例3


函数展开成级数
函数展开成幂级数
函数展开成幂级数,有公式法(泰勒展开,展成泰勒级数)和间接法(借助基本函数的幂级数展开、逐项可导、可积性质的方法)。一般用间接法。展开成幂级数的同时一般要确定收敛域。
例1



例2

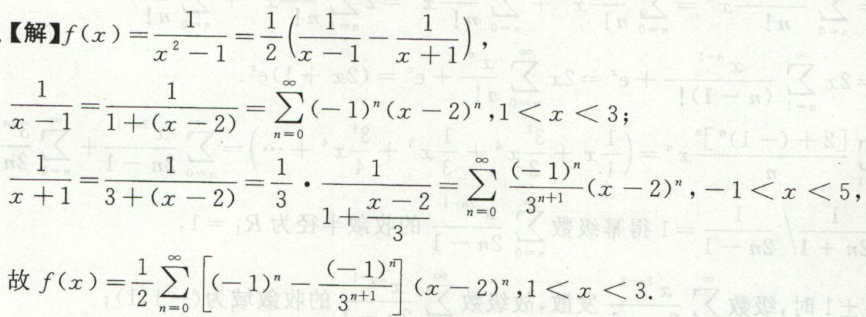
例3


例4


例5


例6

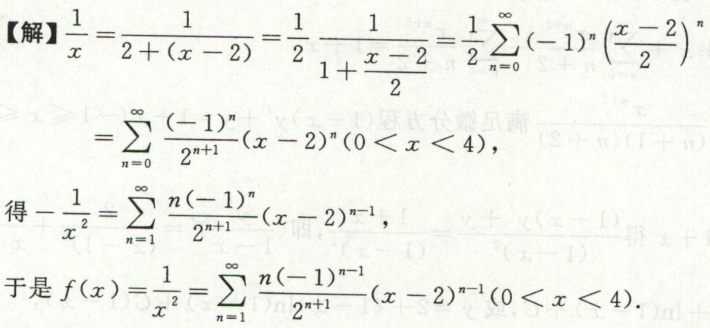
例7


例8


函数展开成傅里叶级数
例1


例2


例3

