数据结构总结

树

二叉树

二叉树搜索树

平衡二叉搜索树（AVL树）

参考：https://zhuanlan.zhihu.com/p/34899732 参考：https://oi-wiki.org/ds/avl/ 参考：https://www.jianshu.com/p/65c90aa1236d 参考：https://blog.csdn.net/wanderlustLee/article/details/81297253

AVL树是，在二叉搜索树的前提下，能保证平衡的树。

AVL树特点

  • 二叉搜索树的特点：对树上的任意节点，其左子树上的值都小于当前节点的值，其右子树上的值都大约当前节点的值
  • 平衡：对树上的任意节点，其左子树高度与右子树高度相差不超过1.（高度差可为-1，0，1）

AVL树的基本操作/功能

  • 二叉搜索树的操作：插入/删除/搜索，可能还包括找上一个/下一个节点
  • 维持树的平衡

维持树的平衡

平衡条件是什么？

对树上的任意节点，其左子树高度与右子树高度相差不超过1.（高度差可为-1，0，1）

什么原因会失去平衡，哪些节点会失去平衡？

假设当前的树已经平衡。当AVL树进行插入/删除操作时，可能造成某些节点左右子树高度的变动，破坏树的平衡。 具体的说，插入/删除位置的祖先节点可能会失去平衡。所以插入删除完成后，需要逆着查找路径，依次维护祖先节点的平衡性。

如何使失去平衡的某个节点恢复平衡？

我们要做的操作是，调整该节点处的左右子树高度，使其重新平衡。形象的描述就是要进行旋转操作，使其重新平衡。

左旋操作、右旋操作示意图：

img

实际上，一次旋转操作并不能保证使失去平衡的树恢复平衡。

不平衡情况

前面说了插入/删除节点可能导致祖先节点失去平衡。以插入节点为例（删除类似），祖先节点具体会有4种不平衡情况：LL、RR、LR、RL。下面具体说明。

在左孩子的左子树插入节点导致不平衡LL
批注 2020-06-11 144254

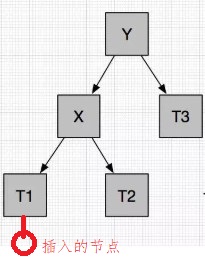
这种情况只需在失去平衡的节点Y处，进行一次左旋操作即可。

在右孩子的右子树插入节点导致不平衡RR
批注 2020-06-11 144827

这种情况只需在失去平衡的节点X处，进行一次右旋操作即可。

在左孩子的右子树插入节点导致不平衡LR
批注 2020-06-11 145834

这种情况需在失去平衡的节点的左子节点X处，先进行一次左旋操作，再在当前节点Y进行一次右旋操作即可。

在右孩子的左子树插入节点导致不平衡RL
批注 2020-06-11 150123

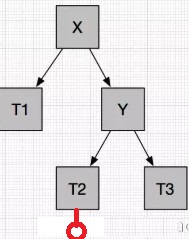
这种情况需在失去平衡的节点的右子节点处，先进行一次右旋操作，再在当前节点进行一次左旋操作即可。

java实现：（插入/删除和中序遍历）

package com.jingmin.datastructure;

import java.util.Scanner;
import java.util.Stack;

/**
 * @author : wangjm
 * @date : 2020/6/11 16:38
 * AVL树(插入/删除操作和中序遍历）
 * <p>
 * 参考（过程和逻辑）：https://zhuanlan.zhihu.com/p/34899732
 * 参考（类结构和部分实现）：https://blog.csdn.net/qq_25806863/article/details/74755131
 * 相关题目: https://www.nowcoder.com/pat/5/problem/4117
 * <p>
 * 注意：java里没有指针，在子节点的方法中，想修改父亲节点的对子节点的引用，需要借助递归+返回值
 */
public class AVLTree {
    /**
     * AVL树的根
     */
    Node1024 root;

    /**
     * 插入操作
     */
    public void insert(int n) {
        root = insert(root, n);
    }

    /**
     * 删除操作
     */
    public void delete(int n) {
        root = delete(root, n);
    }

    public static Node1024 insert(Node1024 node, int n) {
        if (node == null) {
            return new Node1024(n);
        }
        //递归插入
        if (n < node.value) {
            node.lChild = insert(node.lChild, n);
        } else if (n > node.value) {
            node.rChild = insert(node.rChild, n);
        }
        //使当前节点保持平衡
        // 注意，insert()是个递归函数，所以随后也逆着查找路径，逐级维护各祖先节点的平衡。
        node = reBalance(node);
        //更新当前节点高度(就算插入后仍然平衡，但是高度可能会改变）
        node.setHeight();
        return node;
    }

    public static Node1024 delete(Node1024 node, int n) {
        if (node == null) {
            return null;
        }
        //如果要删除的不是当前节点，递归去子节点删除
        if (n < node.value) {
            node.lChild = delete(node.lChild, n);
        } else if (n > node.value) {
            node.rChild = delete(node.rChild, n);
        } else {
            //如果删除的就是本节点，考虑本节点是叶子/单链/满分支
            if (node.lChild != null && node.rChild != null) {
                //满分支情况
                //去右子树找下一个节点(一定是个叶子），换到当前位置
                Node1024 min = node.rChild;
                while (min.lChild != null) {
                    min = min.lChild;
                }
                min.rChild = delete(node.rChild, min.value);
                min.lChild = node.lChild;
                node = min;
            } else {
                //单链/叶子情况
                node = (node.lChild != null) ? node.lChild : node.rChild;
            }
        }
        //叶子节点删掉就没了，不需要如下操作。
        if (node != null) {
            //重新平衡
            node = reBalance(node);
            //更新当前节点高度
            node.setHeight();
        }
        return node;
    }

    private static Node1024 reBalance(Node1024 node) {
        int factor = node.getFactor();
        if (factor > 1) {
            if (node.lChild.getFactor() > 0) {
                //LL不平衡情形，单次右旋
                node = rightRotate(node);
            } else {
                //LR不平衡情形，先左旋，再右旋
                node.lChild = leftRotate(node.lChild);
                node = rightRotate(node);
            }
        } else if (factor < -1) {
            if (node.rChild.getFactor() > 0) {
                //RL不平衡情形，先右旋，再左旋
                node.rChild = rightRotate(node.rChild);
                node = leftRotate(node);
            } else {
                //RR不平衡情形，单次左旋
                node = leftRotate(node);
            }
        }
        return node;
    }


    /**
     * 右旋操作
     */
    private static Node1024 rightRotate(Node1024 root) {
        //右旋操作
        Node1024 left = root.lChild;
        root.lChild = left.rChild;
        left.rChild = root;
        //更新高度(root旋转到了较下面的位置，要先更新高度）
        root.setHeight();
        left.setHeight();
        //返回新的上级节点
        return left;
    }

    /**
     * 左旋操作
     */
    private static Node1024 leftRotate(Node1024 root) {
        //左旋操作
        Node1024 right = root.rChild;
        root.rChild = right.lChild;
        right.lChild = root;
        //更新高度
        root.setHeight();
        right.setHeight();
        return right;
    }

    /**
     * 中序遍历
     */
    public String inOrderTraversal() {
        if (this.root == null) {
            return null;
        }
        Node1024 node = root;
        Stack<Node1024> stack = new Stack<>();
        StringBuilder sb = new StringBuilder();
        while (node != null || !stack.isEmpty()) {
            while (node != null) {
                stack.push(node);
                node = node.lChild;
            }
            if (!stack.isEmpty()) {
                node = stack.pop();
                sb.append(node.value).append(" ");
                node = node.rChild;
            }
        }
        if (sb.length() > 0) {
            sb.setLength(sb.length() - 1);
        }
        return sb.toString();
    }

    /**
     * 测试
     */
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        AVLTree tree = new AVLTree();
        for (int i = 0; i < n; i++) {
            tree.insert(scanner.nextInt());
        }
        scanner.close();
        System.out.println(tree.root.value);
//        System.out.println(tree.inOrderTraversal());
//        System.out.println("Delete 80:");
//        tree.delete(80);
//        System.out.println(tree.inOrderTraversal());
//        System.out.println("Delete 88:");
//        tree.delete(88);
//        System.out.println(tree.inOrderTraversal());
//        System.out.println("Delete 70:");
//        tree.delete(70);
//        System.out.println(tree.inOrderTraversal());
    }
}

/**
 * AVL树节点
 */
class Node1024 {
    int height;
    int value;
    Node1024 lChild, rChild;

    public Node1024(int value) {
        this.value = value;
        this.height = 1;
    }

    /**
     * 更新节点的高度
     */
    public void setHeight() {
        int lHeight = this.lChild == null ? 0 : this.lChild.height;
        int rHeight = this.rChild == null ? 0 : this.rChild.height;
        this.height = 1 + (lHeight > rHeight ? lHeight : rHeight);
    }

    /**
     * 计算平衡因子
     */
    public int getFactor() {
        int lHeight = this.lChild == null ? 0 : this.lChild.height;
        int rHeight = this.rChild == null ? 0 : this.rChild.height;
        return lHeight - rHeight;
    }
}

c++实现：（仅插入操作）

//来源：牛客网牛友提交的答案
//https://www.nowcoder.com/profile/4547010/codeBookDetail?submissionId=8196767
#include <iostream>
#include <cstdio>
#include <string>
using namespace std;
 
struct node
{
    int v,h;
    node *l,*r;
};
 
node tree[22];
int sum;
 
int H(node *a)
{
    return a?(a->h):(-1);
}
 
node *LL(node *k1)
{
    node *k2 = k1->l;
    k1->l = k2->r;
    k2->r = k1;
    k1->h = max(H(k1->l),H(k1->r))+1;
    k2->h = max(H(k2->l),H(k2->r))+1;
    return k2;
}
 
node *RR(node *k1)
{
    node *k2 = k1->r;
    k1->r = k2->l;
    k2->l = k1;
    k1->h = max(H(k1->l),H(k1->r))+1;
    k2->h = max(H(k2->l),H(k2->r))+1;
    return k2;
}
 
node *LR(node *k1)
{
    k1->l = RR(k1->l);
    return LL(k1);
}
 
node *RL(node *k1)
{
    k1->r = LL(k1->r);
    return RR(k1);
}
 
node *insertnode(node *root,int x)
{
    if(root==0)
    {
        root = &tree[sum++];
        root->l = root->r = 0;
        root->v = x;
        root->h = 0;
    }
    else if(x < root->v)
    {
        root->l = insertnode(root->l, x);
        if(H(root->l) - H(root->r)==2)
            root = (x < root->l->v)?LL(root):LR(root);
    }
    else
    {
        root->r = insertnode(root->r, x);
        if(H(root->r) - H(root->l)==2)
            root = (x > root->r->v)?RR(root):RL(root);
    }
    root->h = max(H(root->l), H(root->r))+1;
    return root;
}
 
int main()
{
    int n;
    node *root = 0;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        int x;
        scanf("%d",&x);
        root = insertnode(root,x);
    }
    printf("%d\n",root->v);
}

图

图的逻辑结构

图的存储结构

邻接矩阵

邻接表

邻接表将邻接矩阵的每行改为单链表存储,具有 n 个顶点,可以用 n 个单链表构成的链表数组存放。 每个 单链表链接一个顶点发出的所有边结点,链表长度即为对应的 顶点的度数。

邻接多重边表

邻接多重边表的存储结构不再以顶点为中心,而是以边为 中心。 每条边用一个边结点表示,每个边结点 包含两个端点信息、 和对应两个端点的下一条边结点的指针。 所需存储空间与邻接表相同,但是克服了边属性修改需要两次 的操作的问题。

半边数据结构

其他图的存储结构

三维网格

节点：三维网格的网格（或网格点）表示节点，用3维数组存储。

边：每个网格（或网格点）只和周围的6个网格（网格点）邻接。这样的存储结构只能包含边的邻接关系信息，不能包含权值信息。

可另外使用6个三维网格，单独存储每个网格（网格点）上下左右前后6条邻接边的权值信息。

三维网格模型的压缩存储CSR

CSR：compressed storage format

参考

散列

散列的概念

散列是一种算法（更像是一种思想）。

散列函数是将一系列输入映射到有限的存储空间的函数。

不同的输入可能会散列成相同的输出（发生碰撞/冲突），所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。

散列的存取过程

散列的存入操作

向散列映射的存储空间中存内容前，先计算散列函数/散列值/地址序标。 如果没有发生碰撞（即散列值对应的存储地址中还没有存入内容），直接向对应的存储地址中写入内容； 如果发生了碰撞，按下面几种处理冲突的方法，寻找新的存储地址，直到找到空着的存储地址，向其中写入内容。

散列的取出操作

与散列的存入过程类似，只是要注意，根据散列值/地址序标取内容时，要判断一下是未发生碰撞前存入的值，还是第几次碰撞的值，然后对应取出。

处理冲突的方法

参考：https://baike.baidu.com/item/hash/390310

参考：https://blog.csdn.net/zeb_perfect/article/details/52574915

开放寻址法

Hi=(H(key) + di) MOD m,i=1,2,…，k(k<=m-1)，其中H(key)为散列函数，m为散列表长，di为增量序列，可有下列三种取法：

1)． di=1,2,3,…，m-1，称线性探测再散列；

2)． di=12,-12,22,-22,32,…，±k2,(k<=m/2)称二次探测再散列；

3)． di=伪随机数序列，称伪随机探测再散列。

注：但是牛客网题目：平方探测的查找式子是(key + step * step) % size 而不是(key % size + step * step)%size

再散列法

Hi=RHi(key),i=1,2,…，k RHi均是不同的散列函数，即在同义词产生地址冲突时计算另一个散列函数地址，直到冲突不再发生，这种方法不易产生“聚集”，但增加了计算时间。

链地址法（拉链法）

HashMap 就是使用链地址法来解决冲突的（jdk8中采用平衡树来替代链表存储冲突的元素，但hash() 方法原理相同）。

img

拉链法的优缺点： 优点： ①拉链法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短； ②由于拉链法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况； ③开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而拉链法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间； ④在用拉链法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表，删除结点不能简单地将被删结 点的空间置为空，否则将截断在它之后填人散列表的同义词结点的查找路径。这是因为各种开放地址法中，空地址单元(即开放地址)都是查找失败的条件。因此在 用开放地址法处理冲突的散列表上执行删除操作，只能在被删结点上做删除标记，而不能真正删除结点。 缺点： 指针需要额外的空间，故当结点规模较小时，开放定址法较为节省空间，而若将节省的指针空间用来扩大散列表的规模，可使装填因子变小，这又减少了开放定址法中的冲突，从而提高平均查找速度。

建立一个公共溢出区

假设哈希函数的值域为[0,m-1],则设向量HashTable[0..m-1]为基本表，另外设立存储空间向量OverTable[0..v]用以存储发生冲突的记录。

树状数组

参考：https://zhuanlan.zhihu.com/p/25185969

参考*：https://oi-wiki.org/ds/fenwick/

树状数组可以用来求数组的区间和与前缀和。（虽然稍稍增加了单点修改的时间）

树状数组C[]

原始数组a[],其中各元素\(a_i\)是所需数据。

树状数组c[],其中各元素\(c_i\)管理了一定范围内的a[j:i]元素。

树状数组详细讲解，不会算法也能看懂哦~

c1 = a1 c2 = a1 + a2 c3 = a3 c4 = a1 + a2 + a3 + a4 c5 = a5 c6 = a5 + a6 c7 = a7 c8 = a1 + a2 + a3 + a4 + a5 + a6 + a7 + a8

c[1]管理的是a[1]； c[2] 管理的是a[1] & a[2] ； c[3]管理的是a[3]； c[4]管理的是a[1] & a[2] & a[3] & a[4]； c[5] 管理的是a[5]； c[6] 管理的是a[5] & a[6] ； c[7]管理的是 a[7]； c[8]管理的是 a[1] & a[2] & a[3] & a[4] & a[5] & a[6] & a[7] & a[8]；

\(c_i\)管理元素的个数

img

c[]中元素\(c_i\)具体管理了几个a[]中元素，由数组标号的二进制形式末尾0的个数决定。 例如， \(1_{(10)}=1_{(2)}\)末尾没有0，管理2^0=1个元素 \(2_{(10)}=10_{(2)}\)末尾1个0，管理2^1=2个元素 \(3_{(10)}=11_{(2)}\)末尾没有0，管理2^0=1个元素 \(4_{(10)}=100_{(2)}\)末尾2个0，管理2^2=4个元素 \(5_{(10)}=101_{(2)}\)末尾没有0，管理2^0=1个元素 \(6_{(10)}=110_{(2)}\)末尾1个0，管理2^1=2个元素 \(7_{(10)}=111_{(2)}\)末尾没有0，管理2^0=1个元素 \(8_{(10)}=1000_{(2)}\)末尾3个0，管理2^3=8个元素

那么怎么获取二进制数末尾0的个数？ 还记得计算机中原码和补码的相互转换吗？ 正数的原码和补码是相同的。 负数的原/补码转换有两种方法： 方法1：表示成2进制，按位取反（不包含符号位），最后再+1 方法2：表示成2进制，从末尾开始向高位，末尾的连续的0和第一个1不变，然后剩下的高位数字都取反（不包含符号位）

二进制负数的原码补码的相互转换方法2给了我们灵感。转换后高位都取反，中间1个1不变，低位都是0不变。

比如一个数n=4（带符号32位太长了，这里简单点用8位） n的原码（正数）：\(4_{(10)}=100_{(2)}=00000100_{(2)}\) n的补码：\(4_{(10)}=100_{(2)}=00000100_{(2)}\) -n的原码(负数）:\(-4_{(10)}=-100_{(2)}=10000100_{(2)}\) -n的补码: \(\text{补}[-4_{(10)}]=\text{补}[-100_{(2)}]=11111100_{(2)}\)

计算机中都是补码运算，相反数补码按位与，即n & (-n)，只保留了最低位开始的第1个1.从而得到了这个数二进制形式末尾0的个数，或者管理的元素个数。

回到树状数组，将此操作（相反数补码按位与）写成函数，用来获取\(c_i\)管理a[j:i]元素个数

int lowbit(int x) {
  // 算出x二进制的从右往左出现第一个1以及这个1之后的那些0组成数的二进制对应的十进制的数
  //相反数补码按位与
  return x & -x;
}

单点修改

由于我们没有维护a[]，而是维护了树状数组c[]，修改\(a_i\)对应于修改c[]中所有管理\(a_i\)的元素。

void add(int x, int k) {
  while (x <= n) {  // 不能越界
    c[x] = c[x] + k;
    x = x + lowbit(x);
  }
}

求前缀和

求前缀和a[1:i]，从c[i]对应的位置开始加，向靠近0的位置找管理不到的（找到上级就不管它的下级了）

int getsum(int x) {  // a[1]……a[x]的和
  int ans = 0;
  while (x >= 1) {
    ans = ans + c[x];
    x = x - lowbit(x);
  }
  return ans;
}

树状数组T1[], T2[]

区间修改&区间求和

原始数组a[],其中各元素\(a_i\)是所需数据。 假设数组b[]是a[]的差分数组，则\(a_i = \Sigma_{j=1}^i b_i\) ，也即b[]的前缀和为\(a_i\)

a[]的前缀和\(\Sigma_{i=1}^r a_i\)，经数学推导，可以表示为\(\Sigma_{i=1}^r b_i\)和\(\Sigma_{i=1}^r (i \cdot b_i)\)的线性运算，分别用b[]和d[]维护。证明：

\(\begin{array}{l} \sum_{i=1}^{r} a_{i} \\ =\sum_{i=1}^{r} \sum_{j=1}^{i} b_{j} \\ =\sum_{i=1}^{r} b_{i} \times(r-i+1) \\ =\sum_{i=1}^{r} b_{i} \times(r+1)-\sum_{i=1}^{r} b_{i} \times i \end{array}\)

即a[]的前缀和 可以用 b[]前缀和与d[]前缀和表示。 a[]的区间和也可以表示为两个前缀和的相减。

综上，a[]可以用其差分数组b[]表示，a[]的前缀和可以用b[]的前缀和与d[]的前缀和表示。

前面两节我们介绍了使用树状数组c[]表示a[]作单点修改和求前缀和。 那么我们同样可以用树状数组t1[],t2[]表示b[],d[]。

int t1[MAXN], t2[MAXN], n;

inline int lowbit(int x) { return x & (-x); }

void add(int k, int v) {
  int v1 = k * v;
  while (k <= n) {
    t1[k] += v, t2[k] += v1;
    k += lowbit(k);
  }
}

int getsum(int *t, int k) {
  int ret = 0;
  while (k) {
    ret += t[k];
    k -= lowbit(k);
  }
  return ret;
}

void add1(int l, int r, int v) {
  add(l, v), add(r + 1, -v);  // 将区间加差分为两个前缀加
}

long long getsum1(int l, int r) {
  return (r + 1) * getsum(t1, r) - 1 * l * getsum(t1, l - 1) -
         (getsum(t2, r) - getsum(t2, l - 1));
}

注意：现在已经无法直接获取到\(a_i\),只能求a[]在区间上的和。