数据结构-栈和队列
栈和队列

栈
基本概念
栈的定义
栈( Stack)只允许在一端进行插入或删除操作的线性表
后进先出(LIFO)
共享栈的定义
将两个栈底设置在共享空间的两端,栈顶向空间中间延伸
优点:存取时间复杂度仍为O(1),但空间利用更加有效
栈的基本操作
Initstack(&S):初始化一个空栈S StackEmpty(S):判断一个栈是否为空,若栈为空则返回true,否则返回 False。 Push(&S,x):进栈,若栈S未满,则将x加入使之成为新栈顶。 Pop(&S,&x):出栈,若栈非空,则弹出栈顶元素,并用×返回。 GetTop(s,&x):读栈顶元素,若栈非空则用×返回栈顶元素。 ClearStack(&S):销毁栈,并释放S占用的内存空间。
存储结构
顺序存储
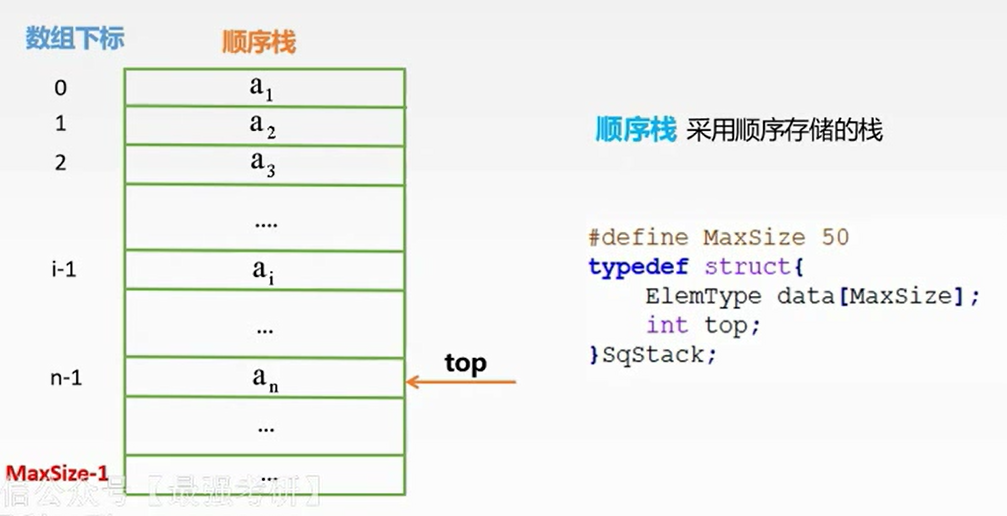





而对于共享栈:

链式存储

所有的操作都在表头进行。入栈出栈对应于单链表在表头的插入和删除,判空也与单链表相同。
栈的应用
括号匹配
表达式求值
中缀表达式转后缀式1
中缀表达式转后缀表达式主要有两种方法
- 根据中缀表达式,写出表达式树,然后后序遍历,即得到后缀表达式(去掉括号的输出)。
- 读取中缀表达式,直接输出操作数,利用栈保存操作符。向栈中保存操作符前,栈中优先级高的操作符要先输出/参与运算。这样得到的输出也是后缀表达式。
例如,中缀表达式a + bc + (d e + f) * g,其转换成后缀表达式则为a b c * + d e * f + g * +。
中缀表达式转换后缀表达式过程:使用栈(保存操作符)的方法,具体过程如下:
- 如果遇到操作数,我们就直接将其输出(加入到后缀表达式)。
- 如果遇到操作符,(栈中优先级高的操作符要先输出/参与运算,再把当前操作符入栈)
- 若为’(’,直接入栈
- 若为’)‘,则依次把栈中的运算符输出(加入到后缀表达式),直到出现’(‘,并从栈中删除’(’; 注意,左括号只弹出并不输出。
- 若为’+‘,’-‘,’*‘,’,‘/’
- 若高于栈顶元素优先级,或栈空,或栈顶为’(’,直接入栈;
- 否则,先依次弹出栈顶运算符,直到一个优先级比它低的运算符或’(‘为止; 弹出完这些元素后,才将遇到的操作符压入到栈中。 有一点需要注意,只有在遇到" ) "的情况下我们才弹出’(‘,其他情况我们都不会弹出’(’。
- 如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
public class CalcExpr {
/**
* 操作符,优先级由高到低
*/
public final static String[][] OPERATORS = new String[][]{new String[]{"("}, new String[]{"*", "/"},
new String[]{"+", "-"}, new String[]{")"}};
/**
* 中缀表达式转后缀表达式
*/
private static String exprInOrder2PostOrder(String expr) {
if (expr == null) {
return null;
}
//保存后缀表达式输出结果
StringBuilder sb = new StringBuilder();
//符号栈(保存表达式中的操作符)
Stack<String> stack = new Stack();
//输入字符串分隔为多个token
Tokens tokens = new Tokens(expr);
//顺序操作每个token
while (tokens.hasNext()) {
String token = tokens.next();
//如果是操作符
if (isOperator(token)) {
//栈非空,且栈顶不是'(',且当前符号优先级不高于栈顶操作符时
while (!stack.empty() && !"(".equals(stack.peek()) && !isOperatorGreater(token, stack.peek())) {
sb.append(stack.pop()).append(" ");
}
//符号入栈。如果遇到的是")",则不需要入栈,且需弹出"("
if (")".equals(token)) {
stack.pop();
} else {
stack.push(token);
}
}
//如果是操作数(也可能是字母表示的操作数)
else {
sb.append(token).append(" ");
}
}
while (!stack.isEmpty()) {
sb.append(stack.pop()).append(" ");
}
return sb.toString();
}
/**
* 判断是否为操作符
*/
private static boolean isOperator(String ch) {
for (String[] chars : OPERATORS) {
for (String c : chars) {
if (ch.equals(c)) {
return true;
}
}
}
return false;
}
/**
* 判断参数ch1的优先级是否高于ch2
*/
private static boolean isOperatorGreater(String ch1, String ch2) {
int level1 = -1, level2 = -1;
for (int i = 0; i < OPERATORS.length; i++) {
for (int j = 0; j < OPERATORS[i].length; j++) {
if (ch1 != null && ch1.equals(OPERATORS[i][j])) {
level1 = i;
}
if (ch2 != null && ch2.equals(OPERATORS[i][j])) {
level2 = i;
}
}
}
if (level1 != -1 && level2 != -1 && level1 < level2) {
return true;
}
return false;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
String expr = scanner.nextLine();
System.out.println(exprInOrder2PostOrder(expr));
scanner.close();
}
}
/**
* 根据分隔符划分为多个token,包含分隔符
*/
class Tokens {
private String originStr;
private String[] tokens;
/**
* 分隔符默认是加减乘除小括号
*/
private String spliters = "\\+|-|\\*|/|\\(|\\)";
private int index;
public Tokens(String originStr) {
this.originStr = originStr;
this.tokens = null;
index = 0;
split();
}
private void split() {
if (originStr != null) {
tokens = originStr.split("(?<=(" + spliters + "))|(?=(" + spliters + "))");
}
}
public boolean hasNext() {
if (originStr != null && index < tokens.length) {
return true;
}
return false;
}
public String next() {
return tokens[index++].trim();
}
}递归
若在一个函数、过程或数据结构的定义中又应用了它自身,则称它为递归定义的,简称递归
单链表节点的定义,计算斐波那契数的递归实现,都算作递归。
递归的精髓在于能否将原始问题转换为属性相同但规模较小的问题。

递归函数
递归函数的两个必要条件是递归表达式和递归出口。

递归调用的问题
在递归调用过程中,系统为每一层的返回点、局部变量、传入实参等开辟了递归工作栈来迸行数据存储,递归次数过多容易造成栈溢出。
通常情况下递归的效率并不高

递归转换为非递归
递归算法转换为非递归算法,有的可以直接用循环实现,有的需要用到栈。
队列
基本概念
队列的定义
队列( Queue)只允许在表的一端进行插入,表的另一端进行删除操作的线性表
先进先出(FIFO)
队列的基本操作
InitQueue(&Q):初始化队列,构造一个空队列Q QueueEmpty(Q):判队列空,若队列Q为空返回true,否则返回 false。 En Queue(&Qx):入队,若队列Q末满,则将x加入使之成为新的队尾。 De queue(&Q&x):出队,若队列Q非空,则删除队头元素,并用x返回Gethead(Q&x):读队头元素,若队列Q非空则用x返回队头元素。 Clear Queue(&Q):销毁队列,并释放队列Q占用的内存空间。
存储结构
顺序存储

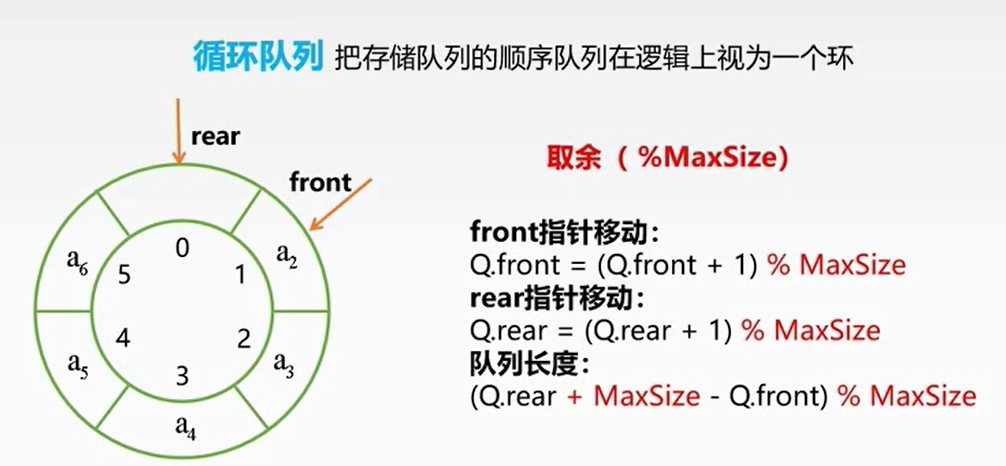
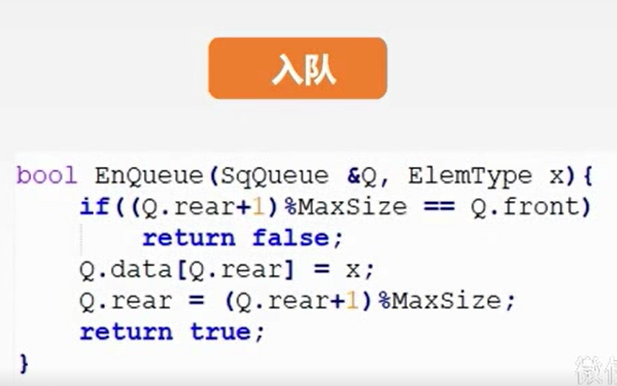
判断队空队满:






链式存储
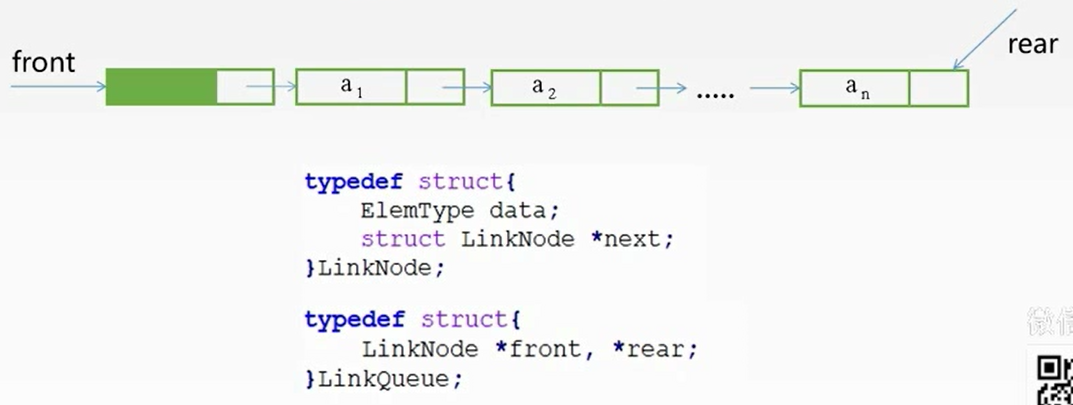
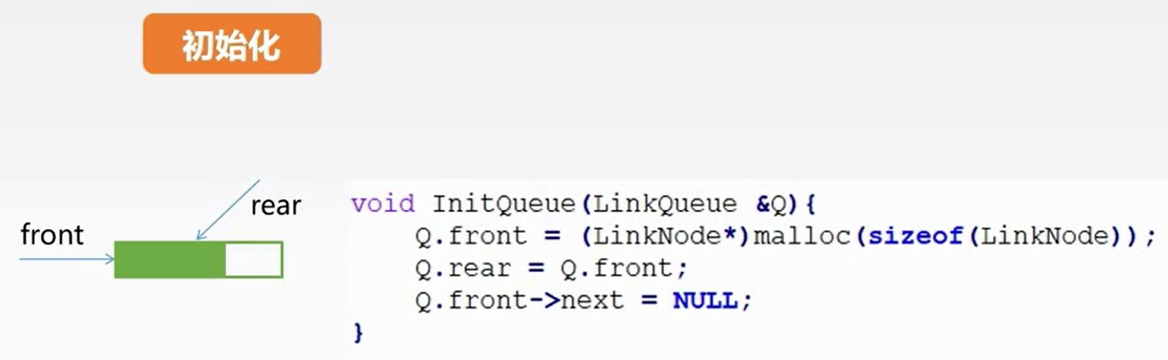


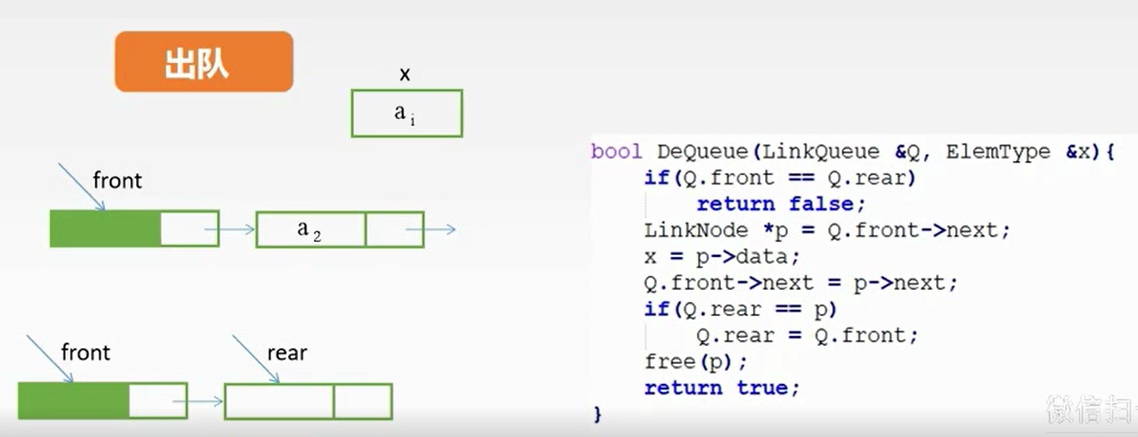
注:如果初始化时rear为null,可以省略最后的判断
队列的应用
层次遍历
计算机系统
双端队列
出栈序列和出队序列
连续输入和连续输出

栈的非连续输入和输出

合法规则
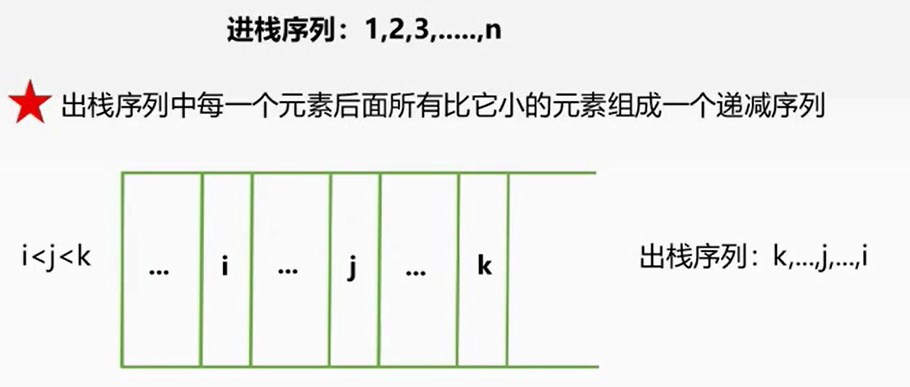
合法出栈序列个数

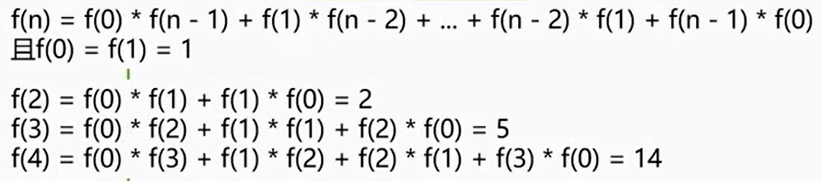

双端队列
双端队列:允许两端都可以进行入队以及出队操作的队列

输入受限的双端队列
输入受限的双端队列,屏蔽一端的输出操作,可变成栈。所以栈的所有合法输出序列,在该输入受限的双端队列中都是合法的。
输出受限的双端队列
输出受限的双端队列,屏蔽一端的输入操作,可变成栈。所以栈的所有合法输出序列,在该输出受限的双端队列中都是合法的。
数组
数组的定义
这里的数组是指”数组”这种逻辑结构,不单指C语言中的数组实现。
数组(逻辑结构)是由n(n>=1)个相同类型的数据元素构成的有限序列,每个数据元素称为一个数组壳素,每个元素受n个线性关系的约束,每个元素在n个线性关系中的序号称为该元素的下标,并称该数组为n维数组。
数组是线性表的推广。数组相当于n维的、大小固定的线性表。 线性的顺序存储,使用的就是1维的数组的实现(1维数组的存储结构)。
数组的特点
数组有维度
常见一维数组和二维数组
数组的维度和维界不可变
数组一旦被定义,其维度和维界不可变,数组除初始化和销毁外,只有存取元素和修改元素的操作
数组的存储结构
行优先存储
例如,二维数组\(a[m][n]\),寻址其中的元素\(a_{ij}\), \(Address(a_{ij}) = Address(a_{00})+(m*i+j)*NODE_SIZE\)
列优先存储
矩阵的压缩存储
矩阵是数学中的叫法,其实就是二维数组,只不过数据结构的二维数组序标从0开始,矩阵的序标从1开始。
压缩存储是指迻多个值相同的元素只分配一个存储空间,对零元素不分配存储空间。
一些特殊矩阵可以进行压缩存储,这里的特殊矩阵指:具有许多相同矩阵元素或零元素,并且这些相同矩阵元素或零元素的分布有一定规律性的矩阵。
对称矩阵的压缩存储
按行优先存储时,矩阵(二维数组)压缩存储到一个一维数组中,下标对应关系如下(矩阵下标从1开始)

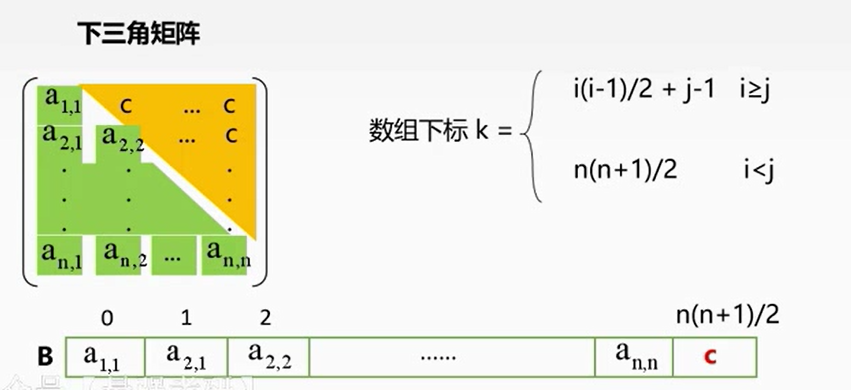
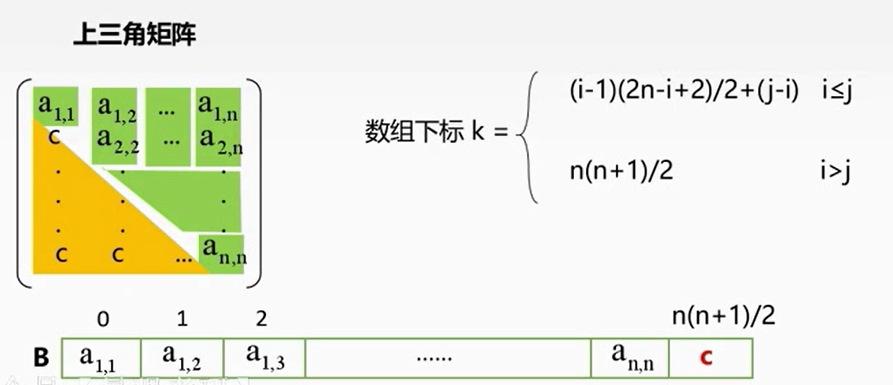
三角矩阵的压缩存储
注意矩阵下标从1开始

三对角矩阵的压缩存储
注意矩阵下标从1开始

稀疏矩阵的压缩存储
稀疏矩阵使用三元组(行标,列标,值)来压缩存储
稀疏矩阵压缩存储后失去了随机存储的特性

CSDN「石锅拌饭」原文链接:https://blog.csdn.net/sgbfblog/java/article/details/8001651↩︎