PAT甲级习题
PAT甲级习题
栈的模拟
例1
已知入栈顺序1-N,并给定栈最大容积M。判断出栈顺序是否正确, 以及是否爆栈
方法:栈的模拟
由于入栈是固定从1到N的,那么某元素出栈前,比它小的数都应当已经入栈。利用这个过程来确定出入栈顺序。
package com.jingmin.advanced2;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Stack;
/**
* @author : wangjm
* @date : 2020/6/26 09:55
* @discription : https://www.nowcoder.com/pat/5/problem/4090
* 已知入栈顺序,判断出栈顺序是否正确, 以及是否爆栈: 栈的模拟
* 由于入栈是固定从1到N的,那么某元素出栈前,比它小的数都应当已经入栈
*/
public class Advanced1040 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] s = br.readLine().split(" ");
int m = Integer.parseInt(s[0]);
int n = Integer.parseInt(s[1]);
int k = Integer.parseInt(s[2]);
int[] test = null;
int index;
Stack<Integer> stack = new Stack<>();
while (k-- > 0) {
stack.clear();
test = new int[n];
s = br.readLine().split(" ");
for (int i = 0; i < n; i++) {
test[i] = Integer.parseInt(s[i]);
}
index = 1;
for (int i = 0; i < n; i++) {
while (stack.isEmpty() || test[i] > stack.peek()) {
stack.push(index++);
}
if (test[i] != stack.peek() || stack.size() > m) {
break;
} else {
stack.pop();
}
}
if (stack.isEmpty() && --index == n) {
System.out.println("YES");
} else {
System.out.println("NO");
}
}
br.close();
}
}
还有牛客网牛友在讨论区贴出的代码,更简洁
//链接:https://www.nowcoder.com/questionTerminal/597a931ab1794139835ad2991faeab2d
//来源:牛客网 北航闫子浩
#include<stdio.h>
int main()
{
int M,N,K,a[1001],i,j,l;
char c[2];
scanf("%d %d %d",&M,&N,&K);//M为栈长,N为数组长,K为组数
while(K--){
for(i=j=l=0;i<N;i++){//l为当前栈长,j为最近入栈的数
scanf("%d",a);
while(l<M&&a[0]>j)a[++l]=++j;
if((l==M&&a[0]>j)||a[l--]<a[0])i=N;
}
gets(c);
printf(i>N?"NO\n":"YES\n");
}
}
例2
已知二叉树中序遍历非递归的栈操作顺序,求该树的后序遍历。
方法:模拟栈操作可以获得中序遍历序列,另外注意所有 Push 的节点组成的序列就是这棵树的先序遍历序列。于是问题转为从一棵树的先序遍历序列和中序遍历序列生成这棵树。
所以可以参考:算法总结.md#树的遍历#由前序和中序遍历重建二叉树
package com.jingmin.advanced;
import java.util.*;
/**
* @author : wangjm
* @date : 2020/2/4 14:27
* @discription : https://www.nowcoder.com/pat/1/problem/4314
* <p>
* 中序遍历序列可以模拟出栈操作获得,另外注意所有 Push 的节点组成的序列就是这棵树的先序遍历序列。
* 于是问题转为从一棵树的先序遍历序列和中序遍历序列生成这棵树。
*/
public class Advanced1004_2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
List<BinaryTree> preOrderList = new ArrayList<>(8);
List<BinaryTree> inOrderList = new ArrayList<>(8);
Stack<BinaryTree> stack = new Stack<>();
for (int i = 0; i < 2 * n; i++) {
String action = scanner.next();
if ("Push".equals(action)) {
BinaryTree node = new BinaryTree(scanner.nextInt());
stack.push(node);
preOrderList.add(node);
} else if ("Pop".equals(action)) {
inOrderList.add(stack.pop());
}
}
scanner.close();
BinaryTree root = rebuildBinaryTree(preOrderList, inOrderList);
System.out.println(root.postOrderTraversal().trim());
}
/**
* 由前序遍历和中序遍历重建二叉树
* <p>
* 参考: https://zhuanlan.zhihu.com/p/37265145
*/
public static BinaryTree rebuildBinaryTree(List<BinaryTree> preOrderList, List<BinaryTree> inOrderList) {
for (int i = 0; i < preOrderList.size(); i++) {
if (preOrderList.get(0).equals(inOrderList.get(i))) {
preOrderList.get(0).left = rebuildBinaryTree(preOrderList.subList(1, i + 1), inOrderList.subList(0, i));
preOrderList.get(0).right = rebuildBinaryTree(preOrderList.subList(i + 1, preOrderList.size()),
inOrderList.subList(i + 1, inOrderList.size()));
return preOrderList.get(0);
}
}
return preOrderList.isEmpty() ? null : preOrderList.get(0);
}
static class BinaryTree {
BinaryTree left;
BinaryTree right;
private int index;
private UUID uuid = UUID.randomUUID();
public BinaryTree(int index) {
this.index = index;
}
public String postOrderTraversal() {
return (left == null ? "" : left.postOrderTraversal())
+ (right == null ? "" : right.postOrderTraversal())
+ index + " ";
}
@Override
public boolean equals(Object object) {
return this.uuid.equals(((BinaryTree)object).uuid);
}
@Override
public String toString() {
return this.index+ "";
}
}
}
树的深度
例1
供应商问题
供应商,经销商,零售商组成多级供应链。每经过一级,价格提高一定比率。
给出每个节点的父亲序号,求最高价格,以及最高价格零售商有几个。
方法1:BFS树的广度优先/层次遍历
/**
* 树形结构:层次遍历找最深的点(本代码实现的方式)
*/
public class Advanced1003 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
double p = scanner.nextDouble();
double r = scanner.nextDouble();
Node1003[] nodes = new Node1003[n];
for (int i = 0; i < n; i++) {
nodes[i] = new Node1003(i);
}
//构造树
Node1003 root = null;
for (int i = 0; i < n; i++) {
int father = scanner.nextInt();
if (father != Const1003.UNDEFINED) {
nodes[father].children.add(nodes[i]);
} else {
root = nodes[i];
}
}
scanner.close();
System.out.println(LFS(root, p, r));
}
//层次遍历,返回最深层次的价格,以及最深层节点数
private static String LFS(Node1003 root, double price, double rate) {
double retPrice = 0;
int retNum = -1;
Queue<Node1003> queue = new LinkedList<Node1003>();
queue.add(root);
int levelSize = 1;
int level = 0;
while (!queue.isEmpty()) {
int count = 0;
for (int i = 0; i < levelSize; i++) {
Node1003 node = queue.poll();
node.price = price;
if (!node.children.isEmpty()) {
queue.addAll(node.children);
count += node.children.size();
}
}
level++;
retPrice = price;
retNum = levelSize;
price *= 1 + rate * 0.01;
levelSize = count;
}
return String.format("%.2f %d", retPrice, retNum);
}
}
//节点类
class Node1003 {
int id;
double price;
List<Node1003> children;
public Node1003(int id) {
this.id = id;
this.price = Const1003.UNDEFINED;
this.children = new ArrayList<>();
}
}
//常量定义
class Const1003 {
public static final int UNDEFINED = -1;
}
方法2:DFS深度优先遍历
类似上一种方法,牛客网牛友提交的讨论代码:
//链接:https://www.nowcoder.com/questionTerminal/24429a3319e4466790e65a647130b118
//来源:牛客网
//爆搜dfs
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=1e5+5;
int n,root,anscnt=0;double p,r;
vector<int> G[maxn];
map<int,int> mp;
void dfs(int cur,int step){
int ok=1;
for(int i=0;i<G[cur].size();++i){
int v=G[cur][i];ok=0;
dfs(v,step+1);
}
if(ok){
if(step>anscnt){
anscnt=step;++mp[anscnt];return ;
}
if(step==anscnt){
++mp[anscnt];return ;
}
}
}
int main(){
scanf("%d %lf %lf",&n,&p,&r);
for(int i=0,tmp;i<n;++i){
scanf("%d",&tmp);
if(tmp==-1){ root=i;continue;}
G[tmp].push_back(i);
}
dfs(root,0);
printf("%.2f %d\n",p*pow(1+r*0.01,anscnt),mp[anscnt]);
return 0;
}
方法3:枚举
//牛客网牛友提交的代码
//https://www.nowcoder.com/profile/1701726/codeBookDetail?submissionId=10247559
#include <stdio.h>
#include <math.h>
#define MAXN 100000
int main()
{
int N;
double P, R;
scanf("%d", &N);
scanf("%lf", &P);
scanf("%lf", &R);
int shit[MAXN];
for (int i = 0; i < N; i++)
{
scanf("%d", &shit[i]);
}
int maxlevel = 0, templevel = 0, maxnum = 0;
int end;
for (int i = 0; i < N; i++)
{
end = i;
while (shit[end] != -1)
{
templevel++;
end = shit[end];
}
if (templevel > maxlevel)
{
maxlevel = templevel;
maxnum = 1;
}
else if (templevel == maxlevel)
maxnum++;
templevel = 0;
}
double max;
max = P * pow(1 + (R / 100.0), maxlevel);
printf("%.2f %d", max, maxnum);
}
方法4:枚举优化:保存搜索过的答案
其实是对枚举时的操作做了优化:保存搜索过的内容,下次搜索就不用向下搜索了
/**
* 或者使用数组,记录father[]和price[],level[]信息,循环查找各点的价钱和层次,注意保存一下搜索过的答案(本代码使用的方法)
*/
public class Advanced1003_2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
double p = scanner.nextDouble();
double r = scanner.nextDouble();
int[] father = new int[n];
for (int i = 0; i < n; i++) {
father[i] = scanner.nextInt();
}
int[] level = new int[n];
int maxLevel = 0;
int maxLevelCount = 0;
int thisLevel = 0;
//枚举找最深层,并记录个数
for (int i = 0; i < n; i++) {
thisLevel = getLevel(father, level, i);
if (thisLevel > maxLevel) {
maxLevel = thisLevel;
maxLevelCount = 1;
} else if (thisLevel == maxLevel) {
maxLevelCount++;
}
}
scanner.close();
System.out.println(String.format("%.2f %d", p * Math.pow(1 + r * 0.01, maxLevel - 1), maxLevelCount));
}
/**
* 递归获取level方法(同时保存计算结果,方便重复使用)
*/
private static int getLevel(int[] father, int[] level, int i) {
if (father[i] == -1) {
level[i] = 1;
} else {
if (level[father[i]] != 0) {
level[i] = level[father[i]] + 1;
} else {
level[i] = getLevel(father, level, father[i]) + 1;
}
}
return level[i];
}
}
还可以将上面获取level的递归函数改为非递归函数
//牛客网牛友提交的代码,不过确实是这个思路
//https://www.nowcoder.com/profile/6639688/codeBookDetail?submissionId=6510475
#include <stdio.h>
#include <math.h>
int main()
{
int n, s[100001], g[100001] = {0}, i, t, c, mc = 0, x, m = 0;
double p, r;
scanf( "%d", &n );
scanf( "%lf%lf", &p, &r );
for( i = 0; i < n; i ++ )
scanf( "%d", s + i );
for( i = 0; i < n; i ++ ){
if( !g[i] ){
t = i, c = 0;
while( t >= 0 && !g[t] ){
c ++;
t = s[t];
}
if( t >= 0 ) //g[t]前面已经求过
x = g[t] + c;
else
x = c;
//判断当前深度
if( x > m )
mc = 1, m = x;
else if( x == m )
mc ++;
//储存结果
t = i;
while( t >= 0 && !g[t] ) g[t] = x --, t = s[t];
}
}
printf( "%.2lf %d\n", p * pow( 1 + r / 100, m - 1.0 ), mc );
return 0;
}
例2
族谱中人最多的一代
给定某一族谱,找族谱中人最多的一代,以及这一代的人数。
方法一:穷举
链接:https://www.nowcoder.com/questionTerminal/324faf954885435ba3b1c9bbd2a7a81e
来源:牛客网YuanYuan的讨论
#include <stdio.h>
#include <malloc.h>
int get_gen(int *family, int child) {
int gen = 1;
while (family[child] != child) {
gen++;
child = family[child];
}
return gen;
}
int main() {
int N, M;
scanf("%d %d", &N, &M);
int *family = (int *) malloc((N + 1) * sizeof(int));
for (int i = 0; i <= N; ++i) {
family[i] = i;
}
for (int i = 0; i < M; ++i) {
int parent;
int child_num;
scanf("%d %d", &parent, &child_num);
for (int j = 0; j < child_num; ++j) {
int child;
scanf("%d", &child);
family[child] = parent;
}
}
int *gen = (int *) malloc((N + 1) * sizeof(int));
for (int i = 0; i <= N; ++i) {
gen[i] = 0;
}
for (int i = 1; i <= N; ++i) {
gen[get_gen(family, i)]++;
}
int max_gen = 0, max_member = 0;
for (int i = 1; i <= N; ++i) {
if (gen[i] > max_member) {
max_member = gen[i];
max_gen = i;
}
}
printf("%d %d", max_member, max_gen);
free(family);
free(gen);
return 0;
}
方法二:DFS
package com.jingmin.advanced2;
import java.util.*;
/**
* @author : wangjm
* @date : 2020/5/27 16:34
* @discription: https://www.nowcoder.com/pat/5/problem/4318
* <p>
* 从树中找节点数最多的那一层,以及那一层的节点数
* dfs (本代码实现的方法)
*/
public class Advanced1005 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
Map<String, Node1005> map = new HashMap<>(16);
//建map,建树
for (int i = 0; i < m; i++) {
String id = scanner.next();
Node1005 father = map.get(id);
if (father == null) {
father = new Node1005(id);
map.put(id, father);
}
int childrenNum = scanner.nextInt();
for (int j = 0; j < childrenNum; j++) {
id = scanner.next();
Node1005 child = map.get(id);
if (child == null) {
child = new Node1005(id);
map.put(id, child);
}
father.children.add(child);
}
}
scanner.close();
ArrayList<Integer> list = new ArrayList<>();
dfs(map.get("01"), 1, list);
int maxCount = 0;
int level = 0;
for (int i = 0; i < list.size(); i++) {
int count = list.get(i);
if (count > maxCount) {
maxCount = count;
level = i + 1;
}
}
System.out.println(maxCount + " " + level);
}
/**
* 递归dfs
*/
private static void dfs(Node1005 root, int level, List<Integer> list) {
if (list.size() >= level) {
list.set(level - 1, list.get(level - 1) + 1);
} else {
list.add(1);
}
for (Node1005 node : root.children) {
dfs(node, level + 1, list);
}
}
}
class Node1005 {
String id;
List<Node1005> children;
public Node1005(String id) {
this.id = id;
this.children = new ArrayList<>();
}
}
方法三:BFS
package com.jingmin.advanced2;
import java.util.*;
/**
* @author : wangjm
* @date : 2020/5/27 16:34
* @discription: https://www.nowcoder.com/pat/5/problem/4318
* <p>
* 从树中找节点数最多的那一层,以及那一层的节点数
* bfs (本代码的方法)
*/
public class Advanced1005_2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
Map<String, Node1005_2> map = new HashMap<>(16);
//建map,建树
for (int i = 0; i < m; i++) {
String id = scanner.next();
Node1005_2 father = map.get(id);
if (father == null) {
father = new Node1005_2(id);
map.put(id, father);
}
int childrenNum = scanner.nextInt();
for (int j = 0; j < childrenNum; j++) {
id = scanner.next();
Node1005_2 child = map.get(id);
if (child == null) {
child = new Node1005_2(id);
map.put(id, child);
}
father.children.add(child);
}
}
scanner.close();
System.out.println(bfs(map.get("01")));
}
/**
* bfs
*/
private static String bfs(Node1005_2 root) {
int maxLevel = 0;
int maxCount = 0;
Queue<Node1005_2> queue = new LinkedList<>();
queue.add(root);
int level = 1;
int levelSize = queue.size();
while (levelSize > 0) {
//判断当前层节点是否最多
if (levelSize > maxCount) {
maxCount = levelSize;
maxLevel = level;
}
//下一层节点入队
for (int i = 0; i < levelSize; i++) {
Node1005_2 node = queue.poll();
if (!node.children.isEmpty()) {
queue.addAll(node.children);
}
}
level++;
levelSize = queue.size();
}
String res = maxCount + " " + maxLevel;
return res;
}
}
class Node1005_2 {
String id;
List<Node1005_2> children;
public Node1005_2(String id) {
this.id = id;
this.children = new ArrayList<>();
}
}
优化:使用二维数组或list数组保存树
//牛客网牛友提交的代码,使用二维数组保存树
//https://www.nowcoder.com/profile/4739176/codeBookDetail?submissionId=11875064
#include "iostream"
using namespace std;
int main(){
int member[103][103]; //存放输入成员的下一代成员编号
int n,m;
cin>>n>>m;
//输入
for(int i=0;i<m;i++){
int id,ct;
cin>>id>>ct;
for(int j=0;j<ct;j++){
int temp;
cin>>temp;
member[id][0]++;
member[id][member[id][0]]=temp;
}
}
//最大的数量和该层数
int maxcount=1,maxlayer=1;
//按辈分存放成员,从1开始 ,fmlfree[i][0]用于存放该辈的成员数量
int fmltree[103][103];
fmltree[1][0]=1;
fmltree[1][1]=1;
//逐层向fmltree添加成员
for(int layer=1;;layer++){
int count=0;
for(int i=1;i<=fmltree[layer][0];i++){
fmltree[layer+1][0]+=member[fmltree[layer][i]][0];
for(int j=1;j<=member[fmltree[layer][i]][0];j++){
count++;
//向下一层添加本层成员的每个下一代
fmltree[layer+1][count]=member[fmltree[layer][i]][j];
}
}
//更新maxcount和maxlayer
if(count>maxcount){
maxcount=count;
maxlayer=layer+1;
}
if(count==0)break;
}
//输出
cout<<maxcount<<" "<<maxlayer;
return 0;
}
树的构造
例1
已知二叉搜索树的所有输入,要求生成一个二叉搜索树,且为完全二叉树。(生成的二叉搜索树不一定要与输入顺序对应)
题目最后要求层次遍历输出此树。
方法1:(引用/非数组)按层次建树,中序遍历写值
(引用/非数组)按层次建树,中序遍历写值
package com.jingmin.advanced2;
import java.util.*;
/**
* @author : wangjm
* @date : 2020/6/9 21:21
* @discription : https://www.nowcoder.com/pat/5/problem/4115
* 建立二叉搜索树,且要求为完全二叉树(唯一),然后层次遍历输出
* <p>
* 按层次建树,中序遍历写值,再层次遍历取值
*/
public class Advanced1022 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = scanner.nextInt();
}
scanner.close();
Arrays.sort(a);
//建树
Node1022 root = setupCompleteBinaryTree(n);
//中序遍历,向树中对应位置写值
ArrayList<Node1022> inOrdrList = inOrderTraversal(root);
for (int i = 0; i < n; i++) {
inOrdrList.get(i).value = a[i];
}
//层次遍历输出
ArrayList<Node1022> levelOrderList = bfs(root);
StringBuilder sb = new StringBuilder();
for (Node1022 node : levelOrderList) {
sb.append(node.value).append(" ");
}
sb.setLength(sb.length() - 1);
System.out.println(sb);
}
/**
* 层次建树,初始化一个n个节点的完全二叉树(n>=1)
* 注意,这个二叉树只建立起结构,没有存入值
*/
private static Node1022 setupCompleteBinaryTree(int n) {
int count = 0;
Node1022 root = new Node1022();
Queue<Node1022> queue = new LinkedList<>();
queue.add(root);
count++;
while (!queue.isEmpty() && count < n) {
Node1022 node = queue.poll();
if (count < n) {
node.lChild = new Node1022();
queue.add(node.lChild);
count++;
}
if (count < n) {
node.rChild = new Node1022();
queue.add(node.rChild);
count++;
}
}
return root;
}
/**
* 中序遍历
*/
private static ArrayList<Node1022> inOrderTraversal(Node1022 node) {
ArrayList<Node1022> list = new ArrayList<>();
Stack<Node1022> stack = new Stack<>();
while (!stack.isEmpty() || node != null) {
while (node != null) {
stack.push(node);
node = node.lChild;
}
node = stack.pop();
list.add(node);
node = node.rChild;
}
return list;
}
/**
* 层次遍历
*/
private static ArrayList<Node1022> bfs(Node1022 root) {
ArrayList<Node1022> list = new ArrayList<>();
Queue<Node1022> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node1022 node = queue.poll();
list.add(node);
if (node.lChild != null) {
queue.add(node.lChild);
}
if (node.rChild != null) {
queue.add(node.rChild);
}
}
return list;
}
}
class Node1022 {
int value;
Node1022 lChild, rChild;
}
方法2:二叉树的数组存储,中序递归建树写值
package com.jingmin.advanced2;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
/**
* @author : wangjm
* @date : 2020/6/9 23:22
* @discription: https://www.nowcoder.com/pat/5/problem/4115
* 建立二叉搜索树且为完全二叉树
* <p>
* 考虑二叉树的数组存储结构,数组的优点是随机访问,方便建树。
* 所有的值都填到数组的前面,则对应的二叉树是完全二叉树。
* 数组的顺次访问,对应的就是二叉树的层次遍历
*/
public class Advanced1022_2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] a = new int[n];
int[] tree = new int[n];
for (int i = 0; i < n; i++) {
a[i] = scanner.nextInt();
}
scanner.close();
Arrays.sort(a);
//中序遍历建树
ArrayList<Integer> inOrderList = new ArrayList<>();
inOrderTraversal(tree, 0, inOrderList);
for (int i = 0; i < n; i++) {
tree[inOrderList.get(i)] = a[i];
}
//层次遍历输出
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++) {
sb.append(tree[i]).append(" ");
}
sb.setLength(sb.length() - 1);
System.out.println(sb);
}
private static void inOrderTraversal(int[] tree, int node, List<Integer> list) {
int lChild = (node << 1) + 1;
int rChild = lChild + 1;
if (lChild < tree.length) {
inOrderTraversal(tree, lChild, list);
}
list.add(node);
if (rChild < tree.length) {
inOrderTraversal(tree, rChild, list);
}
}
}
最短路径问题
路径最短,累计值最小/最大,平均值最小最大
例1
公共自行车问题
从源点出发到某点去摆放自行车,经过路径节点上的自行车都要调整为半满。 要找最短路径; 若存在多条最短路径,则选出发前带的自行车最少的路径; 若还是存在多条路径,则选带回去最少自行车的路径。
方法1:穷举
方法2:DFS回溯
不是我写的,看人家思路就好
#include <iostream>
#include <vector>
#include <limits.h>
using namespace std;
void dfs(int start, int index, int end);
int cmax, N, sp, M;
int costTimes, outBikes, inBikes;
int resultTimes = INT_MAX;
int resultOutBikes, resultInBikes;
vector<int> bikes, path, resultPath;
vector<vector<int> > times;
vector<bool> visited;
int main()
{
ios::sync_with_stdio(false);
// 输入数据
cin >> cmax >> N >> sp >> M;
bikes.resize(N+1, 0);
visited.resize(N+1, false);
times.resize(N+1, vector<int>(N+1, 0));
for(int i=1; i<=N; i++) {
cin >> bikes[i];
}
int m, n, dist;
for(int i=0; i<M; i++) {
cin >> m >> n >> dist;
times[m][n] = dist;
times[n][m] = dist;
}
// 深搜并输出结果
dfs(0, 0, sp);
cout << resultOutBikes << " 0";
for(int i=1; i<resultPath.size(); i++) {
cout << "->" << resultPath[i];
}
cout << " " << resultInBikes;
return 0;
}
void dfs(int start, int index, int end)
{
// 访问
visited[index] = true;
path.push_back(index);
costTimes += times[start][index];
// 处理
if(index == end) {
// 计算这条路上带去的车和带回的车
inBikes = 0, outBikes = 0;
for(int i=1; i<path.size(); i++) {
if(bikes[path[i]] > cmax/2) {
inBikes += bikes[path[i]] -cmax/2;
} else {
if((cmax/2 - bikes[path[i]]) < inBikes) {
inBikes -= (cmax/2 - bikes[path[i]]);
} else {
outBikes += (cmax/2 - bikes[path[i]]) - inBikes;
inBikes = 0;
}
}
}
// 判断这条路是否更好
if(costTimes != resultTimes) {
if(costTimes < resultTimes) {
resultTimes = costTimes;
resultPath = path;
resultOutBikes = outBikes;
resultInBikes = inBikes;
}
} else if(outBikes != resultOutBikes) {
if(outBikes < resultOutBikes) {
resultPath = path;
resultOutBikes = outBikes;
resultInBikes = inBikes;
}
} else if(inBikes < resultInBikes) {
resultPath = path;
resultOutBikes = outBikes;
resultInBikes = inBikes;
}
} else {
// 递归
for(int i=1; i<=N; i++) {
if(times[index][i] != 0 && !visited[i]) {
dfs(index, i, end);
}
}
}
// 回溯
visited[index] = false;
path.pop_back();
costTimes -= times[start][index];
}
另有人写的,有点像dfs的非递归形式,也可能算动态规划:
//https://www.nowcoder.com/profile/156003592/codeBookDetail?submissionId=54952529
#include <cstdio>
#include <iostream>
#include <queue>
#include <utility>
using namespace std;
#define INF 0x3f3f3f3f
struct Edge{
int from;
int to;
int cost;
vector<int> trace;
Edge(int from_, int to_, int cost_):
from(from_), to(to_), cost(cost_), trace(){}
};
bool operator >(const Edge& lhs, const Edge& rhs){
return lhs.cost > rhs.cost;
}
int main(){
int C_max, N, sp, M;
cin >> C_max >> N >> sp >> M;
int perfect = C_max / 2;
vector<int> ss(N + 1);
for(int i = 1; i <= N; i++){
cin >> ss[i];
}
vector<vector<Edge>> graph(N + 1);
for(int i = 0; i < M; i++){
int s1, s2, t;
cin >> s1 >> s2 >> t;
graph[s1].emplace_back(s1, s2, t);
graph[s2].emplace_back(s2, s1, t);
}
vector<int> dist(N + 1, INF);
priority_queue<Edge, deque<Edge>, greater<Edge>> pq;
vector<vector<int>> paths;
Edge e(0, 0, 0);
e.trace.push_back(0);
pq.push(e);
while(!pq.empty()){
Edge e = pq.top(); pq.pop();
if(e.cost > dist[sp]) break;
if(e.cost > dist[e.to]) continue;
dist[e.to] = e.cost;
if(e.to == sp){
paths.push_back(e.trace);
}
for(auto& ne : graph[e.to]){
int ncost = e.cost + ne.cost;
if(ncost > dist[ne.to]) continue;
Edge ee(e.from, ne.to, ncost);
ee.trace = e.trace;
ee.trace.push_back(ne.to);
pq.push(ee);
}
}
pair<int, int> opt(INF, INF);
int idx = -1;
int ans_sent, ans_back;
for(int i = 0; i < (int)paths.size(); i++){
int current = 0;
int tot = 0;
auto& path = paths[i];
for(int j = 1; j < (int)path.size(); j++){
int d = ss[path[j]] - perfect;
current += d;
if(current < 0){
tot += -current;
current = 0;
}
}
if(make_pair(tot, current) < opt){
opt = make_pair(tot, current);
idx = i;
ans_sent = tot;
ans_back = current;
}
}
printf("%d ", ans_sent);
for(int v : paths[idx]){
if(v != 0) printf("->");
printf("%d", v);
}
printf(" %d", ans_back);
puts("");
}
方法3:保存各种状态Dijkstra算法
主要的状态:
bikes[]保存各点需要调整的自行车数
D[]保存从源点到各点的最短距离
need[]保存各点需要的自行车数
back[]保存各点需要带回的自行车数
visited[]保存各点是否已找到最短距离
trace[]记录到各点最短路径上,该点的前一个节点号
过程:
从源点开始,
根据D、need、back选最合适的点加入到已visited集,并更新未visited点的D、need、back、trace
重复上一步的步骤,直到点都加入visited集。
(注意:更新need、back值时要根据路径上前一点累计计算)
过程例子:
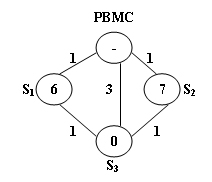
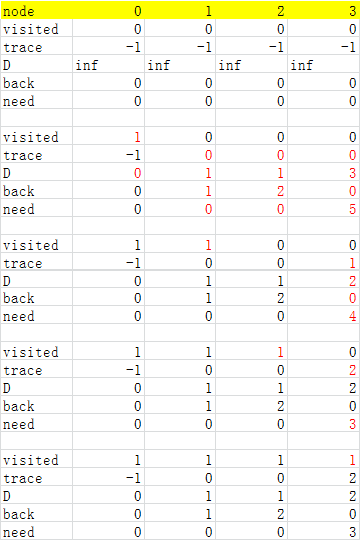
代码:
package com.jingmin.advanced2;
import java.util.*;
/**
* @author : wangjm
* @date : 2020/3/17 17:30
* @discription : https://www.nowcoder.com/pat/5/problem/4324
* <p>
* 图上起点到终点路径的距离最短,要求子路径距离最短
* 在各段最短子路径上,要求运去/need的车最少(每段累加)
* 在各段最短子路径上,运去的车need最少的前提下,要求运回的车最少
* <p>
* 参考:https://www.nowcoder.com/profile/1011153/codeBookDetail?submissionId=8013527
*/
public class Advanced1001 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int c = scanner.nextInt();
int n = scanner.nextInt();
int sp = scanner.nextInt();
int m = scanner.nextInt();
//每个顶点上多出的自行车数
int[] bikes = new int[n + 1];
//代表了边及上面的权值
Roads roads = new Roads(n + 1);
for (int i = 1; i <= n; i++) {
bikes[i] = scanner.nextInt();
bikes[i] -= (c / 2);
}
for (int i = 1; i <= m; i++) {
int a = scanner.nextInt();
int b = scanner.nextInt();
int v = scanner.nextInt();
roads.setRoad(a, b, v);
roads.setRoad(b, a, v);
}
scanner.close();
System.out.println(dijkstra(bikes, c, roads, sp));
}
/**
* dijkstra单源点最短路径算法,固定源点是顶点0
*/
private static String dijkstra(int[] bikes, int capacity, Roads roads, int dest) {
int[] D = new int[bikes.length];
//记录路径上到达每个顶点的前一个顶点
int[] trace = new int[bikes.length];
int[] need = new int[bikes.length];
int[] back = new int[bikes.length];
boolean[] visited = new boolean[bikes.length];
for (int i = 0; i < bikes.length; i++) {
D[i] = Const.INFTY;
}
Arrays.fill(trace, -1);
D[0] = 0;
int min = 0;
while (min != -1) {
//标记已加入最短集
visited[min] = true;
//更新与之相关的非最短集
for (Map.Entry<Integer, Integer> entry : roads.getRoadsOfNode(min).entrySet()) {
//对于边(i,j,v):顶点i与j存在一条边,距离是v,对应这里roads[i].entry(j,v)
int j = entry.getKey();
int v = entry.getValue();
if (!visited[j]) {
if (D[min] + v < D[j]) {
//找最短路径
D[j] = D[min] + v;
trace[j] = min;
//在此基础上,带来和送回的自行车数目要累加(优化过的结果为:)
back[j] = back[min] + bikes[j];
need[j] = need[min];
if (back[j] < 0) {
need[j] -= back[j];
back[j] = 0;
}
} else if (D[min] + v == D[j]) {
//先把算出来的值临时用n存起来,和之前的need比较
int b = back[min] + bikes[j];
int n = need[min];
if (b < 0) {
n -= b;
b = 0;
}
if (n < need[j] || (n == need[j] && b < back[j])) {
trace[j] = min;
back[j] = b;
need[j] = n;
}
}
}
}
//从非最短集中找最短
min = -1;
int minD = Const.INFTY;
int minNeed = Const.INFTY;
int minBack = Const.INFTY;
for (int i = 1; i < bikes.length; i++) {
if (!visited[i]) {
boolean isDisLess = D[i] < minD;
boolean isNeedLess = D[i] == minD && need[i] < minNeed;
boolean isBackLess = D[i] == minD && need[i] == minNeed && back[i] < minBack;
if (isDisLess || isNeedLess || isBackLess) {
min = i;
minD = D[i];
minNeed = need[i];
minBack = back[i];
}
}
}
}//dijkstra完成
StringBuilder sb = new StringBuilder();
sb.append(need[dest]).append(" ");
Stack<Integer> stack = new Stack();
stack.push(dest);
int i = dest;
while(trace[i] != -1) {
stack.push(trace[i]);
i = trace[i];
}
while (!stack.isEmpty()) {
sb.append(stack.pop()).append("->");
}
sb.setLength(sb.length() - 2);
sb.append(" ").append(back[dest]);
return sb.toString();
}
}
class Roads {
int nodeNum;
HashMap<Integer, Integer>[] roads;
public Roads(int nodeNum) {
this.nodeNum = nodeNum;
this.roads = new HashMap[nodeNum];
for (int i = 0; i < nodeNum; i++) {
roads[i] = new HashMap<>(8);
}
}
public int getRoad(int i, int j) {
Integer res = this.roads[i].get(j);
return res == null ? Const.INFTY : res;
}
public void setRoad(int i, int j, int value) {
this.roads[i].put(j, value);
this.roads[j].put(i, value);
}
public HashMap<Integer, Integer> getRoadsOfNode(int i) {
return this.roads[i];
}
}
class Const {
public static final int INFTY = Integer.MAX_VALUE / 2;
}
优化后的过程:
题目要求: 找距离最短(首要),从源点带来的自行车最少(次要),带回去的自行车最少(次次要)的路径。 合并带来最少和带回去最少的要求,则要求cost最小。 (cost为正时表时要带来的数量,为负时绝对值代表要带回去的数量。) (比如某两条路径距离都最短,第一条路径cost为正,需要带来自行车;第二条路径cost为负,需要带回去自行车,带来的自行车为0,那么选第二条路径)
则题目变成: 找距离最短(首要),cost最小(次要)的路径。 即多重最短/最小值问题。
这样的问题,只要在原生的Dijkstra算法中,判断首要最短的语句后,加上次要最小的判断即可。
优化后的代码:
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
void dijkstra(int &n, int &cmax, vector<vector<int>> &map, vector<int> &bikeNum, int endV) {
vector<bool> visited(n + 1, false);
vector<int> dist(n + 1, INT_MAX);
vector<int> cost(n + 1, 0);
vector<int> preV(n + 1, -1);
dist[0] = 0;
visited[0] = true;
cost[0] = 0;
int u = 0;
for (int i = 1; i <= n; i++) {
int minDist = INT_MAX;
for (int j = 0; j <= n; j++) {
if (!visited[j] && dist[j] < minDist) {
minDist = dist[j];
u = j;
}
}
visited[u] = true;
for (int j = 0; j <= n; j++) {
if (!visited[j] && map[u][j] < INT_MAX) {
if (dist[j] > dist[u] + map[u][j]) {
dist[j] = dist[u] + map[u][j];
cost[j] = cost[u] + cmax - bikeNum[j];
preV[j] = u;
} else if (dist[j] == dist[u] + map[u][j]) {
if (cost[j] > cost[u] + cmax - bikeNum[j]) {
cost[j] = cost[u] + cmax - bikeNum[j];
preV[j] = u;
}
}
}
}
}
int p = endV;
int nums[501], size = 0, minBike = 0;
for (int i = 0; i < n; i++) {
if (preV[p] == -1) {
break;
}
if (cost[p] + minBike > 0) {
minBike = -cost[p];
}
nums[size++] = p;
p = preV[p];
}
printf("%d 0", -minBike);
for (int i = size - 1; i >= 0; i--) {
printf("->%d", nums[i]);
}
if (cost[endV] + minBike> 0) {
printf(" 0\n");
} else printf("% d\n", -minBike-cost[endV]);
}
int main(int argc, const char * argv[]) {
int cmax, n, endv, m;
scanf("%d %d %d %d", &cmax, &n, &endv, &m);
vector<int> bikeNum(n + 1);
bikeNum[0] = 0;
for (int i = 1; i <= n; i++) {
scanf("%d", &bikeNum[i]);
}
vector<vector<int>> map(n + 1, vector<int> (n + 1, INT_MAX));
for (int i = 0; i < m; i++) {
int u, v;
scanf("%d %d", &u, &v);
scanf("%d", &map[u][v]);
map[v][u] = map[u][v];
}
int c = cmax/2;
dijkstra(n, c, map, bikeNum, endv);
return 0;
}
例2
条条大路通罗马问题
指定出发城市,去到罗马。 要求路径最短; 次要要求总愉悦值最大(每经过一个城市都会带来一定程度的愉悦感); 次次要要求平均愉悦值最大(总愉悦值相同时,考虑平均愉悦值,那么要求经过城市越少越好)
方法1:保存各种状态的Dijkstra算法
过程:
初始化各种状态(各点的累计距离值、累计快乐值、步数值) 从源点开始,挑选累计距离值最小(首要)、累计快乐值最大(次要)、步数值最小(次次要)的点,进行visited 更新没有visited各点的距离值、累计快乐值最、步数值最小 重复上面个两步,直到所有点都visited
过程例子:
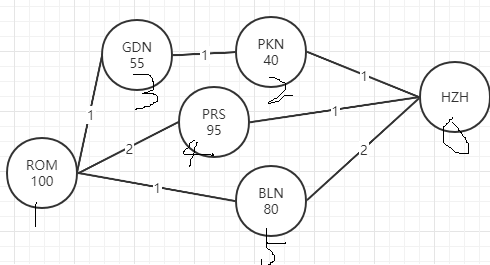
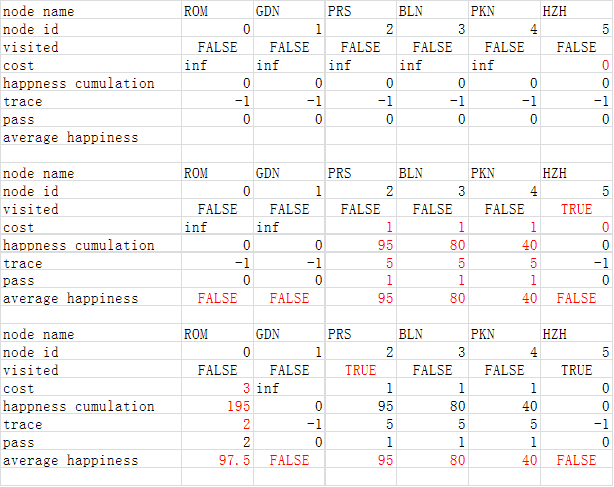
编写代码:
package com.jingmin.advanced2;
import java.util.Arrays;
import java.util.HashMap;
import java.util.Scanner;
import java.util.Stack;
/**
* @author : wangjm
* @date : 2020/5/19 17:25
* @discription: https://www.nowcoder.com/pat/5/problem/4315
* <p>
* 要求路径最短,累加值最大,平均值最大(或步数最少)
* 这里用Dijkstra算法,(代码已实现)
* 还可以使用优先队列优化dijkstra算法中循环找最小的过程(这里的代码没有实现优化)
*/
public class Advanced1002 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
String startName = scanner.next();
City1002[] citys = new City1002[n];
citys[0] = new City1002(0, startName, 0);
HashMap<String, Integer> nameIdMap = new HashMap<>(8);
nameIdMap.put(startName, 0);
for (int i = 1; i < n; i++) {
City1002 city = new City1002(i, scanner.next(), scanner.nextInt());
citys[i] = city;
nameIdMap.put(city.name, city.id);
}
int[][] roads = new int[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(roads[i], Const1002.INFTY);
}
for (int i = 0; i < k; i++) {
String c1 = scanner.next();
String c2 = scanner.next();
int cost = scanner.nextInt();
roads[nameIdMap.get(c1)][nameIdMap.get(c2)] = cost;
roads[nameIdMap.get(c2)][nameIdMap.get(c1)] = cost;
}
scanner.close();
System.out.println(dijkstra2Rom(citys, roads, nameIdMap));
}
private static String dijkstra2Rom(City1002[] citys, int[][] road, HashMap<String, Integer> nameIdMap) {
int[] cost = new int[citys.length];
int[] happiCumu = new int[citys.length];
boolean[] visited = new boolean[citys.length];
int[] trace = new int[citys.length];
int[] pass = new int[citys.length];
int[] minCostCount = new int[citys.length];
Arrays.fill(cost, Const1002.INFTY);
Arrays.fill(trace, Const1002.NONE);
Arrays.fill(minCostCount, 1);
cost[0] = 0;
for (int i = 0; i < citys.length; i++) {
//没visited的点中按优先级找距离最小、快乐和最大、平均快乐最大的点
int minCost = Const1002.INFTY;
int maxHappiCumu = 0;
int minStep = Const1002.INFTY;
int k = Const1002.NONE;
for (int j = 0; j < citys.length; j++) {
if (!visited[j]) {
//首要cost最小,次要happiCumu最大,次次要averHapp最大/步数最少
if (cost[j] < minCost) {
k = j;
minCost = cost[j];
maxHappiCumu = happiCumu[j];
minStep = pass[j];
} else if (cost[j] == minCost) {
if (happiCumu[j] > maxHappiCumu) {
k = j;
maxHappiCumu = happiCumu[j];
minStep = pass[j];
} else if (happiCumu[j] == maxHappiCumu) {
if (pass[j] < minStep) {
k = j;
minStep = pass[j];
}
}
}
}
}
if (k == Const1002.NONE) {
break;
}
//访问该点
visited[k] = true;
//更新未访问点的各种状态
for (int j = 0; j < citys.length; j++) {
if (!visited[j]) {
int costThroughK = cost[k] + road[k][j];
int happiThroughK = happiCumu[k] + citys[j].happiness;
int stepThoughK = pass[k] + 1;
boolean changeRoute = false;
if (costThroughK < cost[j]) {
changeRoute = true;
minCostCount[j] = minCostCount[k];
} else if (costThroughK == cost[j]) {
minCostCount[j] += minCostCount[k];
boolean happiMore = happiThroughK > happiCumu[j];
boolean stepLess = happiThroughK == happiCumu[j] && stepThoughK < pass[j];
if (happiMore || stepLess) {
changeRoute = true;
}
}
if (changeRoute) {
trace[j] = k;
cost[j] = costThroughK;
happiCumu[j] = happiThroughK;
pass[j] = stepThoughK;
}
}
}
}
StringBuilder sb = new StringBuilder();
int romId = nameIdMap.get("ROM");
sb.append(minCostCount[romId]).append(" ")
.append(cost[romId]).append(" ")
.append(happiCumu[romId]).append(" ")
.append(happiCumu[romId] / pass[romId]).append("\n");
Stack<Integer> stack = new Stack<>();
while (romId != Const1002.NONE) {
stack.push(romId);
romId = trace[romId];
}
while (!stack.isEmpty()) {
sb.append(citys[stack.pop()].name).append("->");
}
sb.setLength(sb.length() - 2);
return sb.toString();
}
}
class City1002 {
int id;
String name;
int happiness;
public City1002(int id, String name, int happiness) {
this.id = id;
this.name = name;
this.happiness = happiness;
}
}
class Const1002 {
public final static int INFTY = Integer.MAX_VALUE / 2;
public final static int NONE = -1;
}
方法2:Dijkstra找最短,多条最短dfs找最优
Dijkstra找最短路径,如果最短路径有多条,存入队列/数组中待用; 然后用dfs遍历各条最短路径,计算每条路径的愉悦值和步数,从中选最优路径
此方法的两个实现:
//转自牛客网牛友提交的代码:
//https://www.nowcoder.com/profile/5832296/codeBookDetail?submissionId=10915168
#include <iostream>
#include <vector>
#include <set>
#include <algorithm>
#include <string>
#include <map>
using namespace std;
#define INF 9999999
struct city{
city(string _n, int _h){name=_n; happy=_h;}
string name;
int happy;
};
vector<city> cities;
vector<vector<int> > cost;
vector<vector<int> > allPath;
vector<int> bestPath;
vector<int> possiblePath;
vector<bool> visited;
vector<int> dist; //记录起点到各个点的距离
map<string, int> name2id;
int cityNum, roadNum;
int cnt = 0;
void dijkstra(int s){
int i;
dist[s] = 0;
while(true){
int v = -1;
for(int u=0; u<cityNum; u++){
if(!visited[u]&&(v==-1||dist[u]<dist[v])) v=u;
}
if(v==-1) break;
visited[v]=true;
for(int u=0; u<cityNum; u++){
if(dist[u] > dist[v] + cost[v][u]){
dist[u] = dist[v] + cost[v][u];
allPath[u].clear();
allPath[u].push_back(v);
}else if(dist[u]==dist[v]+cost[v][u]){
allPath[u].push_back(v);
}
}
}
}
int maxHappy = 0;
double maxAve = 0;
int pathNum = 0; //最短路的条数
void findBestPath(int t){
possiblePath.push_back(t);
if(t==0){
pathNum++;
int happy = 0;
for(int i=0; i<possiblePath.size(); i++){
int index = possiblePath[i];
happy += cities[index].happy;
}
if(happy > maxHappy){
bestPath = possiblePath;
maxHappy = happy;
maxAve = (double)happy/(double)(possiblePath.size()-1);
}else if(happy==maxHappy){
double aveNow = (double)happy/(double)(possiblePath.size()-1);
if(aveNow>maxAve){
bestPath = possiblePath;
maxAve = aveNow;
}
}
return;
}
for(int i=0; i<allPath[t].size(); i++){
findBestPath(allPath[t][i]);
possiblePath.pop_back();
}
}
int main(int argc, char** argv) {
int c, i, j, happy;
string start, from, to, str;
scanf("%d%d",&cityNum, &roadNum);
cin>>start;
cities.push_back(city(start,0));
name2id[start] = 0;//起点
for(i=1; i<cityNum; i++){
cin>>str>>happy;
name2id[str] = i;
cities.push_back(city(str,happy));
}
cost.resize(cityNum, vector<int>(cityNum,INF));
for(i=0; i<roadNum; i++){
cin>>from>>to>>c;
int a = name2id[from];
int b = name2id[to];
cost[a][b] = cost[b][a] = c;
}
dist.resize(cityNum,INF);
for(i=0; i<cityNum; i++)
dist[i] = cost[0][i];
int s = 0;//起点
int t = name2id["ROM"];//终点
visited.resize(cityNum,false);
allPath.resize(cityNum);
dijkstra(s);//查找从起点出发的所有最短路
findBestPath(t);//找到最短路中的最优解
int minCost=0;
for(i=bestPath.size()-1; i>0; i--){
int a = bestPath[i];
int b = bestPath[i-1];
minCost += cost[a][b];
}
cout<<pathNum<<" "<<minCost<<" "<<maxHappy<<" "<<(int)maxAve<<endl;
for(i=bestPath.size()-1; i>=0; i--){
string name = cities[bestPath[i]].name;
if(i!=0)
cout<<name<<"->";
else
cout<<name<<endl;
}
return 0;
}
另一个相似实现
//转自牛客网牛友提交的代码
//https://www.nowcoder.com/profile/7316467/codeBookDetail?submissionId=9006304
#include<iostream>
#include<vector>
#include<string>
#include<map>
#define INF 0x3f3f3f3f
using namespace std;
struct City
{
int Position, Happy;
};
City cst_cty(int happy, int position) {
City new_city;
new_city.Happy = happy;
new_city.Position = position;
return new_city;
}
void dfs(int cur, vector<bool>& vis, vector<vector<int>>& pre, vector<int>& path, double& max_avg, int& max_happiness,int end,int temp_hap, map<int, string>& pos_name, map<string, City>& name_info, vector<int>& temp_path) {
vis[cur] = true;
temp_path.push_back(cur);
//temp_hap += name_info[pos_name[cur]].Happy;
if (cur==end)
{
int temp_hap = 0;
for (int i = 0; i < int(temp_path.size()); i++)
{
int cur = temp_path[i];
temp_hap += name_info[pos_name[cur]].Happy;
}
double temp_avg = temp_hap*1.0 / (temp_path.size() - 1);
if (temp_hap>max_happiness)
{
max_happiness = temp_hap;
path = temp_path;
max_avg = temp_avg;
}
else if (temp_hap==max_happiness&&temp_avg>max_avg)
{
max_avg = temp_avg;
path = temp_path;
}
}
for (vector<int>::iterator it = pre[cur].begin(); it != pre[cur].end(); it++)
{
//if (vis[*it]==false)
//{
dfs(*it, vis, pre, path, max_avg, max_happiness, end, temp_hap, pos_name, name_info, temp_path);
//}
}
//temp_hap -= name_info[pos_name[cur]].Happy;
temp_path.pop_back();
}
int main() {
int N, K;
string start;
cin >> N >> K >> start;
map<string, City> name_info;
map<int, string> pos_name;
name_info[start] = cst_cty(0, 0);
pos_name[0] = start;
for (int i = 1; i < N; i++)
{
int temp_happy;
string temp_name;
cin >> temp_name >> temp_happy;
name_info[temp_name] = cst_cty(temp_happy, i);
pos_name[i] = temp_name;
}
vector<vector<int>> mat(N, vector<int>(N, 0));
for (int i = 0; i < K; i++)
{
string name_a, name_b;
int cost;
cin >> name_a >> name_b >> cost;
mat[name_info[name_a].Position][name_info[name_b].Position] = mat[name_info[name_b].Position][name_info[name_a].Position] = cost;
}
//初始化
//djk
vector<vector<int>> pre(N, vector<int>());//记录最短路径的自终点开始的前驱节点
vector<int> dis(N, INF);
vector<bool> vis(N, false);
int start_cty = name_info[start].Position, end_cty = name_info["ROM"].Position;
dis[start_cty] = 0;//dis[i]记录起始点到i点的最短距离
vector<int> path_cnt(N, 0);
path_cnt[start_cty] = 1;
while (true)
{
int cur_node = -1, min_dis = INF;
for (int i = 0; i < N; i++)
{
if (vis[i]==false&&dis[i]<min_dis)
{
min_dis = dis[i];
cur_node = i;
}
}//找到当前情况下既没有访问过同时又离起始节点距离最小的节点
//if (min_dis == INF || cur_node == end_cty)
if (cur_node==-1)
{
break;
}
//min_dis为无穷表示找不到最小的边
vis[cur_node] = true;
for (int i = 0; i < N; i++)
{
if (vis[i]==false&&mat[cur_node][i]>0)//考察离起始点最近的节点相连的节点是否需要更新
{
if (dis[i]>dis[cur_node]+mat[cur_node][i])
{
dis[i] = dis[cur_node] + mat[cur_node][i];
pre[i].clear();
pre[i].push_back(cur_node);
path_cnt[i] = path_cnt[cur_node];
}
else if (dis[i]==dis[cur_node]+mat[cur_node][i])//不能写成if,否则前面修改了dis[i]之后,后面必然是相等的,这样,两个if语句都会执行
{
pre[i].push_back(cur_node);
path_cnt[i] += path_cnt[cur_node];
}
}
}
}
//pre记录前驱节点,然后使用dfs从终点逆序遍历
//dfs部分
vector<int> temp_path, path;
int max_happiness = 0;
double max_avg = 0.0;
dfs(end_cty, vis, pre, path, max_avg, max_happiness, start_cty, 0, pos_name, name_info, temp_path);
cout << path_cnt[end_cty] << " " << dis[end_cty] << " " << max_happiness << " " << int(max_avg) << endl;
cout << pos_name[start_cty];
for (int i = int(path.size()-2); i >= 0; i--)
{
cout << "->" << pos_name[path[i]];
}
return 0;
}
方法3:DFS加剪枝
//链接:https://www.nowcoder.com/questionTerminal/bf8045decb1348a3bd6967305cbdad4c
//来源:牛客网——牛客156003592号的讨论代码
#include <cstdio>
#include <iostream>
#include <queue>
#include <utility>
#include <string>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
map<string, int> to_id;
map<int, string> to_name;
vector<int> hps(200);
vector<vector<pair<int, int>>> graph(200);
vector<bool> visited(200);
vector<int> path;
vector<int> ans;
int min_cost = INF;
int max_hp = -INF;
int avg_hp = -INF;
int diff_cnt = 0;
void dfs(int curr, int cost, int hp){
visited[curr] = true;
path.push_back(curr);
if(curr == to_id[string("ROM")]){
if(cost < min_cost){
min_cost = cost;
max_hp = hp;
avg_hp = hp / (path.size() - 1);
diff_cnt = 1;
ans = path;
}
else{
diff_cnt++;
if(hp > max_hp){
max_hp = hp;
avg_hp = hp / (path.size() - 1);
ans = path;
}
else if(hp == max_hp){
if((int) (hp / (path.size() - 1)) > avg_hp){
avg_hp = hp / (path.size() - 1);
ans = path;
}
}
}
}
for(auto& p : graph[curr]){
int to = p.first;
int c = p.second;
if(visited[to]) continue;
if(cost + c > min_cost) continue;
dfs(to, cost + c, hp + hps[to]);
}
visited[curr] = false;
path.pop_back();
}
int main(){
ios::sync_with_stdio(false);
int N, K;
string start;
cin >> N >> K >> start;
to_id[start] = 0;
to_name[0] = start;
for(int i = 1; i <= N - 1; i++){
string city;
int hp;
cin >> city >> hp;
to_id[city] = i;
to_name[i] = city;
hps[i] = hp;
}
for(int i = 0; i < K; i++){
string city1, city2;
int from, to, cost;
cin >> city1 >> city2 >> cost;
from = to_id[city1];
to = to_id[city2];
graph[from].emplace_back(to, cost);
graph[to].emplace_back(from, cost);
}
dfs(0, 0, 0);
cout << diff_cnt << " " << min_cost << " ";
cout << max_hp << " " << avg_hp << endl;
for(int i = 0; i < (int)ans.size(); i++){
if(i) cout << "->";
cout << to_name[ans[i]];
}
cout << endl;
}
总感觉这位牛友diff_cnt++;这句代码应该加个判断是不是cost相等。但是人家的代码通过了,amazing。
排序问题
例1
插入还是堆排序
给原始序列、排序排到一半的序列。问排序方法是插入排序还是堆排序。然后要求给出下一步的排序结果
两种排序的区别: 插入排序前面部分是排好的,后面的部分没有改变(稳定的排序) 堆排序后面部分是排好的,前面部分也发生了改变(不稳定) 可根据以上两种排序的特点确定是堆排序还是插入排序。
注意插入排序和堆排序的排序过程,继续排一步
题解
package com.jingmin.advanced2;
import java.util.Scanner;
/**
* @author : wangjm
* @date : 2020/6/1 10:25
* @discription: https://www.nowcoder.com/pat/5/problem/4322
* 插入排序、堆排序
*/
public class Advanced1009 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] a = new int[n];
int[] b = new int[n];
for (int i = 0; i < n; i++) {
a[i] = scanner.nextInt();
}
for (int i = 0; i < n; i++) {
b[i] = scanner.nextInt();
}
StringBuilder sb = new StringBuilder();
//如果是插入排序,返回的是一个大于0的数(已排序个数)
int insertionSortLength = insertionSortLength(a, b);
sb.append(insertionSortLength > 0 ? "Insertion Sort" : "Heap Sort").append("\n");
if (insertionSortLength > 0) {
//如果是插入排序,继续排一步
nextInsertionSort(b, insertionSortLength);
} else {
//如果是堆排序,确定排到哪个位置了(pos是堆尾)
int pos = heapSortNextPos(a, b);
if (pos > 0) {
//继续排一步
nextHeapSort(b, pos);
}
}
for (int i = 0; i < n; i++) {
sb.append(b[i]).append(" ");
}
sb.setLength(sb.length() - 1);
System.out.println(sb);
scanner.close();
}
private static int insertionSortLength(int[] a, int[] b) {
int i = 1;
while (i < b.length && b[i] >= b[i - 1]) {
i++;
}
int j = i;
while (j < b.length && a[j] == b[j]) {
j++;
}
if (j != b.length) {
i = 0;
}
return i;
}
private static int heapSortNextPos(int[] a, int[] b) {
int i = b.length - 2;
while (i >= 0 && b[i] <= b[i + 1]) {
i--;
}
int max = -1;
for (int j = 0; j <= i; j++) {
if (b[j] > max) {
max = b[j];
}
}
while (max > b[i + 1]) {
i++;
}
return i;
}
private static void nextInsertionSort(int[] b, int pos) {
int tmp = b[pos];
int i = pos - 1;
while (i >= 0 && b[i] > tmp) {
b[i + 1] = b[i];
i--;
}
b[++i] = tmp;
}
private static void nextHeapSort(int[] b, int pos) {
//交换堆顶和堆尾,堆size--,从堆顶向下调整
int tmp = b[0];
b[0] = b[pos];
b[pos] = tmp;
adjust(b, 0, pos);
}
/**
* 堆排序的整体过程(这里只是方便参考,本题中没有用到)
*/
/* private static void heapSort(int[] a) {
//初始化堆:从第一个非叶子节点开始向前,每一个节点和其子节点进行递归调整
int size = a.length;
for (int i = (a.length - 1) / 2; i >= 0; i--) {
adjust(a, i, size);
}
//交换堆顶和堆尾,堆大小-1,从堆顶向下调整;重复直到堆变为空
while (size > 0) {
//交换
int tmp = a[size - 1];
a[size - 1] = a[0];
a[0] = tmp;
//堆size--,从堆顶向下调整
adjust(a, 0, --size);
}
}*/
/**
* 递归调整当前节点与其子节点
* 可以优化为非递归形式(未实现)
*/
private static void adjust(int[] heap, int pos, int heapSize) {
int left = pos * 2 + 1;
int right = pos * 2 + 2;
//找节点与其子节点中最大值的节点下标
int max = (left < heapSize && heap[left] > heap[pos]) ? left : pos;
max = (right < heapSize && heap[right] > heap[max]) ? right : max;
if (max != pos) {
//调整/交换
int tmp = heap[pos];
heap[pos] = heap[max];
heap[max] = tmp;
//递归调整子节点
adjust(heap, max, heapSize);
}
}
}
动态规划
动态规划思想可以用来解决最优化问题。
最优化问题的形式 max/min 目标函数F() st. 限制条件(等式、不等式、变量范围限制)
最长不下降子序列
最长子序列长度问题的介绍,在算法总结.md#动态规划
例1 最长的可接受花色条纹子序列
给一个序列,表示可接受的花色序列。再给一个序列,表示已有的花色序列。要从已有的花色序列中裁取可接受的花色序列(每种可接受的花色可保留多份)。
比如已有的花色序列是 {2 2 4 1 5 5 6 3 1 1 5 6}. 可接受的花色序列是{2 3 1 5 6},
那么有如下的裁取方式{2 2 1 1 1 5 6}, {2 2 1 5 5 5 6}, {2 2 1 5 5 6 6}, 和 {2 2 3 1 1 5 6}.
方法1 映射法 转换为最长不下降子序列长度问题
参考:https://www.nowcoder.com/questionTerminal/0171de2cf94a43d690c336a363a41693
建立映射表 (2,1) (3,2) (1,3) (5,4) (6,5)
初始条带
2 2 4 1 5 5 6 3 1 1 5 6 将条带中不存在的颜色去掉 2 2 1 5 5 6 3 1 1 5 6 根据映射表,对条带进行映射: 1 1 3 4 4 5 2 3 3 4 5 问题转换为求最长不下降子序列
package com.jingmin.advanced2;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
/**
* @author : wangjm
* @date : 2020/6/20 23:19
* @discription : https://www.nowcoder.com/pat/5/problem/4084
* 将eva喜欢的颜色按顺序编号(赋权),建立映射关系(颜色-编号)。
* 将条带中不符合eva喜好的颜色去掉。根据映射关系生成剩余条带的编号序列。
* 则原题目变成:求剩余条带编号的最长不下降子序列长度。
*/
public class Advanced1034 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
Map<Integer, Integer> map = new HashMap<>(20);
for (int i = 1; i <= m; i++) {
map.put(scanner.nextInt(), i);
}
int l = scanner.nextInt();
int[] a = new int[l];
int count = 0;
for (int i = 0; i < l; i++) {
Integer tmp = map.get(scanner.nextInt());
if (tmp != null) {
a[count++] = tmp;
}
}
scanner.close();
//dp[i]表示以a[i]结尾的最长不下降子序列长度
int[] dp = new int[count];
//边界条件:dp[i] = 1;
//状态转移方程: dp[i] = max(dp[j]+1,dp[i]) , j = 0,1,,i-1, 当[j] <= a[i],
// dp[i] = dp[i], 当所有a[j]都 > a[i]
for (int i = 0; i < count; i++) {
dp[i] = 1;
}
int max = 0;
for (int i = 1; i < count; i++) {
for (int j = 0; j < i; j++) {
if (a[j] <= a[i] && dp[j] + 1 > dp[i]) {
dp[i] = dp[j] + 1;
}
}
max = dp[i] > max ? dp[i] : max;
}
System.out.println(max);
}
}
方法2 其他动态规划法
package com.jingmin.advanced2;
import java.util.Scanner;
/**
* @author : wangjm
* @date : 2020/6/20 23:19
* @discription : https://www.nowcoder.com/pat/5/problem/4084
* 动态规划思想
*/
public class Advanced1034_2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] a = new int[m + 1];
for (int i = 1; i <= m; i++) {
a[i] = scanner.nextInt();
}
int l = scanner.nextInt();
int[] b = new int[l + 1];
for (int i = 1; i <= l; i++) {
b[i] = scanner.nextInt();
}
scanner.close();
//dp[i][j]表示,加入第i种颜色后,前j个颜色序列组成的最大非逆子序列长度
int[][] dp = new int[m + 1][l + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= l; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
if (a[i] == b[j]) {
dp[i][j] += 1;
}
}
}
System.out.println(dp[m][l]);
}
}
背包问题
如果背包问题还不太了解,可以参考:算法笔记——胡凡曾磊 (P444 提高篇(5)动态规划专题) 背包问题进阶:背包九讲
01背包问题
01背包问题是这样的:有n件物品,每件物品的重量w[i],价值c[i]。现有一个背包,容量为V,问如何选择物品装入背包,使装入背包物品的总价值最大?
例1 用零钱凑一定的金额
给n张零钱,面值分别为v[i],问如何选择零钱,凑成给定的金额V。如果有多种方法,使用面值尽量小的,张数多的方法。
这道题目属于:背包问题-01背包问题-01满背包问题
从最优化问题的角度考虑,
可以看作是如下的最优化问题(方法1):
限制条件: 变量i 属于[1,n], 面值v[i] 属于{v[1]:v[n]} 选择的面值之和必须恰好为给定的金额V 目标函数: 使用的零钱张数(最多)
也可以看作是如下的最优化问题(方法2):
限制条件: 变量i 属于[1,n], 面值v[i] 属于{v[1]:v[n]} 选择的零钱总额小于等于给定的金额V 目标函数: 使用的零钱总额(最大)
方法1 凑给定金额V,使用的零钱张数最大
假设第i张零钱的面值是$v[i]$ 。用$dp[i][v]$表示从前i张零钱中,凑成金额v时的零钱张数。
考虑是否选择第i张零钱(凑成金额v,使用的零钱张数最大)
如果选择使用第i张零钱凑成金额v,使用的零钱张数$dp[i][v]$由前$i-1$张零钱使用的张数决定,即$dp[i][v] = dp[i-1][v-v[i]]+1$ 如果选择不使用第i张零钱凑成金额v,使用的零钱张数$dp[i][v]$也由前$i-1$张零钱使用的张数决定,即$dp[i][v] = dp[i-1][v]$ 最终是否使用第i张零钱凑成金额v,选以上两种方式中,使用零钱张数较多的一种,即$dp[i][v] = max(dp[i-1][v-v[i]]+1, dp[i-1][v])$
关于初始化
$dp[1:n][1:n]$全都初始化为了-inf (也可以是其他特定的数值),表示不能从这些位置开始转移。$dp[1:n][0]$全部初始化为0,是状态转移方程的边界(起始位置)
最终$dp[n][V]$表示恰好凑成金额V所使用的零钱张数
java代码
package com.jingmin.advanced2;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
/**
* @author : wangjm
* @date : 2020/6/13 18:21
* @discription : https://www.nowcoder.com/pat/5/problem/4119
* 最优化问题:动态规划问题:选硬币问题,满背包问题
* <p>
* 最优化问题描述
* 目标函数:使用零钱张数最多
* 限制条件:使用的面值之和为V
* <p>
* 动态规划将最优化问题分解为多个子问题,通过综合子问题的最优解来得到原问题的最优解。且动态规划会将子问题的解保存下来,避免重复计算
* 动态规划问题的状态转移方程:
* dp[i][v] = max(dp[i-1][v-v[i]]+1, dp[i-1][v])
* 使用第i张零钱凑成金额v,或不使用第i张零钱凑成金额v,使用的零钱张数dp[i][v]都和前i-1张零钱的使用状况有关。是否使用第i张,取决于哪种情况使用的零钱张数多。
*/
public class Advanced1026 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] coins = new int[n + 1];
for (int i = 1; i <= n; i++) {
coins[i] = scanner.nextInt();
}
scanner.close();
//排序,逆序
Arrays.sort(coins);
for (int i = 1, j = n; i < j; i++, j--) {
int tmp = coins[i];
coins[i] = coins[j];
coins[j] = tmp;
}
//背包数组,记录存入背包的硬币个数;路径记录数组
int[][] dp = new int[n + 1][m + 1];
boolean[][] flag = new boolean[n + 1][m + 1];
//默认初始化dp[1:n][0]为0,dp[1:n][1:m]设为-1表示不能从这些位置开始转移。
for (int i = 0; i <= n; i++) {
for (int j = 1; j < dp[i].length; j++) {
dp[i][j] = -1;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
dp[i][j] = dp[i - 1][j];
//恰好装满的判断:保证不是从-1转移过来的
if ((j - coins[i] >= 0) && (dp[i - 1][j - coins[i]] != -1)) {
if (dp[i - 1][j - coins[i]] + 1 >= dp[i][j]) {
dp[i][j] = dp[i - 1][j - coins[i]] + 1;
flag[i][j] = true;
}
}
}
}
if (dp[n][m] != -1) {
int i = n;
int j = m;
ArrayList<Integer> list = new ArrayList<>();
while (i > 0 && j > 0) {
if (flag[i][j]) {
list.add(coins[i]);
j -= coins[i];
}
i--;
}
StringBuilder sb = new StringBuilder();
for (Integer e : list) {
sb.append(e).append(" ");
}
sb.setLength(sb.length() - 1);
System.out.println(sb);
} else {
System.out.println("No Solution");
}
}
}
java代码优化(降为1维数组/滚动数组)
原来的动态规划问题的状态转移方程:
$dp[i][v] = max(dp[i-1][v-v[i]]+1, dp[i-1][v])$
使用第i张零钱凑成金额v,或不使用第i张零钱凑成金额v,使用的零钱张数dp[i][v]都和前i-1张零钱的使用状况有关。是否使用第i张,取决于哪种情况使用的零钱张数多。
优化:
由于使用的零钱张数dp[i][v]都仅和前i-1张零钱的使用状况$dp[i-1][1:v]$有关,我们可以将2维数组降为1维数组(滚动数组)
新的状态转移方程:
$dp[v] = max(dp[v-v[i]]+1, dp[v])$
由于dp[v-v[i]]+1, dp[v]使用的是上一轮(i-1轮)的值,在dp[v]使用前不应当被更改,所以对v的枚举应该逆序进行。
package com.jingmin.advanced2;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
/**
* @author : wangjm
* @date : 2020/6/13 18:21
* @discription : https://www.nowcoder.com/pat/5/problem/4119
* 最优化问题:动态规划问题:选硬币问题,满背包问题
* <p>
* 最优化问题描述
* 目标函数:使用零钱张数最多
* 限制条件:使用的面值之和恰好为V
* <p>
* 动态规划将最优化问题分解为多个子问题,通过综合子问题的最优解来得到原问题的最优解。且动态规划会将子问题的解保存下来,避免重复计算
* 动态规划问题的状态转移方程:
* dp[i][v] = max(dp[i-1][v-v[i]]+1, dp[i-1][v])
* 使用第i张零钱凑成金额v,或不使用第i张零钱凑成金额v,使用的零钱张数dp[i][v]都和前i-1张零钱的使用状况有关。是否使用第i张,取决于哪种情况使用的零钱张数多。
* <p>
* 优化:
* 由于使用的零钱张数dp[i][v]都仅和前i-1张零钱的使用状况dp[i-1][1:v]有关,我们可以将2维数组降为1维数组(滚动数组)
* 新的状态转移方程:
* dp[v] = max(dp[v-v[i]]+1, dp[v])
* 由于dp[v-v[i]]+1, dp[v]使用的是上一轮(i-1轮)的值,在dp[v]使用前不应当被更改,所以对v的枚举应该逆序进行。
*/
public class Advanced1026_2 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] coins = new int[n + 1];
for (int i = 1; i <= n; i++) {
coins[i] = scanner.nextInt();
}
scanner.close();
//排序,逆序
Arrays.sort(coins);
for (int i = 1, j = n; i < j; i++, j--) {
int tmp = coins[i];
coins[i] = coins[j];
coins[j] = tmp;
}
//背包数组,记录存入背包的硬币个数;路径记录数组
int[] dp = new int[m + 1];
boolean[][] flag = new boolean[n + 1][m + 1];
//默认初始化dp[0]为0,dp[1:m]设为-1表示不能从这些位置开始转移。
for (int j = 1; j <= m; j++) {
dp[j] = -1;
}
for (int i = 1; i <= n; i++) {
for (int j = m; j >= coins[i]; j--) {
//恰好装满的判断:保证不是从-1转移过来的
if (dp[j - coins[i]] != -1) {
if (dp[j - coins[i]] + 1 >= dp[j]) {
dp[j] = dp[j - coins[i]] + 1;
flag[i][j] = true;
}
}
}
}
if (dp[m] != -1) {
int i = n;
int j = m;
ArrayList<Integer> list = new ArrayList<>();
while (i > 0 && j > 0) {
if (flag[i][j]) {
list.add(coins[i]);
j -= coins[i];
}
i--;
}
StringBuilder sb = new StringBuilder();
for (Integer e : list) {
sb.append(e).append(" ");
}
sb.setLength(sb.length() - 1);
System.out.println(sb);
} else {
System.out.println("No Solution");
}
}
}
方法2 使用的零钱面值总额不超过V,使得使用的零钱面值总额最大
如果目标函数(使用的零钱总额)最大值就是V,那么原问题(用零钱凑给定金额V)有解。
//牛客网牛友bystc提交的代码
//https://www.nowcoder.com/profile/5065450/codeBookDetail?submissionId=12502427
#include <cstdio>
#include <cmath>
#include <algorithm>
const int ncoins = 10005;
const int nmonay = 105;
bool cmp(const int &a, const int &b) {
return a > b;
}
int main() {
int dp[ncoins][nmonay];
int coins[ncoins];
bool isIncluded[nmonay][ncoins];
int n, m;
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; ++i) {
scanf("%d", &coins[i]);
}
std::sort(coins + 1, coins + n + 1, cmp);
for(int i = 1; i <= m; ++i)
for(int j = 1; j <= n; ++j)
isIncluded[i][j] = false;
for(int i = 0; i <= m; ++i) dp[0][i] = 0;
for(int i = 0; i <= n; ++i) dp[i][0] = 0;
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j) {
if( j < coins[i] || dp[i - 1][j] > coins[i] + dp[i - 1][j - coins[i]] ) {
dp[i][j] = dp[i - 1][j];
}
else {
dp[i][j] = dp[i - 1][j - coins[i]] + coins[i];
isIncluded[j][i] = true;
}
}
if(dp[n][m] != m) {
printf("No Solution\n");
return 0;
}
bool flag = true;
for(int i = n; i >= 1 && m > 0; --i) {
if(isIncluded[m][i]) {
if(flag) {
printf("%d", coins[i]);
flag = false;
}
else
printf(" %d", coins[i]);
m -= coins[i];
}
}
printf("\n");
return 0;
}
初始化的问题
不同的初始化条件决定了dp数组的意义: 是装入的总价值的最大值(不一定恰好装满) 还是装入的总价值(但一定装满)
具体的讲,初始化的问题(可用数学归纳法证明状态的转移过程:见bilibili大雪菜背包九讲专题):
对于滚动数组/一维数组,$dp[0:m]$都初始化为0,则$dp[m]$中表示的内容,就是背包里装入物品总价值的最大值(背包不一定装满) 对于滚动数组/一维数组,$dp[1:m]$都初始化为$-INF$,$dp[0] = 0$, 则$dp[m$]中表示的内容,就是(恰好装满背包容量m时)背包里物品的总价值 对于二维数组,$dp[0:n][0:m]$都初始化为0,则$dp[n][m]$中表示的内容,就是背包里装入物品总价值的最大值(背包不一定装满) 对于二维数组,$dp[0:n][1:m]$都初始化为$-INF$,$dp[1:n][0] = 0$, 则$dp[n][m]$中表示的内容,就是(恰好装满背包容量m时)背包里物品的总价值